
一、课程的地位与作用 《常微分方程》是数学专业及相关专业的重要基础课之一,是数学的一个重要分支,也 是数学理论联系实际的重要渠道之一。它对先行课(数学分析与高等代数)及后续课(微分 方程数值解、数学物理方程等)起到承前启后的作用,是数学理论中不可缺少的一个环节, 对训练学生分析问题和解决问题的能力起重要作用。通过本课程的学习,使学生正确理解常 微分方程的基本概念,掌握基本理论和主要方法,培养学生理论联系实际的意识和能力,为 后续的数学和应用数学各课程准备解决问题的方法和工具。 二、课程对应的毕业要求 通过该课程的学习得到良好的数学训练,并具有扎实的数学基础和严密的逻辑思维能力 通过该课程学习,针对复杂工程问题,能够理解和评价工程实际对自然环境、社会环境以及 可持续发展的影响。培养具有自主学习和终身学习的意识,有不断学习和适应发展的能力。 三、课程教学目标 通过本课程的学习,使学生掌握使用初等积分法求解变量分离方程、齐次方程、一阶线 性微分方程、全微分方程、一阶隐式微分方程、几种可降阶的高阶方程,掌握解的存在唯 性理论,熟练掌握线性微分方程(组)的基本理论和求解方法,理解常微分方程稳定性的基 本理论,使学生受到科研的初步训练。 四、课程教学内容提要与基本要求 理论部分 序号 教学内容提要 基本要求 学时 第一章初等积分法 理解有关微分方程的基本概念,初步学 1.1微分方程与解 握变量可分离方程及齐次方程的解法: 12变量可分离方程(一) 12变量可分离方程(二) 掌握一阶线性方程及贝努力方程的解 法:理解积分因子在求解微分方程中的 13齐次方程 阶线性方程 作用,掌握全微分方程的解法 1 了解方向场和积分曲线的关系 掌握克 15全微分方程及积分因子 16 莱洛方程的解法:掌握一阶隐式方程的 16线素场与欧拉折线 17一阶隐式微分方程(一) 参数表示及通解求法,建立常微分方程 解决简单的几何、物理问题。 17一阶隐式微分方程(二) 18一阶微分方程应用举例( 掌握通过建立常微分方程解决简单的几 阶微分方程应用举例 可 物理问题的方法 掌握三种常见的 可降阶的高阶方程的解法 1.9几种可降阶的高阶方程 第二章基本理论 理解右端函数连续保证初值问题解的存 2.1解的存在性与唯一性定理 在性,李普希茨条件保证初值问题解的 2 4 2.2解的延展 唯一性。掌握用毕卡逐次逼近法证明 2.3解对初值的连续依赖性 阶常微分方程初值问题解的存在唯一性
16 一、课程的地位与作用 《常微分方程》是数学专业及相关专业的重要基础课之一,是数学的一个重要分支,也 是数学理论联系实际的重要渠道之一。它对先行课(数学分析与高等代数)及后续课(微分 方程数值解、数学物理方程等)起到承前启后的作用,是数学理论中不可缺少的一个环节, 对训练学生分析问题和解决问题的能力起重要作用。通过本课程的学习,使学生正确理解常 微分方程的基本概念,掌握基本理论和主要方法,培养学生理论联系实际的意识和能力,为 后续的数学和应用数学各课程准备解决问题的方法和工具。 二、课程对应的毕业要求 通过该课程的学习得到良好的数学训练,并具有扎实的数学基础和严密的逻辑思维能力, 通过该课程学习,针对复杂工程问题,能够理解和评价工程实际对自然环境、社会环境以及 可持续发展的影响。培养具有自主学习和终身学习的意识,有不断学习和适应发展的能力。 三、课程教学目标 通过本课程的学习,使学生掌握使用初等积分法求解变量分离方程、齐次方程、一阶线 性微分方程、全微分方程、一阶隐式微分方程、几种可降阶的高阶方程,掌握解的存在唯一 性理论,熟练掌握线性微分方程(组)的基本理论和求解方法,理解常微分方程稳定性的基 本理论,使学生受到科研的初步训练。 四、课程教学内容提要与基本要求 理论部分 序号 教学内容提要 基本要求 学时 1 第一章 初等积分法 1.1 微分方程与解 1.2 变量可分离方程(一) 1.2 变量可分离方程(二) 1.3 齐次方程 1.4 一阶线性方程 1.5 全微分方程及积分因子 1.6 线素场与欧拉折线 1.7 一阶隐式微分方程(一) 1.7 一阶隐式微分方程(二) 1.8 一阶微分方程应用举例(一) 1.8 一阶微分方程应用举例(二) 1.9 几种可降阶的高阶方程 理解有关微分方程的基本概念,初步掌 握变量可分离方程及齐次方程的解法; 掌握一阶线性方程及贝努力方程的解 法;理解积分因子在求解微分方程中的 作用,掌握全微分方程的解法 了解方向场和积分曲线的关系,掌握克 莱洛方程的解法;掌握一阶隐式方程的 参数表示及通解求法,建立常微分方程 解决简单的几何、物理问题。 掌握通过建立常微分方程解决简单的几 何、物理问题的方法,掌握三种常见的 可降阶的高阶方程的解法 16 2 第二章 基本理论 2.1 解的存在性与唯一性定理 2.2 解的延展 2.3 解对初值的连续依赖性 理解右端函数连续保证初值问题解的存 在性,李普希茨条件保证初值问题解的 唯一性。掌握用毕卡逐次逼近法证明一 阶常微分方程初值问题解的存在唯一性 4
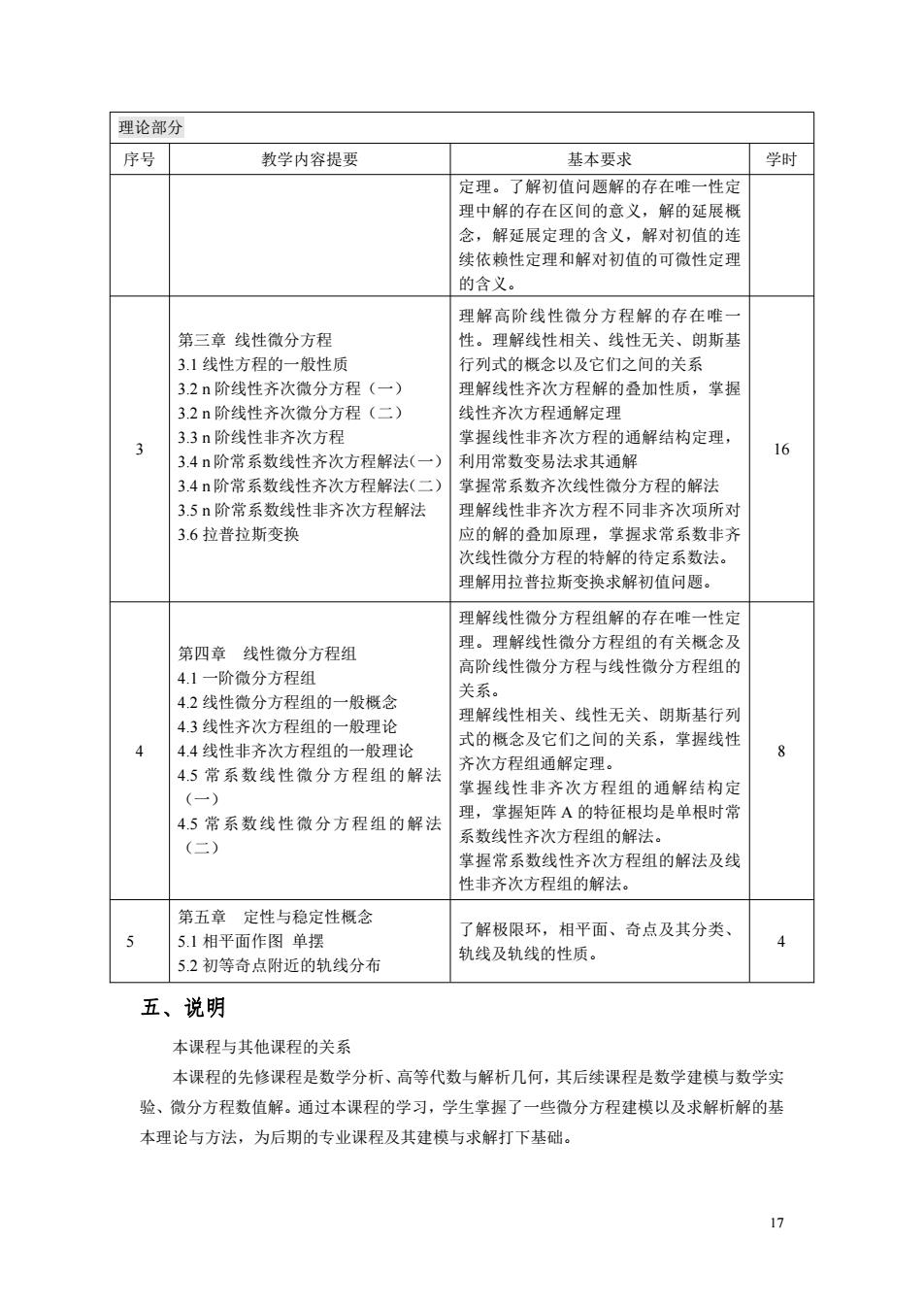
理论部分 序号 教学内容提要 基本要求 学时 定理。了解初值问题解的存在唯一性 理中解的存在区间的意义,解的延展概 念,解延展定理的含义,解对初值的连 续依赖性定理和解对初值的可微性定理 的含义。 理解高阶线性微分方程解的存在雌 第三章线性微分方程 性。理解线性相关、线性无关 朗斯基 3.1线性方程的一般性质 行列式的念以及它们之间的关系 3.2n阶线性齐次微分方程(一) 理解线性齐次方程解的叠加性质,掌握 3.2n阶线性齐次微分方程(二) 线性客次方程铺解定理 33n阶线性非齐次方程 堂挥线性非齐次方程的通解结构定理】 3 3.4n阶常系数线性齐次方程解法( 利用常数变易法求其通解 16 3.4n阶常系数线性齐次方程解法(二 掌握常系数齐次线性微分方程的解法 3.5n阶常系数线性非齐次方程解法 理解线性非齐次方程不同非齐次项所利 3.6拉普拉斯变换 应的解的叠加原理,掌挥求常系数非 次线性微分方程的特解的待定系数法。 理解用拉普拉斯变换求解初值问题。 理解线性微分方程组解的存在唯一性定 第四章线性微分方程组 理。理解线性微分方程组的有关概念及 高阶线性微分方程与线性微分方程组的 4.1一阶微分方程组 关系。 4.2线性微分方程组的一般概念 理解线性相关、线性无关、朝斯基行列 43线性客次方程组的一船理论 4 44线性非齐次方 程组的 般理论 式的概念及它们之间的关系,掌握线性 4.5常系数线性微分方程组的解法 齐次方程组通解定理。 掌握线性非齐次方程组的通解结构园 4.5常系数线性微分方程组的解法 理,掌握矩阵A的特征根均是单根时常 系数线性齐次方程组的解法 (=) 掌握常系数线性齐次方程组的解法及线 性非齐次方程组的解法。 第五章定性与稳定性概念 了解极限环,相平面、奇点及其分类、 5.1相半面作图单摆 4 轨线及轨线的性质。 5.2初等奇点附近的轨线分布 五、说明 本课程与其他课程的关系 本课程的先修课程是数学分析、高等代数与解析几何,其后续课程是数学建模与数学实 验、微分方程数值解。通过本课程的学习,学生掌握了一些微分方程建模以及求解析解的基 本理论与方法,为后期的专业课程及其建模与求解打下基础
17 理论部分 序号 教学内容提要 基本要求 学时 定理。了解初值问题解的存在唯一性定 理中解的存在区间的意义,解的延展概 念,解延展定理的含义,解对初值的连 续依赖性定理和解对初值的可微性定理 的含义。 3 第三章 线性微分方程 3.1 线性方程的一般性质 3.2 n 阶线性齐次微分方程(一) 3.2 n 阶线性齐次微分方程(二) 3.3 n 阶线性非齐次方程 3.4 n 阶常系数线性齐次方程解法(一) 3.4 n 阶常系数线性齐次方程解法(二) 3.5 n 阶常系数线性非齐次方程解法 3.6 拉普拉斯变换 理解高阶线性微分方程解的存在唯一 性。理解线性相关、线性无关、朗斯基 行列式的概念以及它们之间的关系 理解线性齐次方程解的叠加性质,掌握 线性齐次方程通解定理 掌握线性非齐次方程的通解结构定理, 利用常数变易法求其通解 掌握常系数齐次线性微分方程的解法 理解线性非齐次方程不同非齐次项所对 应的解的叠加原理,掌握求常系数非齐 次线性微分方程的特解的待定系数法。 理解用拉普拉斯变换求解初值问题。 16 4 第四章 线性微分方程组 4.1 一阶微分方程组 4.2 线性微分方程组的一般概念 4.3 线性齐次方程组的一般理论 4.4 线性非齐次方程组的一般理论 4.5 常系数线性微分方程组的解法 (一) 4.5 常系数线性微分方程组的解法 (二) 理解线性微分方程组解的存在唯一性定 理。理解线性微分方程组的有关概念及 高阶线性微分方程与线性微分方程组的 关系。 理解线性相关、线性无关、朗斯基行列 式的概念及它们之间的关系,掌握线性 齐次方程组通解定理。 掌握线性非齐次方程组的通解结构定 理,掌握矩阵 A 的特征根均是单根时常 系数线性齐次方程组的解法。 掌握常系数线性齐次方程组的解法及线 性非齐次方程组的解法。 8 5 第五章 定性与稳定性概念 5.1 相平面作图 单摆 5.2 初等奇点附近的轨线分布 了解极限环,相平面、奇点及其分类、 轨线及轨线的性质。 4 五、说明 本课程与其他课程的关系 本课程的先修课程是数学分析、高等代数与解析几何,其后续课程是数学建模与数学实 验、微分方程数值解。通过本课程的学习,学生掌握了一些微分方程建模以及求解析解的基 本理论与方法,为后期的专业课程及其建模与求解打下基础

六、学生成绩考核与评定方式 本课程考核方式为闭卷笔试,成绩由平时成绩和考试成绩两部分构成,其中平时成绩占 30%,考试成绩占70% 七、建议教材与参考书 建议教材:东北师范大学数学系微分方程教研室编著,常微分方程,高等教有出版社,1982 年10月第一版,2001年12月第23次印刷. 参考书:1.林武忠等编著,常微分方程(第一版),科学出版社,2003.9。 2.丁同仁等编著,常微分方程教程(第二版),高等教有出版社,2004.7。 3.庄万主编,常微分方程习题解,山东科学技术出版社2005.1。 八、课程中英文简介 微分方程是数学专业及相关专业的重要基础课之一,是数学的一个重要分支,也是数学 理论联系实际的重要渠道之一,是数学理论中不可缺少的一个环节,对训练学生分析问题和 解决问题的能力起重要作用。通过本课程的学习,使学生正确理解常微分方程的基本概念, 掌握一些特殊方程(比如:变量可分离、齐次方程、隐式方程、一(二)阶线性微分方程(组), 解的存在唯一性、稳定性等)的基本理论和主要方法,培养学生理论联系实际的意识和能力 为后续的数学和应用数学各课程准备解决问题的方法和工具。 Differential equation is one of the basic courses for mathematics and related professional.It is one of the important channels of combing the mathematical theory with practice.It is an indispensable link in the mathematical theory.It plays an in developing students ability of analyzing and solving problems.By leaming this course,the students can understand the basic concepts of ordinary differential equations,grasp the theory and methods of special equations(for example,Variable separable,Homogeneous equation,implicit equation First(second)-order linear differential equation(s),solution existence and uniqueness,stability etc) It can develop the students'awareness and ability of combining the theory with practice,prepare the tools and methods for subsequent mathematics. 《概率论与数理统计》 课程编号 IBL09406 学分 总学时 64 实验/上机学时实验:0学时,上机:0学时 课程名称 英文名称 Probability Theory and 概率论与数理统计 Mathematical Statistics 课程类别 必修 适用专业 信息与计算科学
18 六、学生成绩考核与评定方式 本课程考核方式为闭卷笔试,成绩由平时成绩和考试成绩两部分构成,其中平时成绩占 30%,考试成绩占 70%。 七、建议教材与参考书 建议教材:东北师范大学数学系微分方程教研室编著,常微分方程,高等教育出版社,1982 年 10 月第一版,2001 年 12 月第 23 次印刷。 参考书:1. 林武忠等编著,常微分方程(第一版),科学出版社,2003.9。 2. 丁同仁等编著,常微分方程教程(第二版),高等教育出版社,2004.7。 3. 庄万主编,常微分方程习题解,山东科学技术出版社,2005.1。 八、课程中英文简介 微分方程是数学专业及相关专业的重要基础课之一,是数学的一个重要分支,也是数学 理论联系实际的重要渠道之一,是数学理论中不可缺少的一个环节,对训练学生分析问题和 解决问题的能力起重要作用。通过本课程的学习,使学生正确理解常微分方程的基本概念, 掌握一些特殊方程(比如:变量可分离、齐次方程、隐式方程、一(二)阶线性微分方程(组), 解的存在唯一性、稳定性等)的基本理论和主要方法,培养学生理论联系实际的意识和能力, 为后续的数学和应用数学各课程准备解决问题的方法和工具。 Differential equation is one of the basic courses for mathematics and related professional.It is one of the important channels of combing the mathematical theory with practice. It is an indispensable link in the mathematical theory. It plays an important role in developing students’ ability of analyzing and solving problems. By learning this course, the students can understand the basic concepts of ordinary differential equations, grasp the theory and methods of special equations(for example, Variable separable , Homogeneous equation, implicit equation , First(second)-order linear differential equation(s), solution existence and uniqueness,stability ,etc). It can develop the students’ awareness and ability of combining the theory with practice, prepare the tools and methods for subsequent mathematics. 《概率论与数理统计》 课程编号 1BL09406 学 分 4 总 学 时 64 实验/上机学时 实验:0 学时,上机:0 学时 课程名称 概率论与数理统计 英文名称 Probability Theory and Mathematical Statistics 课程类别 必修 适用专业 信息与计算科学

执笔人 王晶杰 审核人 王爱文 先修课程 数学分析,高等代数 一、课程的地位与作用 概率论与数理统计是信计专业的一门重要基础专业课,该课程是数学理论与实际问题紧 密联系的一门学科。现实世界上事物的联系是非常复杂的,一切事物的发展过程中包含着必 然性的方面,也包含者偶然性的方面,他们是相互对立又相互联系的,而概率论与数理统计 正是研究随机现象统计规律的一门学科。通过本课程的学习,使学生理解随机现象的规律及 特点,掌握利用数学知识解决随机问题的思路和方法,并为后续的相关数学课程(如随机过 程,方差分析等)的学习打下基础。 二、课程对应的毕业要求 通过该课程的学习使学生得到良好的数学训练,能够基于信总与计算科学相关背景知识 进行合理分析,并在多学科环境中得以应用。针对复杂工程问题,能够理解和评价工程实际 对自然环境、社会环境以及可持续发展的影响。能够就数学、计算机科学技术、统计学相关 问题与业界同行及社会公众进行有效沟通和交流,培养具有自主学习和终身学习的意识,有 不断学习和适应发展的能力。 三、课程教学目标 使学生掌握概率论及数理统计中的基本定义,基本定理及主要定理的推导证明,能熟练运 用这些基本概念进行相应的数学运算和论证,了解本课程在实际生活中的应用方向及应用方 法,能对典型实际问题进行建模求解,并将计算结果进行分析后用生活中的语言表达方式进行 阐述,以达到学以致用的效果。 四、课程教学内容提要与基本要求 理论部分 序号 教学内容提要 基本要求 学时 第一章随机事件与概率 11随机事件 介绍集合论的基础知识及概率论中的 基本概念、 1 2事件的关系与运算 熟练掌握古典 3 典型 概型的计算 了解几何概型的计算方 10 1.4几何概型 法,了解概率的公理化定义 15概率的公理化定义 第二章条件概率与独立性 21条件概率。 掌握条件概率的定义及计算,熟练 乘法定理 握乘法定理、全概率公式的原理及计 2.2全概率公式 算方法,了解贝叶斯公式的使用方法 2.3贝叶斯公式 掌握事件独立性的定义及相关计算, 2.4事件的独立性 熟练使用二项概率公式及泊松丽近定 2.5重复独立试验 二项概率公式 理进行计算
19 执 笔 人 王晶杰 审 核 人 王爱文 先修课程 数学分析, 高等代数 一、课程的地位与作用 概率论与数理统计是信计专业的一门重要基础专业课,该课程是数学理论与实际问题紧 密联系的一门学科。现实世界上事物的联系是非常复杂的,一切事物的发展过程中包含着必 然性的方面,也包含着偶然性的方面,他们是相互对立又相互联系的,而概率论与数理统计 正是研究随机现象统计规律的一门学科。通过本课程的学习,使学生理解随机现象的规律及 特点,掌握利用数学知识解决随机问题的思路和方法,并为后续的相关数学课程(如随机过 程,方差分析等)的学习打下基础。 二、课程对应的毕业要求 通过该课程的学习使学生得到良好的数学训练,能够基于信息与计算科学相关背景知识 进行合理分析,并在多学科环境中得以应用。针对复杂工程问题,能够理解和评价工程实际 对自然环境、社会环境以及可持续发展的影响。能够就数学、计算机科学技术、统计学相关 问题与业界同行及社会公众进行有效沟通和交流,培养具有自主学习和终身学习的意识,有 不断学习和适应发展的能力。 三、课程教学目标 使学生掌握概率论及数理统计中的基本定义,基本定理及主要定理的推导证明,能熟练运 用这些基本概念进行相应的数学运算和论证,了解本课程在实际生活中的应用方向及应用方 法,能对典型实际问题进行建模求解,并将计算结果进行分析后用生活中的语言表达方式进行 阐述,以达到学以致用的效果。 四、课程教学内容提要与基本要求 理论部分 序号 教学内容提要 基本要求 学时 1 第一章 随机事件与概率 1.1 随机事件 1.2 事件的关系与运算 1.3 古典概型 1.4 几何概型 1.5 概率的公理化定义 介绍集合论的基础知识及概率论中的 基本概念、基本公式,熟练掌握古典 概型的计算,了解几何概型的计算方 法,了解概率的公理化定义 10 2 第二章 条件概率与独立性 2.1 条件概率,乘法定理 2.2 全概率公式 2.3 贝叶斯公式 2.4 事件的独立性 2.5 重复独立试验,二项概率公式 掌握条件概率的定义及计算,熟练掌 握乘法定理、全概率公式的原理及计 算方法,了解贝叶斯公式的使用方法, 掌握事件独立性的定义及相关计算, 熟练使用二项概率公式及泊松逼近定 理进行计算 8
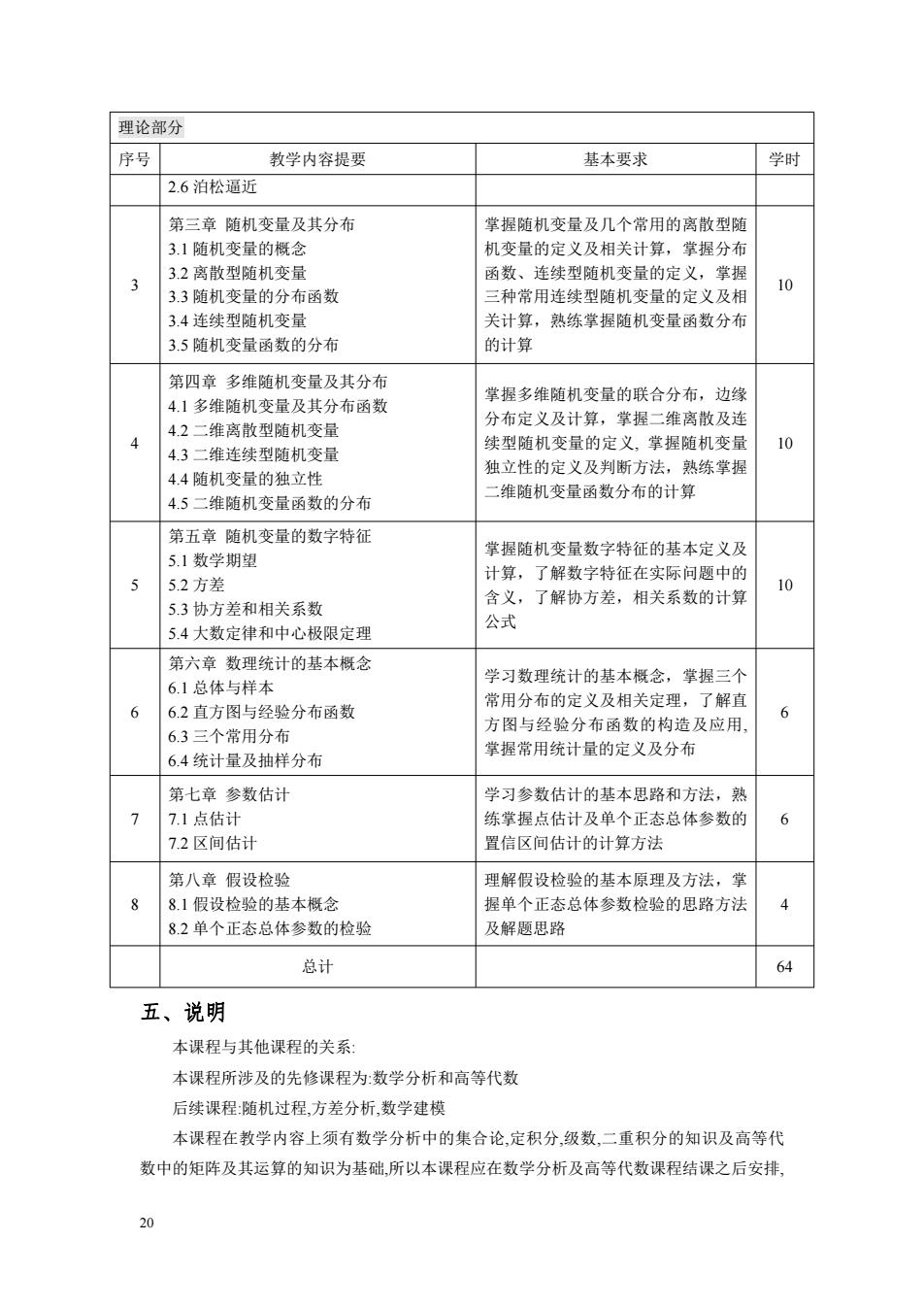
理论部分 序号 教学内容提要 基本要求 学时 2.6泊松逼近 第三章随机变量及其分布 掌握随机变量及几个常用的离散型随 31随机变量的概 机变最的定义及相关计 堂分布 3 函数 连续型随机变量的 三种常用连续型随机变量的定义及相 10 3.4连续型随机变量 关计算,熟练掌握随机变量函数分布 3.5随机变量函数的分布 的计算 第四音多维随机弯量及其分在 多维随机变量及其分布函 掌握多维随机变量的联合分布,边缘 分布定义及计算,掌握二维离散及连 4.2二维离散型随机变 4 10 4.3二维连续型随机变量 续型随机变量的定义,掌握随机变量 独立性的定义及判断方法,熟练掌握 4.4随机变量的独立性 维随机变量函数分布的计算 4.5二维随机变量函数的分布 第五意随机变量的数字特征 5.1数学期望 掌握随机变量数字特征的基本定义及 52方差 计算 了解数字特征在实际问题中的 了解协方差,相关系数的计算 5.3协方差和相关系数 含义 公式 5.4大数定律和中心极限定理 第六章数理统计的基本概念 6.1总体与样本 学习数理统计的基本概念,掌握三个 6 62直方图与经验分布函数 常用分布的定义及相关定理,了解直 6 方图与经验分布函数的构造及应用 63二个常田分布 64统计量及抽样分布 掌握常用统计量的定义及分布 第七章参数估计 学习参数估计的基本思路和方法,熟 7 7.1点估计 练掌握点估计及单个正态总体参数的 6 7.2区间估计 置信区间估计的计算方法 第八章假设检验 理解假设检验的基本原理及方法。堂 8 8.1假设检验的基本概念 握单个正态总体参数检验的思路方法 4 82单个正态总体参数的检验 及解题思路 总计 64 五、说明 本课程与其他课程的关系 本课程所涉及的先修课程为数学分析和高等代数 后续课程:随机过程,方差分析,数学建模 本课程在教学内容上须有数学分析中的集合论,定积分,级数,二重积分的知识及高等代 数中的矩阵及其运算的知识为基础,所以本课程应在数学分析及高等代数课程结课之后安排, 20
20 理论部分 序号 教学内容提要 基本要求 学时 2.6 泊松逼近 3 第三章 随机变量及其分布 3.1 随机变量的概念 3.2 离散型随机变量 3.3 随机变量的分布函数 3.4 连续型随机变量 3.5 随机变量函数的分布 掌握随机变量及几个常用的离散型随 机变量的定义及相关计算,掌握分布 函数、连续型随机变量的定义,掌握 三种常用连续型随机变量的定义及相 关计算,熟练掌握随机变量函数分布 的计算 10 4 第四章 多维随机变量及其分布 4.1 多维随机变量及其分布函数 4.2 二维离散型随机变量 4.3 二维连续型随机变量 4.4 随机变量的独立性 4.5 二维随机变量函数的分布 掌握多维随机变量的联合分布,边缘 分布定义及计算,掌握二维离散及连 续型随机变量的定义, 掌握随机变量 独立性的定义及判断方法,熟练掌握 二维随机变量函数分布的计算 10 5 第五章 随机变量的数字特征 5.1 数学期望 5.2 方差 5.3 协方差和相关系数 5.4 大数定律和中心极限定理 掌握随机变量数字特征的基本定义及 计算,了解数字特征在实际问题中的 含义,了解协方差,相关系数的计算 公式 10 6 第六章 数理统计的基本概念 6.1 总体与样本 6.2 直方图与经验分布函数 6.3 三个常用分布 6.4 统计量及抽样分布 学习数理统计的基本概念,掌握三个 常用分布的定义及相关定理,了解直 方图与经验分布函数的构造及应用, 掌握常用统计量的定义及分布 6 7 第七章 参数估计 7.1 点估计 7.2 区间估计 学习参数估计的基本思路和方法,熟 练掌握点估计及单个正态总体参数的 置信区间估计的计算方法 6 8 第八章 假设检验 8.1 假设检验的基本概念 8.2 单个正态总体参数的检验 理解假设检验的基本原理及方法,掌 握单个正态总体参数检验的思路方法 及解题思路 4 总计 64 五、说明 本课程与其他课程的关系: 本课程所涉及的先修课程为:数学分析和高等代数 后续课程:随机过程,方差分析,数学建模 本课程在教学内容上须有数学分析中的集合论,定积分,级数,二重积分的知识及高等代 数中的矩阵及其运算的知识为基础,所以本课程应在数学分析及高等代数课程结课之后安排