
knowledge in limit theory,unary function,infinite series and multi-function is helpful for the students to foster dialectical materialism view,let them understand the basic concepts of mathematical analysis,master the demonstration method in mathematical analysis. acquire skill and preliminary application capacity. 《高等代数与解析几何(1)2)》 课程编号 0BL09907-8 学分 11 总学时 176 实验/上机学时 实验:0学时,上机:0学时 课程名称 高等代数与解析几何 英文名称 Advanced Algebra and Analytic (1)(2) Geometry (1)(2) 课程类别 必修 适用专业 信息与计算科学,应用统计学 执笔人 谢冬秀 审核人 王爱文 先修课程 初等数学 一、课程的地位与作用 本课程是数学各专业的主干基础课,它是数学在其它学科之应用的必需基础课程,又 是数学修养的核心课程,它的基本思想和基本方法将贯穿在所有的后续课程中。学好本课程 是完成本专业学习的必备条件之一。 二、课程对应的毕业要求 通过该课程的学习得到良好的数学训练,并具有扎实的数学基础和严密的逻辑思维能力, 通过该课程学习,针对复杂工程问颗。能铭理解和平价工程实际对白然环境、社会环培以及 可持续发展的影响。培养具有自主学习和终身学习的意识,有不断学习和适应发展的能力。 三、课程教学目标 培养具有扎实的数学基础和严密的逻辑思维能力:为今后运用代数、几何的思想、方法 解决更一般、更广泛的数学问题打下扎实的基础。掌握信息科学和计算科学的必备的数学基 本理论、方法与技能,受到科学研究的初步训练。 四、课程教学内容提要与基本要求 理论部分 序号 教学内容提要 基本要求 学时 解析几何部分 第一查向量代数 1.1向量及其表示 熟练掌握向量的线性关系,向量 的内积、外积和混合积,掌握二重外 10 12向量的线性运算 1.3向量的内积、外积与混合积 积的计算及相关理论
6 knowledge in limit theory, unary function calculus, infinite series and multi-function calculus. It is helpful for the students to foster dialectical materialism view, let them understand the basic concepts of mathematical analysis, master the demonstration method in mathematical analysis, acquire proficient calculation skill and preliminary application capacity. 《高等代数与解析几何(1)(2)》 课程编号 0BL09907-8 学 分 11 总 学 时 176 实验/上机学时 实验: 0 学时,上机: 0 学时 课程名称 高等代数与解析几何 (1)(2) 英文名称 Advanced Algebra and Analytic Geometry (1)(2) 课程类别 必修 适用专业 信息与计算科学,应用统计学 执 笔 人 谢冬秀 审 核 人 王爱文 先修课程 初等数学 一、课程的地位与作用 本课程是数学各专业的主干基础课,它是数学在其它学科之应用的必需基础课程,又 是数学修养的核心课程,它的基本思想和基本方法将贯穿在所有的后续课程中。学好本课程 是完成本专业学习的必备条件之一。 二、课程对应的毕业要求 通过该课程的学习得到良好的数学训练,并具有扎实的数学基础和严密的逻辑思维能力, 通过该课程学习,针对复杂工程问题,能够理解和评价工程实际对自然环境、社会环境以及 可持续发展的影响。培养具有自主学习和终身学习的意识,有不断学习和适应发展的能力。 三、课程教学目标 培养具有扎实的数学基础和严密的逻辑思维能力;为今后运用代数、几何的思想、方法 解决更一般、更广泛的数学问题打下扎实的基础。掌握信息科学和计算科学的必备的数学基 本理论、方法与技能,受到科学研究的初步训练。 四、课程教学内容提要与基本要求 理论部分 序号 教学内容提要 基本要求 学时 解析几何部分 1 第一章 向量代数 1.1 向量及其表示 1.2 向量的线性运算 1.3 向量的内积、外积与混合积 熟练掌握向量的线性关系,向量 的内积、外积和混合积,掌握二重外 积的计算及相关理论 10
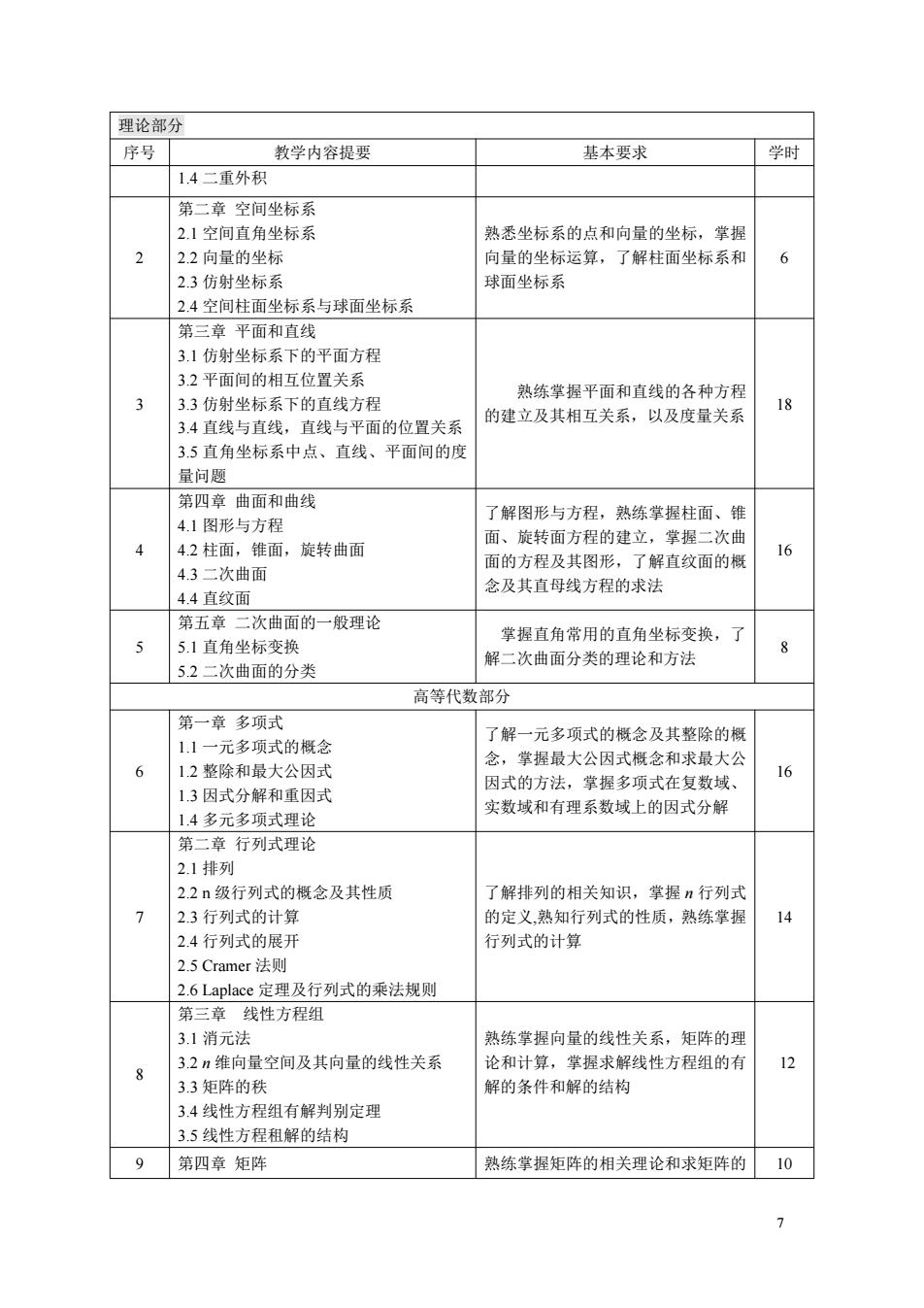
理论部分 序号 教学内容提要 基本要求 学时 1.4二重外积 第二章空间坐标系 2.1空间直角坐标系 熟悉坐标系的点和向量的坐标,掌拆 2 22向量的华标 向量的坐标运算,了解柱面坐标系和 6 23仿射坐标系 球面坐标系 2.4空间柱面坐标系与球面坐标系 第三章平面和直线 3.1仿射坐标系下的平面方程 32平面间的相五位曾关系 熟练掌握平面和直线的各种方程 33仿射坐标系下的直线方程 34直线与直线,直线与平面的位置关系 的建立及其相互关系,以及度量关系 3.5直角坐标系中点 直线、 平面间的房 量问题 第四章曲面和曲线 4.1图形与方程 了解图形与方程,熟练掌握柱面、锥 面、恢转面方程的建立,堂挥一次曲 4.2柱面,锥面,旋转曲面 面的方程及其图形 了解直纹面的概 16 4.3 次曲面 4.4直纹面 仑及其直母线方程的求法 第五章二次曲面的一般理论 掌握直角常用的直角坐标变换, 5.1直角坐标变换 52二次曲面的分类 解二次曲面分类的理论和方法 高等代数部分 第一章名项式 了解一元多项式的概会及其整除的根 1.1一元多项式的概今 今,堂探最大公因式概念和求最大乃 6 1)整险和最大公因式 因式的方法,掌握多项式在复数域、 16 1,3因式分解和重因式 实数域和有理系数域上的因式分解 1.4多元多项式理论 第二章行列式理论 21排列 22级行列式的概今及其性丽 了解排列的相关知识,堂据n行列式 2.3行列式的 的定义,熟知行列式的性质,熟练掌握 14 2.4行列式的展于 行列式的计算 2.5 Cramer法则 2.6 Laplace定理及行列式的乘法规则 第三章线性方程组 3.1消元法 熟练掌握向量的线性关系,矩阵的理 32n维向量空间及其向量的线性关系 论和计算 解线性方程组的有 12 33矩阵的秩 解的条件和解的结构 3.4线性方程组有解判别定理 3.5线性方程租解的结构 9 第四章矩阵 熟练掌握矩阵的相关理论和求矩阵的10 7
7 理论部分 序号 教学内容提要 基本要求 学时 1.4 二重外积 2 第二章 空间坐标系 2.1 空间直角坐标系 2.2 向量的坐标 2.3 仿射坐标系 2.4 空间柱面坐标系与球面坐标系 熟悉坐标系的点和向量的坐标,掌握 向量的坐标运算,了解柱面坐标系和 球面坐标系 6 3 第三章 平面和直线 3.1 仿射坐标系下的平面方程 3.2 平面间的相互位置关系 3.3 仿射坐标系下的直线方程 3.4 直线与直线,直线与平面的位置关系 3.5 直角坐标系中点、直线、平面间的度 量问题 熟练掌握平面和直线的各种方程 的建立及其相互关系,以及度量关系 18 4 第四章 曲面和曲线 4.1 图形与方程 4.2 柱面,锥面,旋转曲面 4.3 二次曲面 4.4 直纹面 了解图形与方程,熟练掌握柱面、锥 面、旋转面方程的建立,掌握二次曲 面的方程及其图形,了解直纹面的概 念及其直母线方程的求法 16 5 第五章 二次曲面的一般理论 5.1 直角坐标变换 5.2 二次曲面的分类 掌握直角常用的直角坐标变换,了 解二次曲面分类的理论和方法 8 高等代数部分 6 第一章 多项式 1.1 一元多项式的概念 1.2 整除和最大公因式 1.3 因式分解和重因式 1.4 多元多项式理论 了解一元多项式的概念及其整除的概 念,掌握最大公因式概念和求最大公 因式的方法,掌握多项式在复数域、 实数域和有理系数域上的因式分解 16 7 第二章 行列式理论 2.1 排列 2.2 n 级行列式的概念及其性质 2.3 行列式的计算 2.4 行列式的展开 2.5 Cramer 法则 2.6 Laplace 定理及行列式的乘法规则 了解排列的相关知识,掌握 n 行列式 的定义,熟知行列式的性质,熟练掌握 行列式的计算 14 8 第三章 线性方程组 3.1 消元法 3.2 n 维向量空间及其向量的线性关系 3.3 矩阵的秩 3.4 线性方程组有解判别定理 3.5 线性方程租解的结构 熟练掌握向量的线性关系,矩阵的理 论和计算,掌握求解线性方程组的有 解的条件和解的结构 12 9 第四章 矩阵 熟练掌握矩阵的相关理论和求矩阵的 10
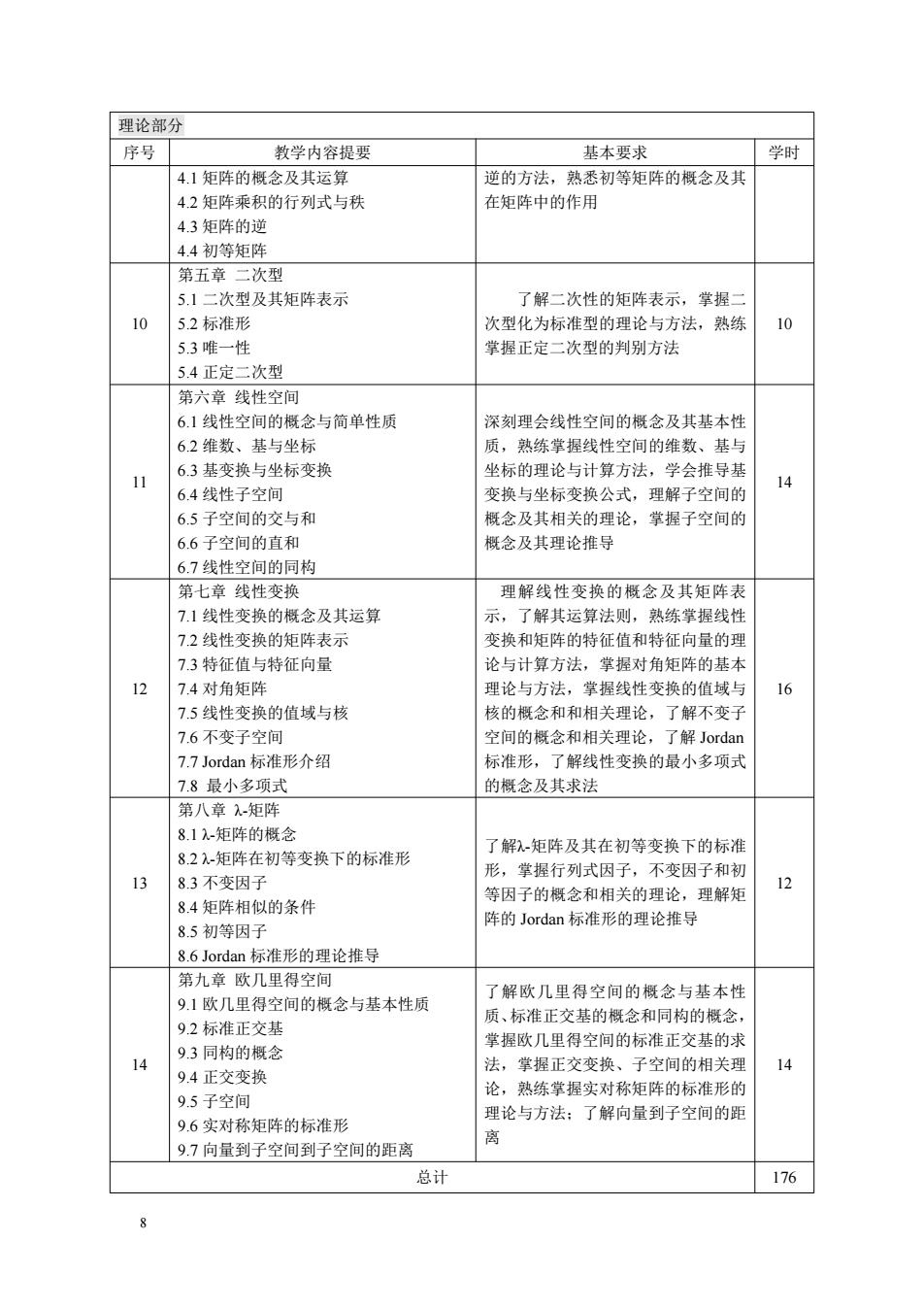
理论部分 序号 教学内容提要 基本要求 学时 41矩阵的概念及其坛算 逆的方法,熟悉初等矩阵的概念及其 42矩阵乘积的行列式与积 在矩阵中的作用 43面阵的道 4.4初等矩阵 第五章 二次至 5.1二次型及其矩阵表示 了解二次性的矩阵表示,掌握 10 52标准形 次型化为标准型的理论与方法,熟练 10 53惟一性 堂探正定一次型的判别方法 54正定 次 第六章线性空间 6.1线性空间的概念与简单性质 深刻理会线性空间的概今及其基本相 62维数、基与坐标 质,熟练掌握线性空间的维数、基与 63基变换与华标变 坐标的理论与计算方法,学会推导基 11 6.4线性 子空间 变换与坐标变换公式, 理解子空间的 14 6.5子空间的交与和 概念及其相关的理论, 草握子空间的 6.6子空间的直和 概念及其理论推导 6.7线性空间的同构 第七章线性变换 理解线性变换的概令及其矩阵表 7.1线性变换的概念及其运算 了解其运算法则,熟练掌握线性 7.2线性变换的矩阵表示 变换和矩阵的特征值和特征向量的理 73特征值与特征向量 论与计算方法,掌握对角矩阵的基本 12 74对角矩阵 理论与方法,掌据线性变换的值域上 6 75线性变换的值域与核 核的概念和和相关理论,了解不变子 7.6不变子空间 空间的据会和相关理论 了解Jordar Jordan标准形介绍 标准形 了解线性变换的最小多项 7.8最小多项式 的概念及其求法 第八章-矩阵 8.1-矩阵的概念 了解)矩阵及其在初等变换下的标准 8.2矩阵在初等变换下的标准形 不套因子和打 13 83不变因子 形,掌握行列式因子, 等因子的概念和相关的理论 理解 12 8.4矩阵相似的条件 8.5初等因子 阵的Jordan标准形的理论推导 8.6 lordan标准形的理论推导 第九意歌几里得空间 了解几里得空间的据与基木村 9.1欧几里得空间的概念与基本性质 9.2标准正交基 、标准正交基的概念和同构的概念 掌握欧几里得空间的标准正交基的求 9.3同构的概念 14 法,掌握正交变换、子空间的相关理 9.4正交变换 论,熟练掌握实对称矩阵的标准形的 95子空间 9.6实对称矩阵的标准形 理论与方法:了解向量到子空间的距 9,7向量到子空间到子空间的距离 离 总计 176
8 理论部分 序号 教学内容提要 基本要求 学时 4.1 矩阵的概念及其运算 4.2 矩阵乘积的行列式与秩 4.3 矩阵的逆 4.4 初等矩阵 逆的方法,熟悉初等矩阵的概念及其 在矩阵中的作用 10 第五章 二次型 5.1 二次型及其矩阵表示 5.2 标准形 5.3 唯一性 5.4 正定二次型 了解二次性的矩阵表示,掌握二 次型化为标准型的理论与方法,熟练 掌握正定二次型的判别方法 10 11 第六章 线性空间 6.1 线性空间的概念与简单性质 6.2 维数、基与坐标 6.3 基变换与坐标变换 6.4 线性子空间 6.5 子空间的交与和 6.6 子空间的直和 6.7 线性空间的同构 深刻理会线性空间的概念及其基本性 质,熟练掌握线性空间的维数、基与 坐标的理论与计算方法,学会推导基 变换与坐标变换公式,理解子空间的 概念及其相关的理论,掌握子空间的 概念及其理论推导 14 12 第七章 线性变换 7.1 线性变换的概念及其运算 7.2 线性变换的矩阵表示 7.3 特征值与特征向量 7.4 对角矩阵 7.5 线性变换的值域与核 7.6 不变子空间 7.7 Jordan 标准形介绍 7.8 最小多项式 理解线性变换的概念及其矩阵表 示,了解其运算法则,熟练掌握线性 变换和矩阵的特征值和特征向量的理 论与计算方法,掌握对角矩阵的基本 理论与方法,掌握线性变换的值域与 核的概念和和相关理论,了解不变子 空间的概念和相关理论,了解 Jordan 标准形,了解线性变换的最小多项式 的概念及其求法 16 13 第八章 λ-矩阵 8.1 λ-矩阵的概念 8.2 λ-矩阵在初等变换下的标准形 8.3 不变因子 8.4 矩阵相似的条件 8.5 初等因子 8.6 Jordan 标准形的理论推导 了解λ-矩阵及其在初等变换下的标准 形,掌握行列式因子,不变因子和初 等因子的概念和相关的理论,理解矩 阵的 Jordan 标准形的理论推导 12 14 第九章 欧几里得空间 9.1 欧几里得空间的概念与基本性质 9.2 标准正交基 9.3 同构的概念 9.4 正交变换 9.5 子空间 9.6 实对称矩阵的标准形 9.7 向量到子空间到子空间的距离 了解欧几里得空间的概念与基本性 质、标准正交基的概念和同构的概念, 掌握欧几里得空间的标准正交基的求 法,掌握正交变换、子空间的相关理 论,熟练掌握实对称矩阵的标准形的 理论与方法;了解向量到子空间的距 离 14 总计 176

五、说明 本课程在第1学年开设,是后续其它专业课的基础。本课程分两部分,其中解析几何 部分58学时,高等代数部分118学时。 六、学生成绩考核与评定方式 本课程考核方式为笔试、闭卷考试,成绩比例为:平时30%+期末70% 七、建议散材与参考书 使用教材:1.谢冬秀编著,解析几何,科学出版社,2009.1。 2.北京大学数学系编著,高等代数(第3版),高等教有出版社,2003 参考书:1.吕林根,徐子道编著,解析几何(第四版),高教教育出版社,2006。 2.吕林根编著,解析几何学习辅导书,高教教有出版社,2006。 3.陈志杰等编著,高等代数与解析几何习题精解,科学出版社,20022 4.丘维声编著,解析几何(第2版),北京大学出版社,1996。 5.丘维声,高等代数大学高等代数课程创新教材(上,下),清华大学出版社, 2010(6、10)。 6.孟道骥,高等代数与解析几何,科学出版社,2007.1。 八、课程中英文筒介 高等代数与解析几何是数学类本科生各专业的基础课,它既是学习近世代数、微分方程 数值计算方法等后续课程的必备知识,也是在自然科学和工程技术各领域中应用广泛的数学 工具。其主要任务是使学生获得数学的思想方法,掌握向量代数、平面与直线、曲面与曲线、 多项式理论、行列式理论、矩阵理论、线性方程组理论、空间理论、线性变换等方面的代数 与几何的系统知识 通过本课程的学习,使学生进一步掌握具体与抽象、特殊与一般、有限与无限等辩证关 系:逐步培养学生对真理知识的发现和创新的能力,训练其对特殊实例的观察、分析、归纳、 综合、抽象概括和探索性推理的能力。本课程的教学目的在于培养学生抽象思维、逻辑推理 能力以及解决实际问题能力 Advanced Algebra and Analytic Geometry is the mathematics undergraduates professional basic course.It is both necessary knowledge of the subsequent course of learning modern algebra, differential equations,numerical method and alsoa mathematical tool widely used in various fields of the natural sciences and engineering technology.Its main task is to enable students to obtain a mathematical way of thinking and to grasp theory knowledge of algebra and geometry system about the vector algebra,plane and straight lines,surfaces and curves, polynomial theory,the theory of determinants.matrix theory,the theory of linear equations.space theory.linear transformation et
9 五、说明 本课程在第 1 学年开设,是后续其它专业课的基础。本课程分两部分,其中解析几何 部分 58 学时,高等代数部分 118 学时。 六、学生成绩考核与评定方式 本课程考核方式为笔试、闭卷考试,成绩比例为:平时 30%+期末 70%。 七、建议教材与参考书 使用教材:1. 谢冬秀编著,解析几何,科学出版社,2009.1。 2. 北京大学数学系编著,高等代数(第 3 版),高等教育出版社,2003。 参考书:1. 吕林根,徐子道编著, 解析几何(第四版),高教教育出版社,2006。 2. 吕林根编著, 解析几何学习辅导书,高教教育出版社,2006。 3. 陈志杰等编著, 高等代数与解析几何习题精解,科学出版社, 2002.2。 4. 丘维声编著, 解析几何(第 2 版),北京大学出版社, 1996.。 5. 丘维声,高等代数-大学高等代数课程创新教材(上,下),清华大学出版社, 2010(6、10)。 6. 孟道骥,高等代数与解析几何,科学出版社,2007.1。 八、课程中英文简介 高等代数与解析几何是数学类本科生各专业的基础课,它既是学习近世代数、微分方程、 数值计算方法等后续课程的必备知识,也是在自然科学和工程技术各领域中应用广泛的数学 工具。其主要任务是使学生获得数学的思想方法,掌握向量代数、平面与直线、曲面与曲线、 多项式理论、行列式理论、矩阵理论、线性方程组理论、空间理论、线性变换等方面的代数 与几何的系统知识. 通过本课程的学习,使学生进一步掌握具体与抽象、特殊与一般、有限与无限等辩证关 系;逐步培养学生对真理知识的发现和创新的能力,训练其对特殊实例的观察、分析、归纳、 综合、抽象概括和探索性推理的能力。本课程的教学目的在于培养学生抽象思维、逻辑推理 能力以及解决实际问题能力。 Advanced Algebra and Analytic Geometry is the mathematics undergraduates professional basic course. It is both necessary knowledge of the subsequent course of learning modern algebra, differential equations, numerical calculation method and also a mathematical tool widely used in various fields of the natural sciences and engineering technology. Its main task is to enable students to obtain a mathematical way of thinking and to grasp theory knowledge of algebra and geometry system about the vector algebra, plane and straight lines, surfaces and curves, polynomial theory, the theory of determinants, matrix theory, the theory of linear equations, space theory, linear transformation etc
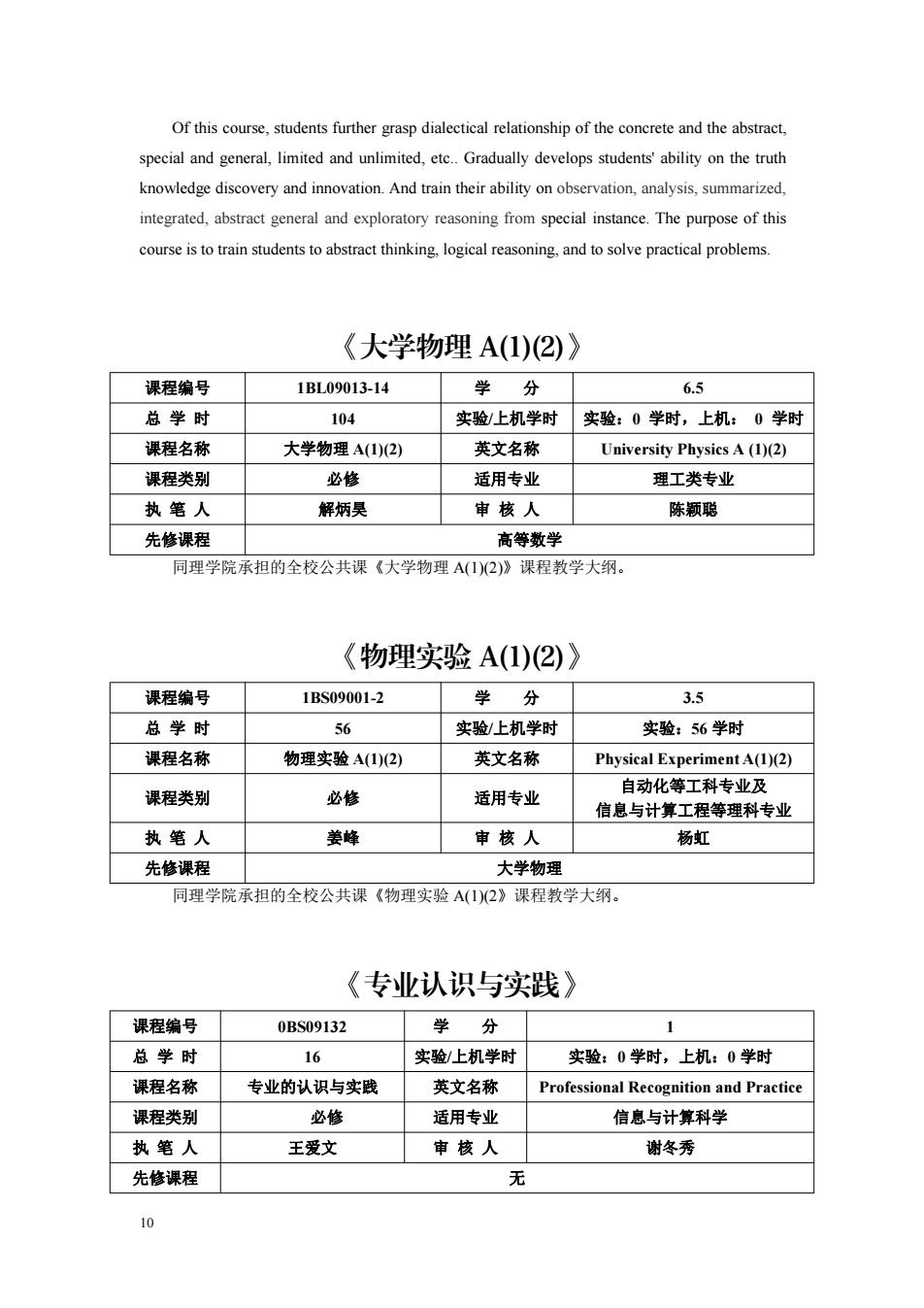
Of this course,students further grasp dialectical relationship of the conrete and the abstract. special and general,limited and unlimited,etc..Gradually develops students'ability on the truth knowledge discovery and innovation.And train their ability on observation.analysis.summarized integrated,abstract general and exploratory reasoning from special instance.The purpose of this ourse is to train students to abstract thinking logical reasoning and tosolve practical problems. 《大学物理A(1)2)》 课程编号 1BL09013-14 学分 6.5 总学时 实验/上机学时实验:0学时,上机:0学时 课程名称 大学物理A(1)(2) 英文名称 University Physics A(1)(2) 课程类别 必修 适用专业 理工类专业 执笔人 解炳吴 审核人 陈颖聪 先修课程 高等数学 同理学院承担的全校公共课《大学物理A(1)2)》课程教学大纲。 《物理实验A(1)②)》 课程编号 1BS09001-2 学分 3.5 总学时 56 实验/上机学时 实验:56学时 课程名称 物理实验A(1)(2) 英文名称 Physical ExperimentA(1)(2) 课程类别 必修 适用专业 自动化等工科专业及 信息与计算工程等理科专业 执笔人 姜峰 审核人 杨虹 先修课程 大学物理 同理学院承担的全校公共课《物理实验A(1(2》课程教学大纲。 《专业认识与实践》 课程编号 0BS09132 学分 总学时 16 实验/上机学时 实验:0学时,上机:0学时 课程名称 专业的认识与实践 英文名称 Professional Recognition and Practice 课程类别 必修 适用专业 信息与计算科学 执笔人 王爱文 审核人 谢冬秀 先修课程 无
10 Of this course, students further grasp dialectical relationship of the concrete and the abstract, special and general, limited and unlimited, etc.. Gradually develops students' ability on the truth knowledge discovery and innovation. And train their ability on observation, analysis, summarized, integrated, abstract general and exploratory reasoning from special instance. The purpose of this course is to train students to abstract thinking, logical reasoning, and to solve practical problems. 《大学物理 A(1)(2)》 课程编号 1BL09013-14 学 分 6.5 总 学 时 104 实验/上机学时 实验:0 学时,上机: 0 学时 课程名称 大学物理 A(1)(2) 英文名称 University Physics A (1)(2) 课程类别 必修 适用专业 理工类专业 执 笔 人 解炳昊 审 核 人 陈颖聪 先修课程 高等数学 同理学院承担的全校公共课《大学物理 A(1)(2)》课程教学大纲。 《物理实验 A(1)(2)》 课程编号 1BS09001-2 学 分 3.5 总 学 时 56 实验/上机学时 实验:56 学时 课程名称 物理实验 A(1)(2) 英文名称 Physical Experiment A(1)(2) 课程类别 必修 适用专业 自动化等工科专业及 信息与计算工程等理科专业 执 笔 人 姜峰 审 核 人 杨虹 先修课程 大学物理 同理学院承担的全校公共课《物理实验 A(1)(2》课程教学大纲。 《专业认识与实践》 课程编号 0BS09132 学 分 1 总 学 时 16 实验/上机学时 实验:0 学时,上机:0 学时 课程名称 专业的认识与实践 英文名称 Professional Recognition and Practice 课程类别 必修 适用专业 信息与计算科学 执 笔 人 王爱文 审 核 人 谢冬秀 先修课程 无