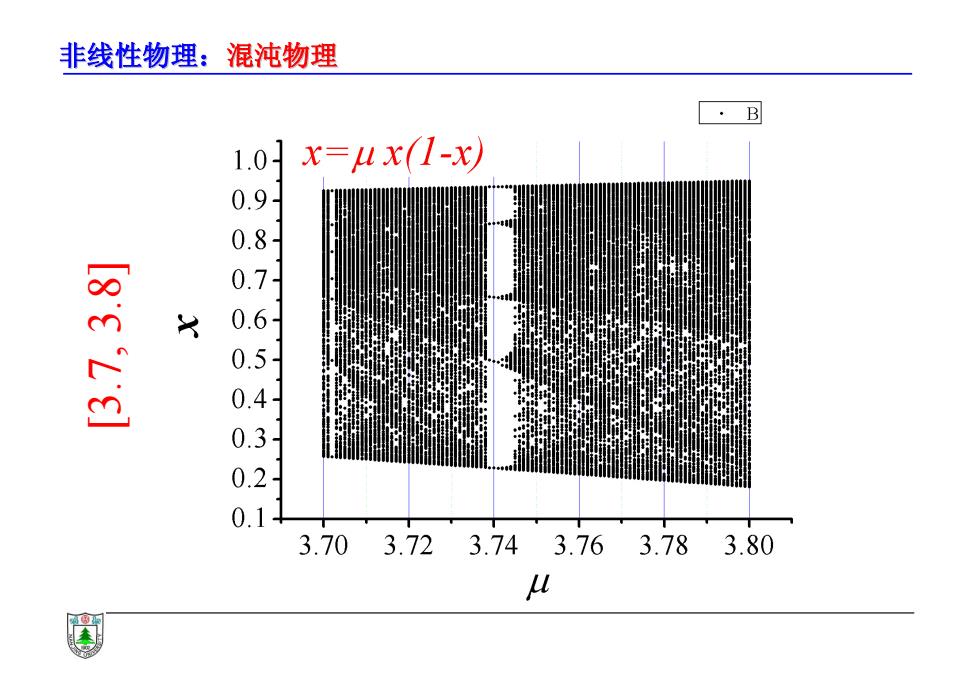
非线性物理:混沌物理 ·B 1.0 x=ux(1-x) 0.9 0.8 15.t.7tl 3.703.723.743.763.783.80 U
非线性物理:混沌物理 [3.7, 3.8]
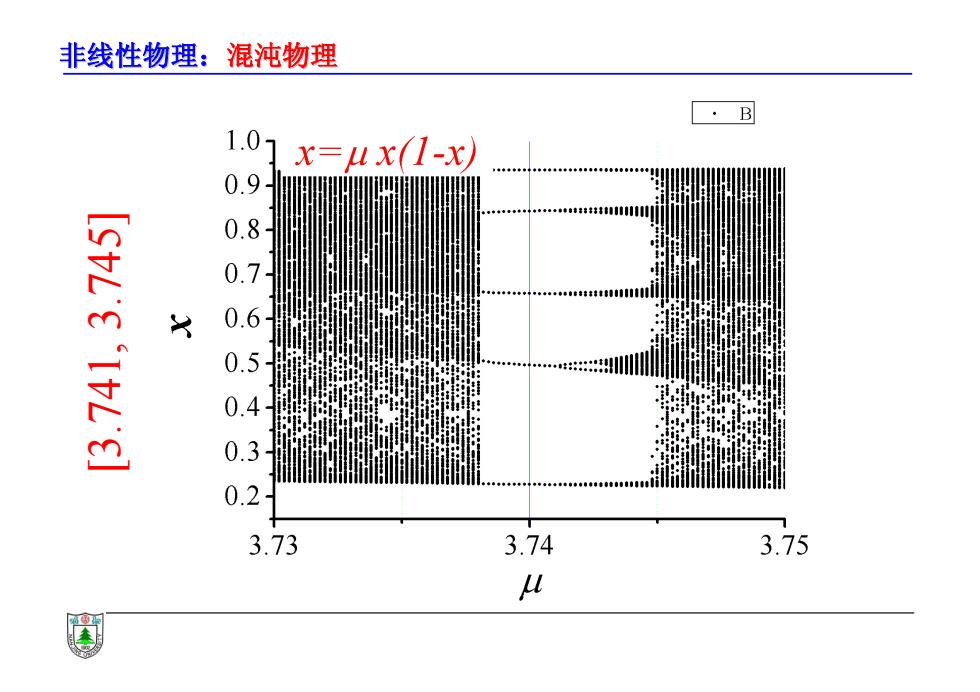
非线性物理:混沌物理 ·B 1.0 x=ux(1-x) 0.9 3.73 3.74 3.75 U
非线性物理:混沌物理 [3.741, 3.745]
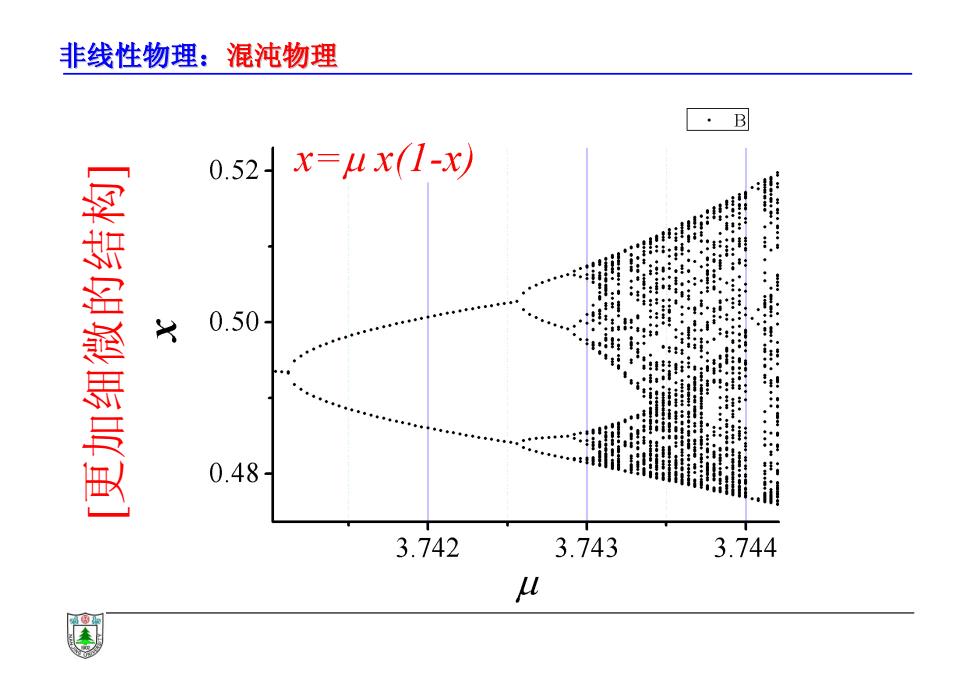
非线性物理:混沌物理 ·B 0.52x=4x(1-x 腓 0.50 。 0.48 3.742 3.743 3.744 u
非线性物理:混沌物理 [更加细微的结构]
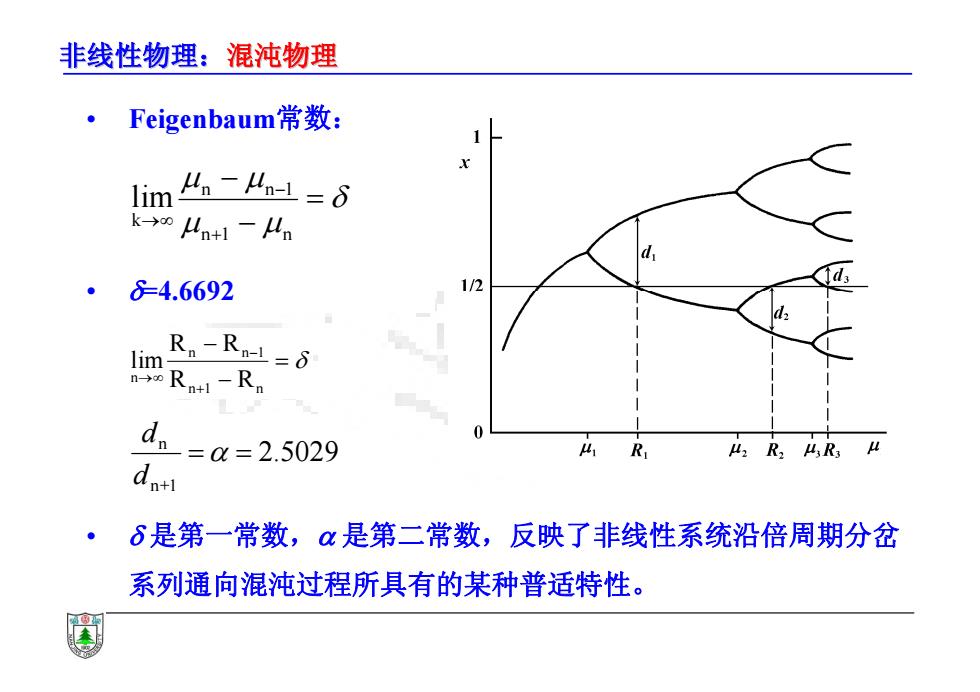
非线性物理:混沌物理 Feigenbaum常数: lim4。-4a1=6 k→oln+l-ln 。 84.6692 1/2 Rn-Rn-L=8 n→oRn+l-Rn dn=a=2.5029 0 41 42R24R3L dn+l 。 6是第一常数,α是第二常数,反映了非线性系统沿倍周期分岔 系列通向混沌过程所具有的某种普适特性
非线性物理:混沌物理 • Feigenbaum常数: n 1 n n n 1 k lim • =4.6692 lim n n n n1 n R R R R 1 • 是第一常数, 是第二常数,反映了非线性系统沿倍周期分岔 系列通向混沌过程所具有的某种普适特性。 2.5029 n+1 n d d

非线性物理:混沌物理 两个费根鲍姆常数虽然是在平方映射的计算中获得的,然而对于 所有在0,1]区间内为一条单峰的光滑曲线的映射都可计算得同样 的常数,例如正弦曲线、圆与椭圆曲线等等。 在许多包含耗散的非线性系统中,只要发生倍周期分岔序列也会 得到同样的普适常数。 。 费根鲍姆常数所包含的意义待进一步去发掘,它并不终止于某一 位数,现在常见的第一常数位数为4.66920160910209909..,第二 常数位数为2.502907875095
非线性物理:混沌物理 • 两个费根鲍姆常数虽然是在平方映射的计算中获得的,然而对于 所有在[0,1]区间内为一条单峰的光滑曲线的映射都可计算得同样 的常数,例如正弦曲线、圆与椭圆曲线等等。 • 在许多包含耗散的非线性系统中,只要发生倍周期分岔序列也会 得到同样的普适常数。 • 费根鲍姆常数所包含的意义待进一步去发掘,它并不终止于某一 位数,现在常见的第一常数位数为4.66920160910209909…,第二 常数位数为2.502907875095…