弯曲应力(四)最大正应力:M......(5)OmaxW中性轴1W.L抗弯截面模量。Ymax0(M)d元DIPC(1-α)圆环—一-WD32Ymaxbh3BH?11回字框 -- W. =BH36YmaxB
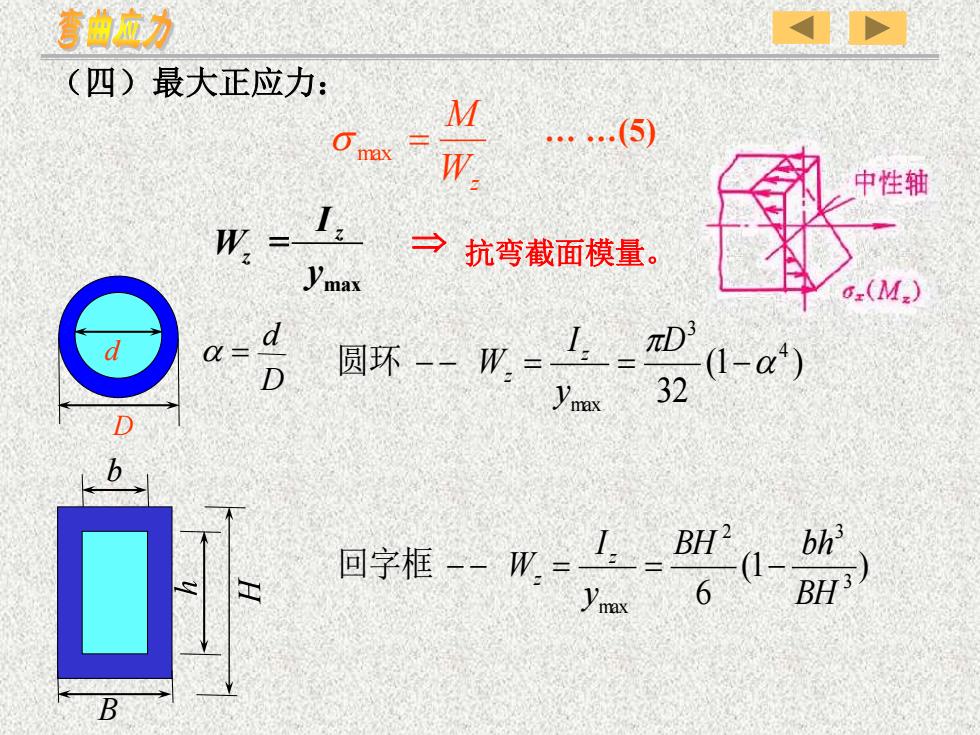
(四)最大正应力: Wz M s max = . .(5) D d D d a = (1 ) 32 4 3 max a − − = = − D y I W z 圆环 z b B (1 ) 6 3 2 3 max BH BH bh y I W z 回字框 − − z = = − max y I W z z = 抗弯截面模量
弯曲应力例1受均布载荷作用的简支梁如Q=60kN/m图所示,试求:B(1)11截面上1、2两点的正.A应力:2m1m(2)此截面上的最大正应力;13?(3)全梁的最大正应力;0812(4)己知E-200GPa,求1--1截120面的曲率半径。y解:①画M图求截面弯矩OqLM, =(qlx _ gx)M)- =60kNm福822MMmax
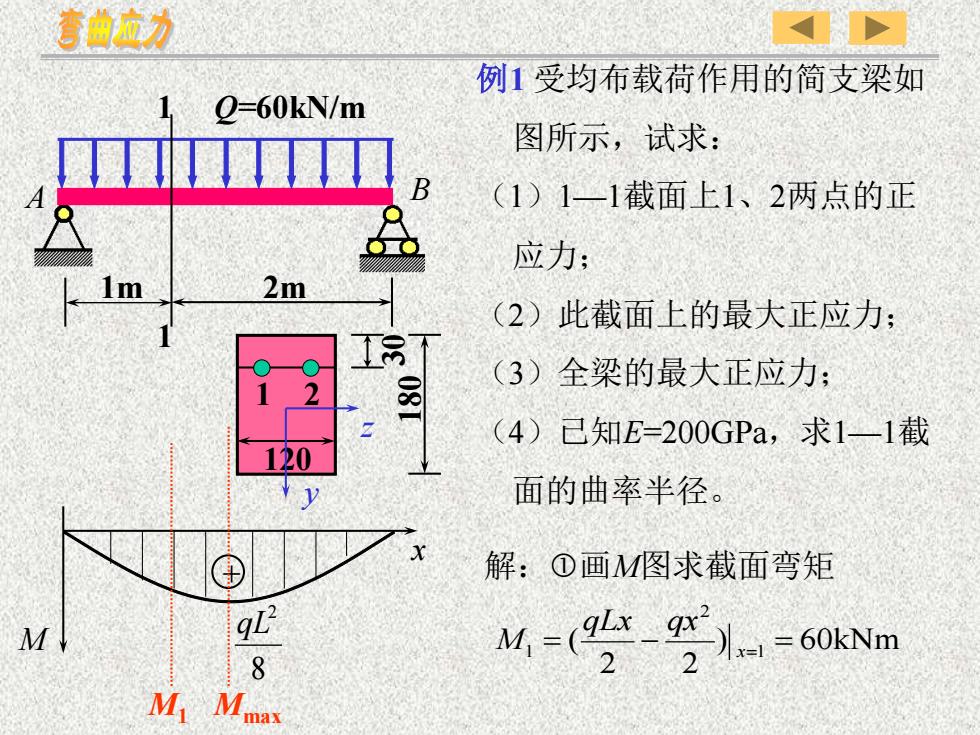
例1 受均布载荷作用的简支梁如 图所示,试求: (1)1—1截面上1、2两点的正 应力; (2)此截面上的最大正应力; (3)全梁的最大正应力; (4)已知E=200GPa,求1—1截 面的曲率半径。 Q=60kN/m A B 1m 2m 1 1 x M + 8 2 qL M1 Mmax 1 2 120 180 z y 解:画M图求截面弯矩 ) 60kNm 2 2 ( 1 2 1 = − x= = qLx qx M 30

弯曲应力M = qL/8= 60×32 /8= 67.5kNmQ=60kN/mB②求应力A.Rbh?120 ×18032m×10-12 = 5.832 ×10~ m4I.1m?121213工9福W = I /2=6.48×10-m30812120M.y0.=0,y1.- 60 ×60X×10° = 61.7MPa5.832qM I8MMmax
Q=60kN/m A B 1m 2m 1 1 x M + 8 2 qL M1 Mmax 1 2 120 z y / 8 60 3 /8 67.5kNm 2 2 Mmax = qL = = 1 2 5 4 3 3 10 5.832 10 m 12 120 180 12 − − = = = bh I z 4 3 / 2 6.48 10 m − Wz = I z = 10 61.7MPa 5.832 60 60 5 1 1 2 = − = = = z I M y s s 求应力 180 30

弯曲应力Q-60kN/m60MR×104 = 92.6MPaOimxBW.6.48A.AM67.52mmmax×104 = 104.2MPaO maxW.6.4813O08112③求曲率半径120El.200x5.832x×10=194.4mOPI.60M.qtMI8M Mmax
10 92.6MPa 6.48 1 60 4 1max = = = Wz M s 10 194.4m 60 200 5.832 1 1 = = = M EIz 10 104.2MPa 6.48 max 67.5 4 max = = = Wz M s 求曲率半径 Q=60kN/m A B 1m 2m 1 1 x M + 8 2 qL M1 Mmax 1 2 120 180 30