查曲应力85一2平面弯曲时梁横截面上的正应力纯弯曲时梁横截面上的正应力纵向对称面中性轴中性层(一)变形几何规律:1.梁的纯弯曲实验Va横向线(ab、cd)变5d形后仍为直线,但有转动;纵向线变为曲线,月上缩MMa下伸:横向线与纵向线变形后仍正交
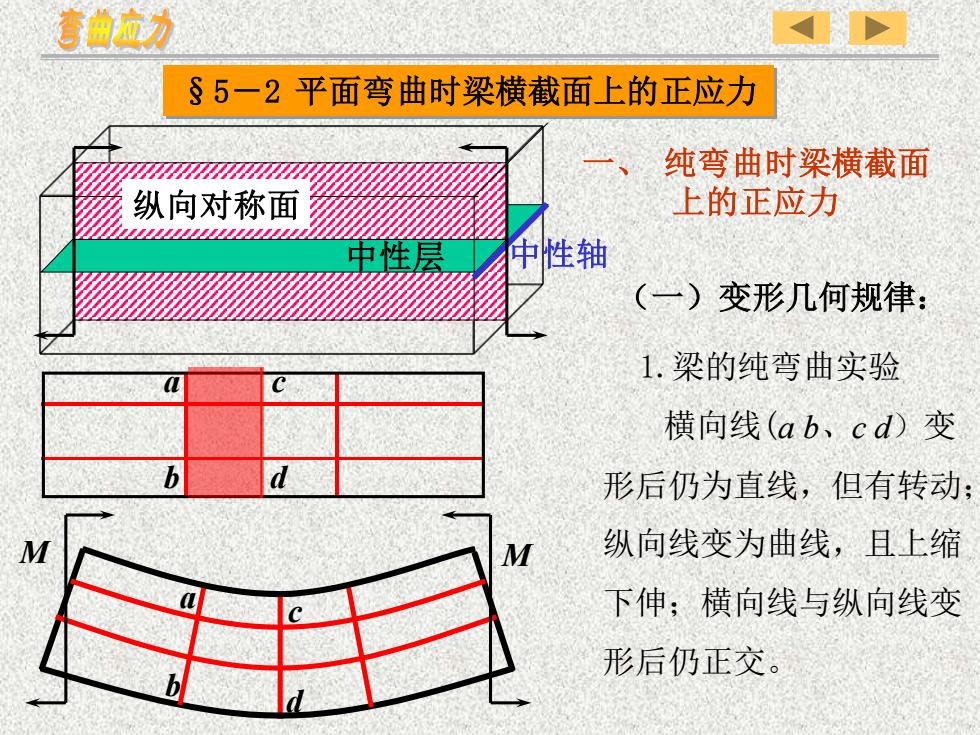
§5-2 平面弯曲时梁横截面上的正应力 1.梁的纯弯曲实验 横向线(a b、c d)变 形后仍为直线,但有转动; 纵向线变为曲线,且上缩 下伸;横向线与纵向线变 形后仍正交。 (一)变形几何规律: 一、 纯弯曲时梁横截面 上的正应力 中性层 纵向对称面 中性轴 b d a c a b c d M M

弯曲应力2.两个概念①中性层:梁内一层纤维既不伸长也不缩短,因而纤维不受拉应力和压应力,此层纤维称中性层。②中性轴:中性层与横截面的交线3. 推论①平面假设:横截面变形后仍为平面,只是绕中性轴发生转动距中性轴等高处,变形相等②横截面上只有正应力。(可由对称性及无限分割法证明福
横截面上只有正应力。 平面假设:横截面变形后仍为平面,只是绕中性轴发生转动, 距中性轴等高处,变形相等。 (可由对称性及无限分割法证明) 3.推论 2.两个概念 中性层:梁内一层纤维既不伸长也不缩短,因而纤维不 受拉应力和压应力,此层纤维称中性层。 中性轴:中性层与横截面的交线
查曲应力4.几何方程:AB -AB_4B -003deAB001ba(p+y)de-pdey0QBidA..A.B,Xcpdepyg=y(1)中性轴pC(M)
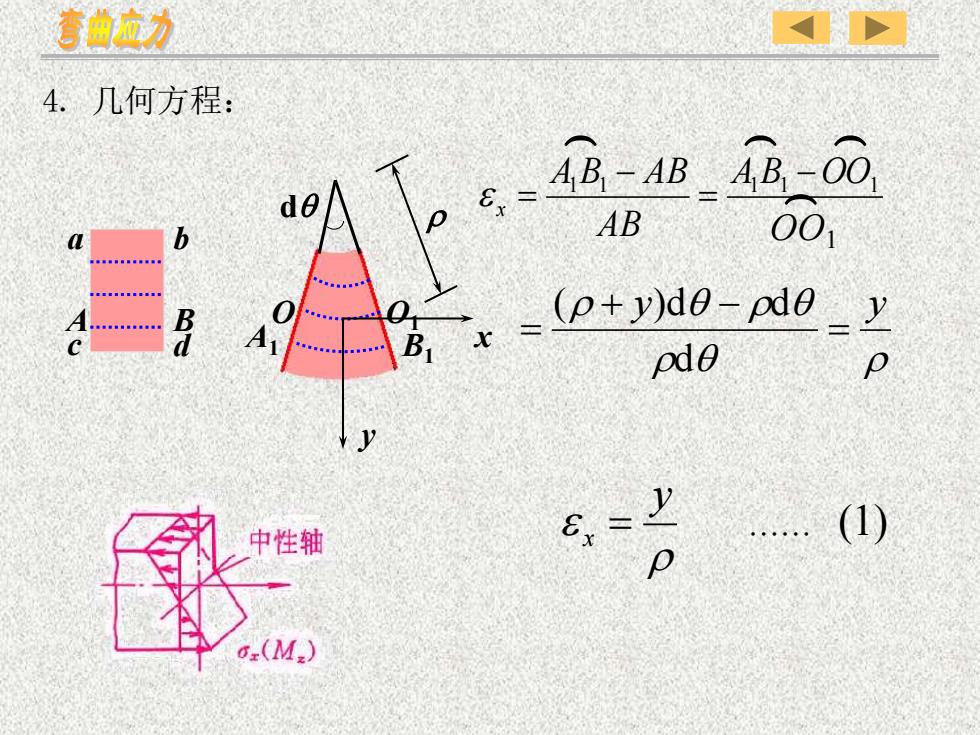
A1 B1 O O1 4. 几何方程: . (1) y x = a b c d A B dq x y 1 1 A1 B1 OO1 AB A B AB x − = − = ) ) ) OO1 ) q y q q y = + − = d ( )d d

弯曲应力(二)物理关系:假设:纵向纤维互不挤压。于是,任意一点均处于单项应力状态。OxOxEy(2)0,-Es.p(三)静力学关系:EN, - Jod4-IEYdA-EI yd4-ES.-0中性轴DS =O :.z (中性)轴过形心6+(M)
(二)物理关系: 假设:纵向纤维互不挤压。于是,任意一点均处于单项应 力状态。 .(2) s Ey x = E x = sx sx (三)静力学关系: = d = d = d = = 0 s z A A A x ES y A E A Ey N A Sz = 0 z(中性)轴过形心

弯曲应力ZM,-L(ad)--L E 4-L3d4-El-E0D(对称面)M,-L(od)y-E d4-E'd4-El -M1-M......(3)EI 一杆的抗弯刚度。EIpMy(4)中性轴I.0(M,)
= ( d ) = d = d = 0 s yz A A A y EI yz A E A Eyz M A z (对称面) M EI y A E A Ey M A y z A A A z = = = = = (sd ) d d 2 2 z z EI M = 1 . .(3) EIz 杆的抗弯刚度。 . (4) z x I M y s =