
第七章应力和应变分析强度理论 §7.1应力状态概述 §7.2二向和三向应力状态实例 §7.3二向应力状态分析一一解析法 §7.4二向应力状态分析一一图解法 §7.5三向应力状态 *§7.6位移与应变分量 *§7.7平面应变状态分析 §7.8广义胡克定律 §7.9复杂应力状态的应变能密度 §7.10强度理论概述 §7.11四种常用强度理论 §7.12莫尔强度理论 §7.1应力状态概述 E 1.应力状态的概念 m (1)一点的应力状态: 研究表明,构件内不同位置的点, 一般情况下具有不同的应力,所以点的 应力是该点坐标的函数。然而就一点来 论,不同方位截面上的应力也不同,截面上的应力又随截面方位的不
第七章 应力和应变分析 强度理论 §7.1 应力状态概述 §7.2 二向和三向应力状态实例 §7.3 二向应力状态分析——解析法 §7.4 二向应力状态分析——图解法 §7.5 三向应力状态 *§7.6 位移与应变分量 *§7.7 平面应变状态分析 §7.8 广义胡克定律 §7.9 复杂应力状态的应变能密度 §7.10 强度理论概述 §7.11 四种常用强度理论 §7.12 莫尔强度理论 §7.1 应力状态概述 1. 应力状态的概念 (1)一点的应力状态: 研究表明,构件内不同位置的点, 一般情况下具有不同的应力,所以点的 应力是该点坐标的函数。然而就一点来 论,不同方位截面上的应力也不同,截面上的应力又随截面方位的不
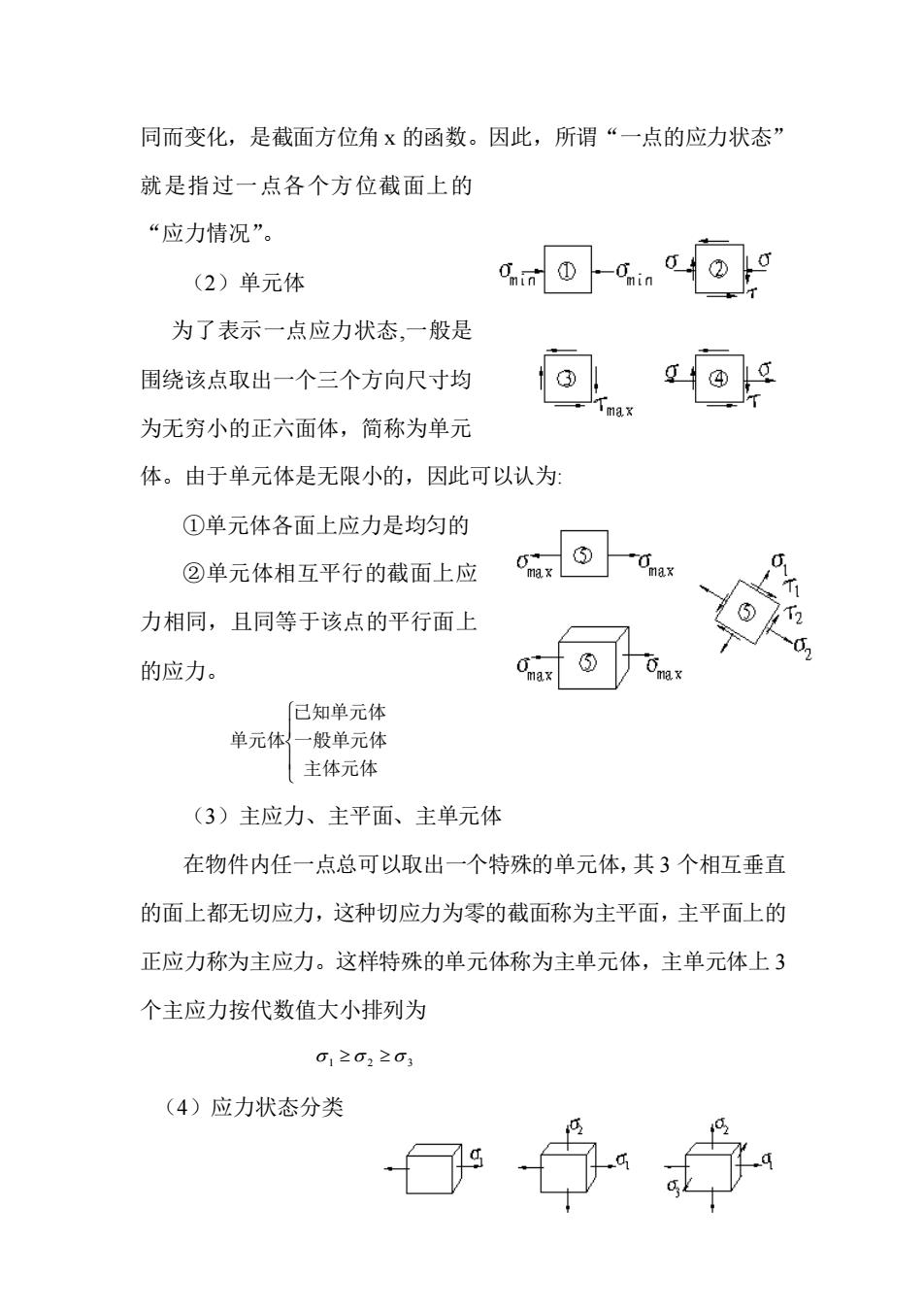
同而变化,是截面方位角x的函数。因此,所谓“一点的应力状态” 就是指过一点各个方位截面上的 “应力情况”。 (2)单元体 四-4②9 为了表示一点应力状态,一般是 围绕该点取出一个三个方向尺寸均 @4@9 为无穷小的正六面体,简称为单元 体。由于单元体是无限小的,因此可以认为 ①单元体各面上应力是均匀的 ②单元体相互平行的截面上应 力相同,且同等于该点的平行面上 的应力。 已知单元体 单元体{一般单元体 主体元体 (3)主应力、主平面、主单元体 在物件内任一点总可以取出一个特殊的单元体,其3个相互垂直 的面上都无切应力,这种切应力为零的截面称为主平面,主平面上的 正应力称为主应力。这样特殊的单元体称为主单元体,主单元体上3 个主应力按代数值大小排列为 01202203 (4)应力状态分类
同而变化,是截面方位角 x 的函数。因此,所谓“一点的应力状态” 就是指过一点各个方位截面上的 “应力情况”。 (2)单元体 为了表示一点应力状态,一般是 围绕该点取出一个三个方向尺寸均 为无穷小的正六面体,简称为单元 体。由于单元体是无限小的,因此可以认为: ①单元体各面上应力是均匀的 ②单元体相互平行的截面上应 力相同,且同等于该点的平行面上 的应力。 主体元体 一般单元体 已知单元体 单元体 (3)主应力、主平面、主单元体 在物件内任一点总可以取出一个特殊的单元体,其 3 个相互垂直 的面上都无切应力,这种切应力为零的截面称为主平面,主平面上的 正应力称为主应力。这样特殊的单元体称为主单元体,主单元体上 3 个主应力按代数值大小排列为 1 2 3 (4)应力状态分类
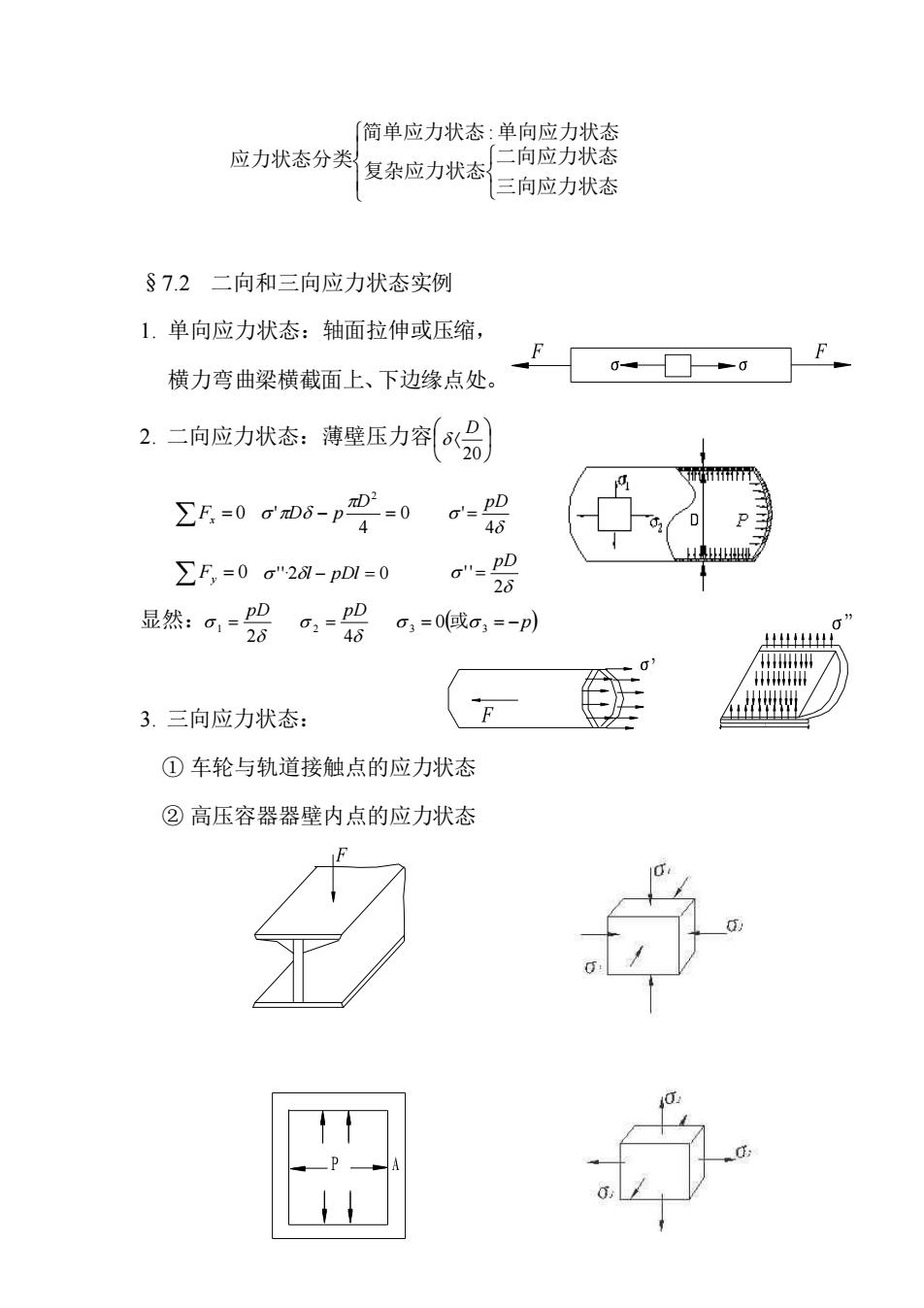
「简单应力状态:单向应力状态 应力状态分类复杂应力状态 二向应力状态 三向应力状态 §7.2二向和三向应力状态实例 1.单向应力状态:轴面拉伸或压缩, 横力弯曲梁横截面上、下边缘点处。 2二向应力状态:薄壁压力容(号)】 5-0g05-Y-0g岩 ∑F=0σ"2-pD1=0 。器 显然:a=岩=哈 0=0或o=-p) 3.三向应力状态: ①车轮与轨道接触点的应力状态 ②高压容器器壁内点的应力状态 P
三向应力状态 二向应力状态 复杂应力状态 简单应力状态 单向应力状态 应力状态分类 : §7.2 二向和三向应力状态实例 1. 单向应力状态:轴面拉伸或压缩, 横力弯曲梁横截面上、下边缘点处。 2. 二向应力状态:薄壁压力容 20 D Fx = 0 0 4 ' 2 − = D D p 4 ' pD = Fy = 0 ''·2l − pDl = 0 2 ' ' pD = 显然: 2 1 pD = 4 2 pD = = ( = −p) 3 0 或 3 3. 三向应力状态: ① 车轮与轨道接触点的应力状态 ② 高压容器器壁内点的应力状态

§73二向应力状态分析一一解析法 已知:O,tm,0,tx(应力符号规定:拉为正压 为负:切应力顺为正,逆为负),t,=t: 求:0,不,a符号逆时针为正 ①研究三棱柱单元的平衡 ∑F=0 d4+(dAcosa)sin a-(o,dAcosa)cosa -(sdAsin a)cosa-(,dAsin a)sin a=0 ∑F=0 rdA-(r dAcosa)cosa-(o,dAcosa)sin a -(,dAsin a)cosa+(dAsin a)sin a=0 dAcoso Ty=Tm 利用/cos'a=1+cos2g dAsinox m'a o2a 2smn acosa=sm 2a 简化后得出 =a,cosa+sin2a-2t sin acosa -+s2a-nm20 2 2 1,=0:,0m2a+t,os2a 2 ②求极值 0=-2sn2a+,s2a 12 (a) 若a=a,时,能使品-0,则a,所确定的截面上,正 应力即为最大值或最小值。以a,代入式(a),关令其 等于零,得到 g,-0sm2a,+r,0s2a=0 2
§7.3 二向应力状态分析——解析法 已知: x xu y yx , , , (应力符号规定:拉为正压 为负;切应力顺为正,逆为负), xy yx = 求: x , x ,符号逆时针为正 ①研究三棱柱单元的平衡 ( ) ( ) − ( ) − ( ) = + − = d sin cos d sin sin 0 d d cos sin d cos cos 0 A A A A A F yx y xy x n ( ) ( ) − ( ) + ( ) = − − = d sin cos d sin sin 0 d d cos cos d cos sin 0 A A A A A F y yx xy x z 利用 = − = + = = 2sin cos sin 2 2 1 cos 2 sin 2 1 cos 2 cos 2 2 xy yx 简化后得出 + − = − − + + = = + − sin 2 cos 2 2 cos 2 sin 2 2 2 cos sin 2 sin cos 2 2 xy x y xy x y x y x y xy ②求极值 + − = − sin 2 cos 2 2 2 d d xy x y (a) 若 = 0 时,能使 0 d d = ,则 0 所确定的截面上,正 应力即为最大值或最小值。以 0 代入式(a),关令其 等于零,得到 sin 2 cos 2 0 2 0 + 0 = − xy x y

由此得出:am2a,=0,-a 解之得:a,a。+90°确定相互垂直的两个平面,对应截面上出现正 应的极大值和极小值 注意到 ,sin 20+cs2do=ta-0 (b) 2 结论: 在切应力为零的平面上正应力极大值和极小值,即最大正应 力和最小正应力,就是主应力。所在的平面为主平面。 为了方便起见,利用三角恒等式 tan 20o=- 2t 0-0 0x-0, c0s2a0=± 1+tan 2aoV,-,+4 sin24=± 版 由讨论知cos2a,与sn2a,总取相反符号,代入式得: Ra.-att 2 讨论: 「若xn0,则o与过二,四相限的a,对应, 若rn0,则o与过一,三相限的a对应 ③最大切应力rm和最小切应力 dr=(-,)cos2a-2t sin 2a (c) da 若a=a时,能使品=0,则在a,所决定的斜截面上,切
由此得出: x y xy − = − 2 tan 2 0 解之得: 0 0 , 0 + 90 确定相互垂直的两个平面,对应截面上出现正 应的极大值和极小值。 注意到 sin 2 cos 2 0 2 0 + 0 = 0 = − xy x y (b) 结论: 在切应力为零的平面上正应力极大值和极小值,即最大正应 力和最小正应力,就是主应力。所在的平面为主平面。 为了方便起见,利用三角恒等式 ( ) ( ) 2 2 0 2 0 0 2 2 0 2 0 0 4 2 1 tan 2 tan 2 sin 2 1 tan 2 4 1 cos 2 2 tan 2 x y xy xy x y xy x y x y xy − + = + = − + − = + = − = − 由讨论知 2 0 cos 与 2 0 sin 总取相反符号,代入式得: 2 2 min max 2 2 xy x y x y + − + = 讨论: 0, , . 0, , , max 0 max 0 若 则 与过一 三相限的 对应 若 则 与过二 四相限的 对应 xy xy ③最大切应力 max 和最小切应力 ( ) cos 2 2 sin 2 d d = x − y − xy (c) 若 =1 时,能使 0 d d = ,则在 1 所决定的斜截面上,切