
第二章拉伸、压缩与剪切 §2.1轴向拉伸与压缩的概念和实例 §2.2轴向拉伸或压缩时横截面上的内力和应力 §2.3直杆轴向拉伸或压缩时斜截面上的应力 §2.4材料拉伸时的力学性能 §2.5材料压缩时的力学性能 §2.7失效、安全因数和强度计算 §2.8轴向拉伸或压缩时的变形 §2.9轴向拉伸或压缩的应变能 §2.10拉伸、压缩超静定问题 §2.11温度应力和装配应力 §2.12应力集中的概念 §2.13剪切和挤压的实用计算 §2.1轴向拉伸与压缩的概念和实例 1.实例 (1)液压传动中的活塞杆 (2)内燃机的连杆 (3)汽缸的联接螺栓 (4)起吊重物用的钢索 (5)千斤顶的螺杆 (6)桁架的杆件
第二章拉伸、压缩与剪切 §2.1 轴向拉伸与压缩的概念和实例 §2.2 轴向拉伸或压缩时横截面上的内力和应力 §2.3 直杆轴向拉伸或压缩时斜截面上的应力 §2.4 材料拉伸时的力学性能 §2.5 材料压缩时的力学性能 §2.7 失效、安全因数和强度计算 §2.8 轴向拉伸或压缩时的变形 §2.9 轴向拉伸或压缩的应变能 §2.10 拉伸、压缩超静定问题 §2.11 温度应力和装配应力 §2.12 应力集中的概念 §2.13 剪切和挤压的实用计算 §2.1 轴向拉伸与压缩的概念和实例 1.实例 (1)液压传动中的活塞杆 (2)内燃机的连杆 (3)汽缸的联接螺栓 (4)起吊重物用的钢索 (5)千斤顶的螺杆 (6)桁架的杆件
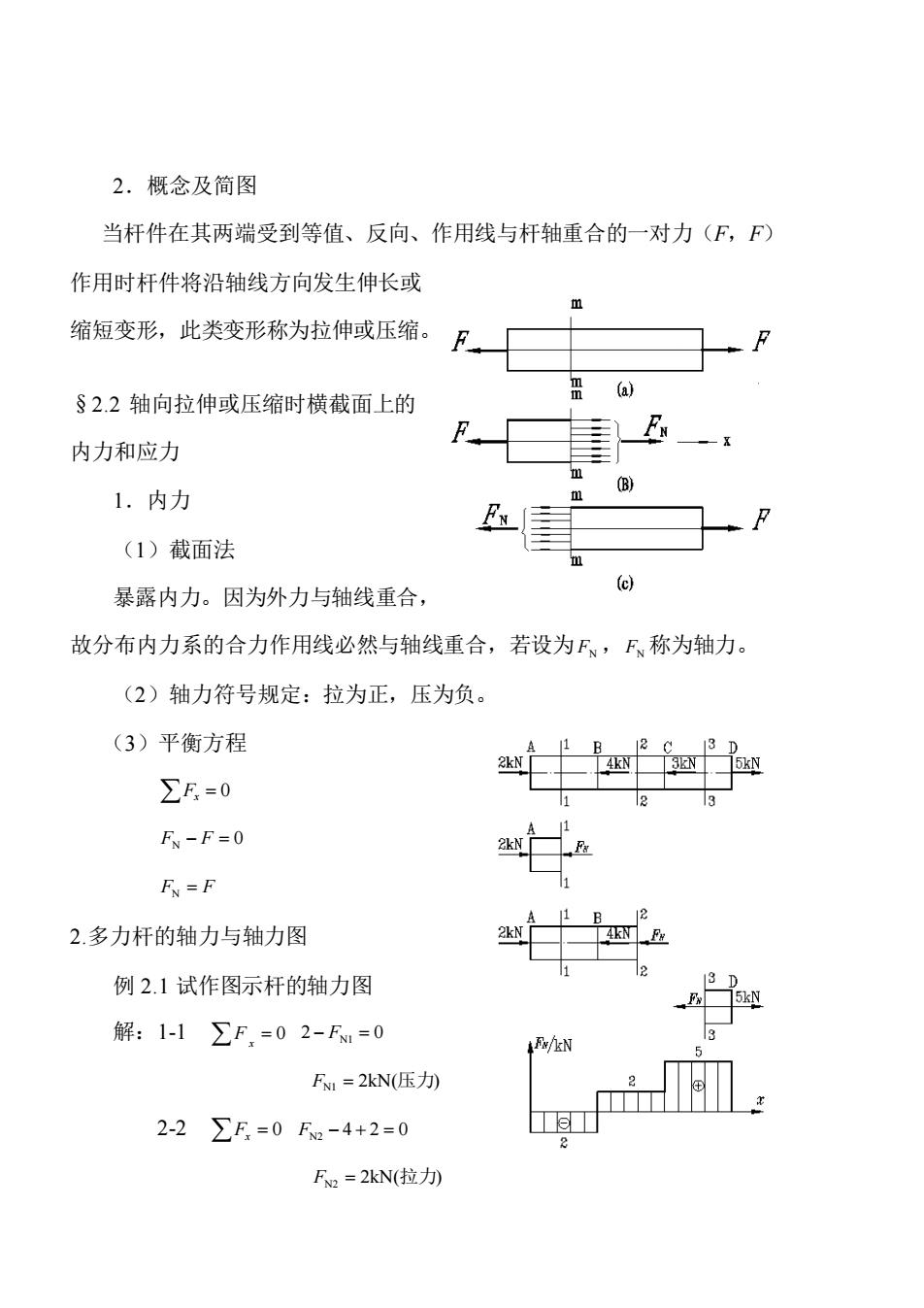
2.概念及简图 当杆件在其两端受到等值、反向、作用线与杆轴重合的一对力(F,F) 作用时杆件将沿轴线方向发生伸长或 缩短变形,此类变形称为拉伸或压缩。 (a) §2.2轴向拉伸或压缩时横截面上的 内力和应力 1.内力 (1)截面法 暴露内力。因为外力与轴线重合, 故分布内力系的合力作用线必然与轴线重合,若设为F,F称为轴力。 (2)轴力符号规定:拉为正,压为负。 (3)平衡方程 1 R 2013D ∑F=0 23 F-F=0 F=F 2.多力杆的轴力与轴力图 例2.1试作图示杆的轴力图 解:1-1∑F,=02-F=0 F1=2kN压) 2-2∑F=0Fa-4+2=0 F2=2kN(拉力
2.概念及简图 当杆件在其两端受到等值、反向、作用线与杆轴重合的一对力(F,F) 作用时杆件将沿轴线方向发生伸长或 缩短变形,此类变形称为拉伸或压缩。 §2.2 轴向拉伸或压缩时横截面上的 内力和应力 1.内力 (1)截面法 暴露内力。因为外力与轴线重合, 故分布内力系的合力作用线必然与轴线重合,若设为 FN ,FN 称为轴力。 (2)轴力符号规定:拉为正,压为负。 (3)平衡方程 Fx = 0 FN − F = 0 FN = F 2.多力杆的轴力与轴力图 例 2.1 试作图示杆的轴力图 解:1-1 = 0 x F 2 − FN1 = 0 2kN( ) FN1 = 压力 2-2 Fx = 0 FN2 − 4 + 2 = 0 2kN( ) FN2 = 拉力
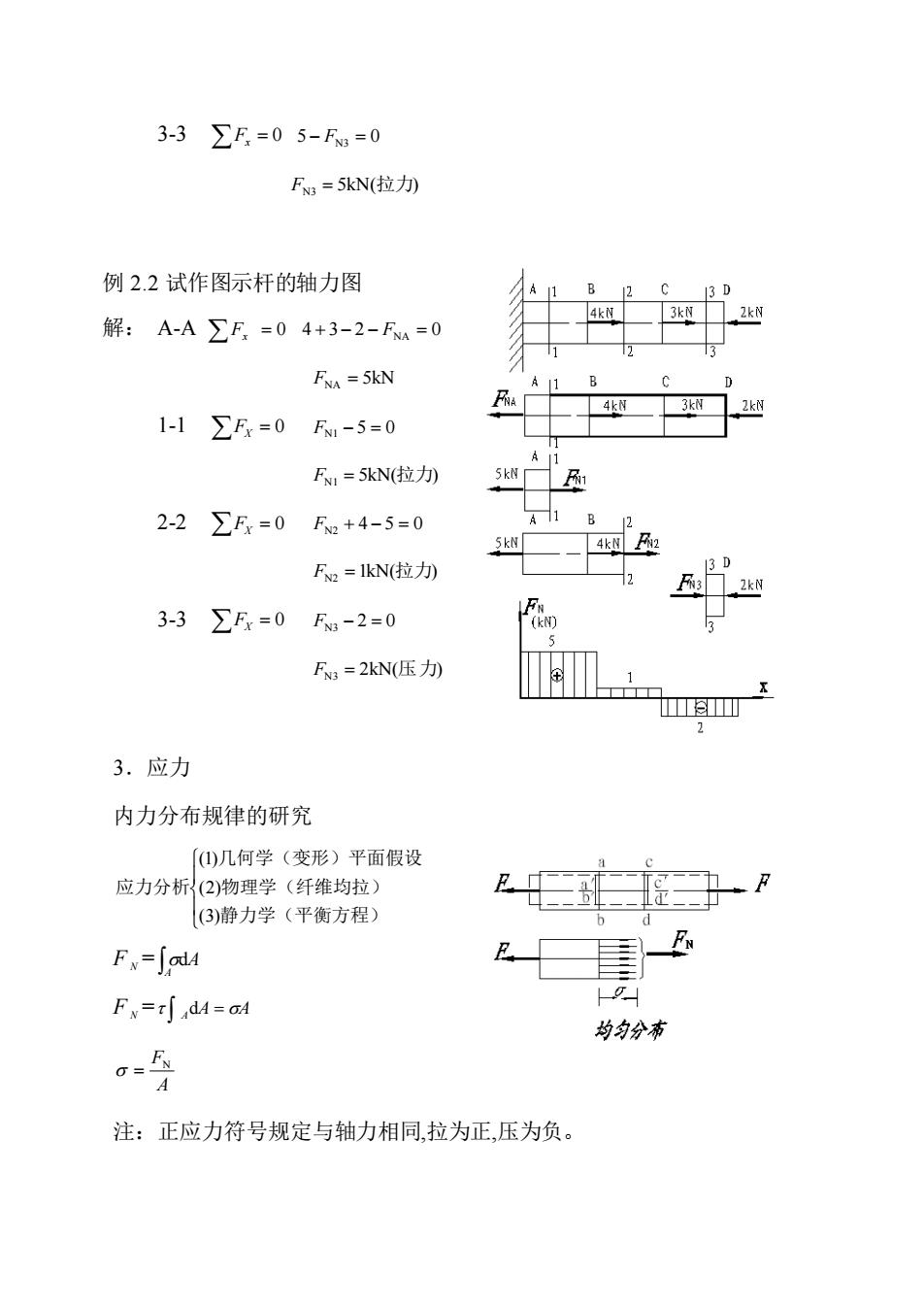
3-3∑F=05-R=0 F=5kN(拉 例2.2试作图示杆的轴力图 解:A-A∑F,=04+3-2-F=0 FNA 5kN RA 1-1∑Fx=0F1-5=0 FN,=5kN(拉) 5kNi 2-2∑Fx=0F2+4-5=0 B Fa=IkN(拉) 2kN 3-3∑F=0F-2=0 F=2N(压九 3.应力 内力分布规律的研究 [仙)几何学(变形)平面假设 应力分析(2)物理学(纤维均拉) (3)静力学(平衡方程) Fx-∫aM Fx=rdA=aA 均的分布 注:正应力符号规定与轴力相同,拉为正,压为负
3-3 Fx = 0 5 − FN3 = 0 5kN( ) FN3 = 拉力 例 2.2 试作图示杆的轴力图 解: A-A Fx = 0 4 + 3− 2 − FNA = 0 FNA = 5kN 1-1 FX = 0 FN1 − 5 = 0 5kN( ) FN1 = 拉力 2-2 FX = 0 FN2 + 4 − 5 = 0 1kN( ) FN2 = 拉力 3-3 FX = 0 FN3 − 2 = 0 2kN( ) FN3 = 压力 3.应力 内力分布规律的研究 静力学(平衡方程) 物理学(纤维均拉) 几何学(变形)平面假设 应力分析 (3) (2) (1) F N = A dA F N = A A = A d A F = 注:正应力符号规定与轴力相同,拉为正,压为负
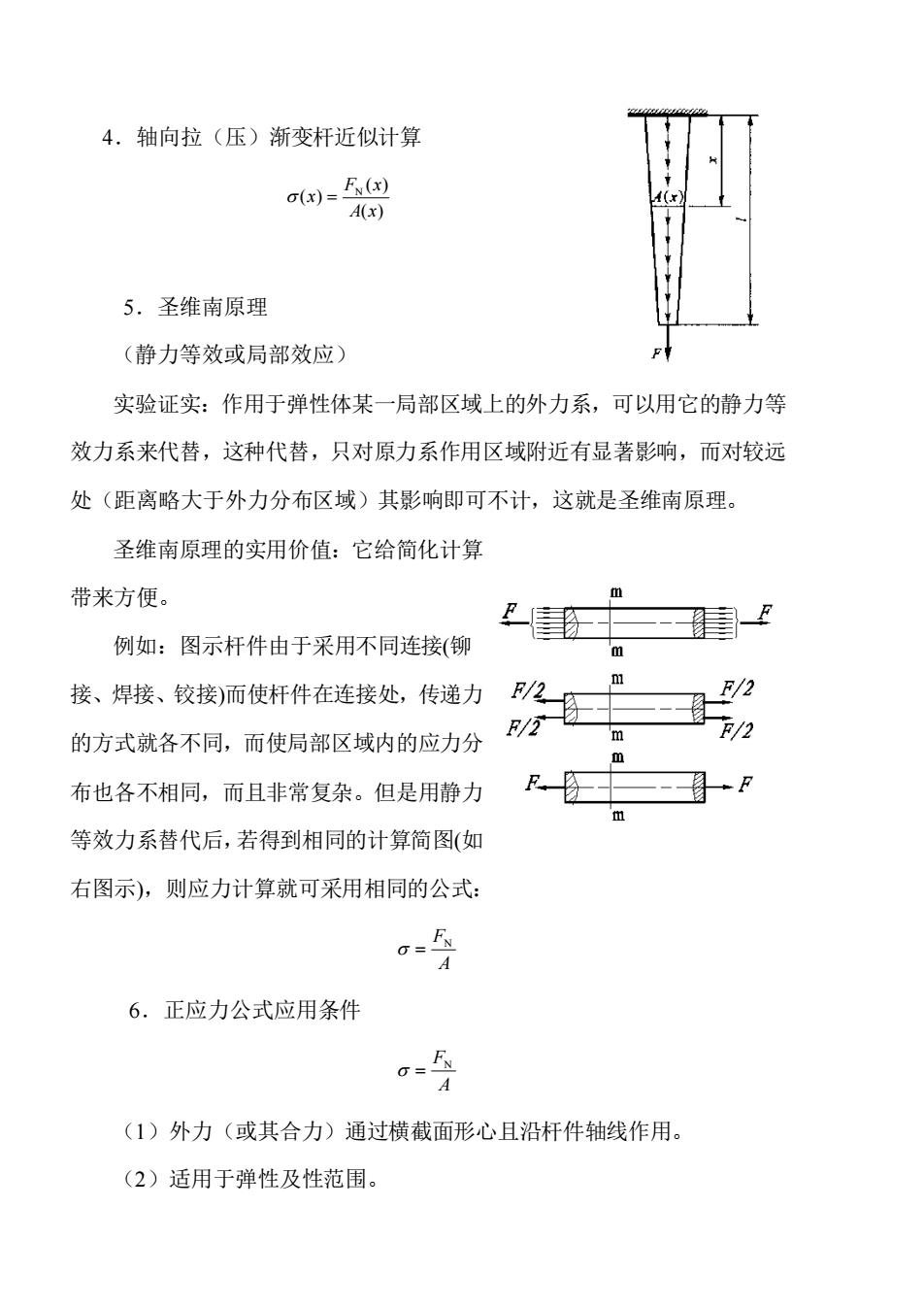
4.轴向拉(压)渐变杆近似计算 ()= A(x) 5.圣维南原理 (静力等效或局部效应) 实验证实:作用于弹性体某一局部区域上的外力系,可以用它的静力等 效力系来代替,这种代替,只对原力系作用区域附近有显著影响,而对较远 处(距离略大于外力分布区域)其影响即可不计,这就是圣维南原理。 圣维南原理的实用价值:它给简化计算 带来方便。 例如:图示杆件由于采用不同连接(铆 m F/2 m 接、焊接、铰接)而使杆件在连接处,传递力 F/2 F/2 的方式就各不同,而使局部区域内的应力分 m F/2 布也各不相同,而且非常复杂。但是用静力 等效力系替代后,若得到相同的计算简图(如 右图示),则应力计算就可采用相同的公式: A 6.正应力公式应用条件 = A (1)外力(或其合力)通过横截面形心且沿杆件轴线作用。 (2)适用于弹性及性范围
4.轴向拉(压)渐变杆近似计算 ( ) ( ) ( ) A x F x x = 5.圣维南原理 (静力等效或局部效应) 实验证实:作用于弹性体某一局部区域上的外力系,可以用它的静力等 效力系来代替,这种代替,只对原力系作用区域附近有显著影响,而对较远 处(距离略大于外力分布区域)其影响即可不计,这就是圣维南原理。 圣维南原理的实用价值:它给简化计算 带来方便。 例如:图示杆件由于采用不同连接(铆 接、焊接、铰接)而使杆件在连接处,传递力 的方式就各不同,而使局部区域内的应力分 布也各不相同,而且非常复杂。但是用静力 等效力系替代后,若得到相同的计算简图(如 右图示),则应力计算就可采用相同的公式: A F = 6.正应力公式应用条件 A F = (1)外力(或其合力)通过横截面形心且沿杆件轴线作用。 (2)适用于弹性及性范围
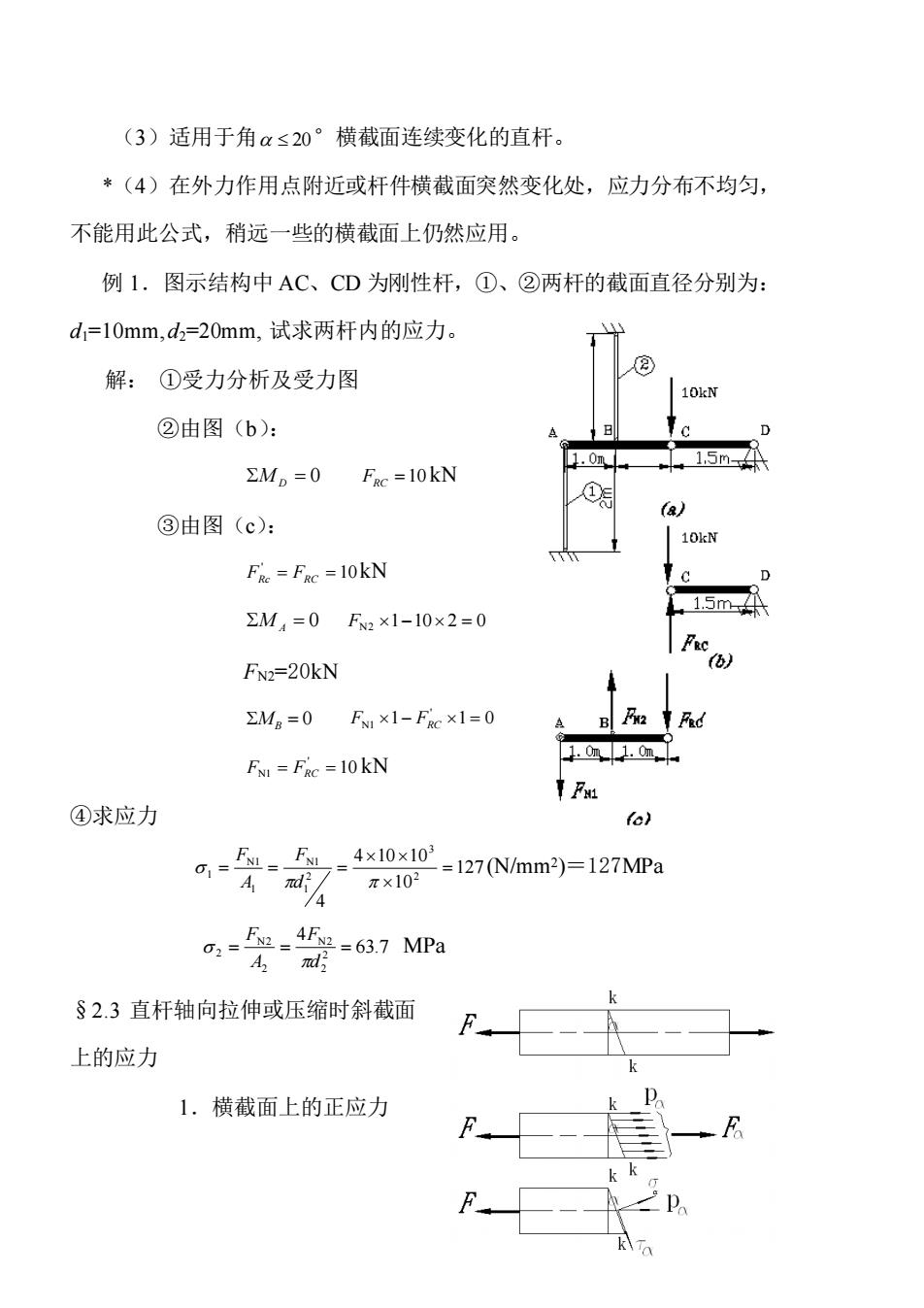
(3)适用于角α≤20°横截面连续变化的直杆。 *(4)在外力作用点附近或杆件横截面突然变化处,应力分布不均匀, 不能用此公式,稍远一些的横截面上仍然应用。 例1.图示结构中AC、CD为刚性杆,①、②两杆的截面直径分别为: d1=10mm,d2=20mm,试求两杆内的应力。 解:①受力分析及受力图 OkN ②由图(b): ΣMD=0Fac=I0kN 2.0+ 15m a ③由图(c): FRe Fgc =10kN 1.5m= EM4=0F2×1-10×2=0 FN2=20kN ∑Ma=0FN×1-Fc×1=0 FN FRc =10kN ④求应力 c 6,-型=7于40a-127Nmm29-127MPa π×102 §2.3直杆轴向拉伸或压缩时斜截面 F■ 上的应力 1.横截面上的正应力
(3)适用于角 20 °横截面连续变化的直杆。 *(4)在外力作用点附近或杆件横截面突然变化处,应力分布不均匀, 不能用此公式,稍远一些的横截面上仍然应用。 例 1.图示结构中 AC、CD 为刚性杆,①、②两杆的截面直径分别为: d1=10mm, d2=20mm, 试求两杆内的应力。 解: ①受力分析及受力图 ②由图(b): M D = 0 FRC =10 kN ③由图(c): 10 ' FRc = FRC = kN M A = 0 F2 1−10 2 = 0 FN2=20kN MB = 0 1 1 0 ' F1 − FRC = 10 ' F1 = FRC = kN ④求应力 127 10 4 10 10 4 2 3 2 1 1 1 1 1 = = = = d F A F (N/mm2 )=127MPa 63.7 4 2 2 2 2 2 2 = = = d F A F MPa §2.3 直杆轴向拉伸或压缩时斜截面 上的应力 1.横截面上的正应力