
第六章弯曲变形 §6.1工程中的弯曲变形问题 §6.2挠曲线的微分方程 §6.3用积分法求弯曲变形 §6.4用叠加法求弯曲变形 §6.5简单超静定梁 §6.6提高弯曲刚度的一些措施 §6.1工程中的弯曲变形问题 1.实例 ①车床主轴:变形过大,会使齿轮啮合不良,轴与轴承产生非均匀磨 损,产生噪声,降低寿命,影响加工精度。 ②吊车梁:变形过大会出现小车爬坡现象,引起振动。 2.研究变形目的 ①建立刚度条件,解决刚度问题 ②建立变形协调条件,解决超静定问题 ③为振动计算奠定基础。 §6.2挠曲线的微分方程 1.概念 以简支梁为例,以变形前的轴线为x轴,垂直向上为y轴,Oy平面
第六章 弯曲变形 §6.1 工程中的弯曲变形问题 §6.2 挠曲线的微分方程 §6.3 用积分法求弯曲变形 §6.4 用叠加法求弯曲变形 §6.5 简单超静定梁 §6.6 提高弯曲刚度的一些措施 §6.1 工程中的弯曲变形问题 1. 实例 ①车床主轴:变形过大,会使齿轮啮合不良,轴与轴承产生非均匀磨 损,产生噪声,降低寿命,影响加工精度。 ②吊车梁:变形过大会出现小车爬坡现象,引起振动。 2. 研究变形目的 ①建立刚度条件,解决刚度问题 ②建立变形协调条件,解决超静定问题 ③为振动计算奠定基础。 §6.2 挠曲线的微分方程 1. 概念 以简支梁为例,以变形前的轴线为 x 轴,垂直向上为 y 轴,xoy 平面
为梁的纵向对称面。 ①挠曲线: Y 在对称弯曲情况下,变形后梁的轴 线为xoy平面内的一条曲线,此曲线称 f(x 为挠曲线。 ②挠度: 梁的任一截面形心的竖直位移称为挠度。 ③挠曲线的方程式: w-fx) ④转角:弯曲变形中,梁的横截面对其原来位置转过的角度0,称 为截面转角。根据平面假设,梁的横截面变形前,垂直于轴线,变形后 垂直于挠曲线。故 转角©1挠曲线的法线与轴的夹角 2.挠曲线的切线与x轴的夹角 m0架 0- y ⑤挠度w和转角9是度量弯曲 变形的两个基本量。 ds ⑥挠度与转角符号规定:在图 示坐标中,挠度向上为正, 0 】0 0+d dx 反时针的转角为正。 2.挠曲线的曲率表示式:
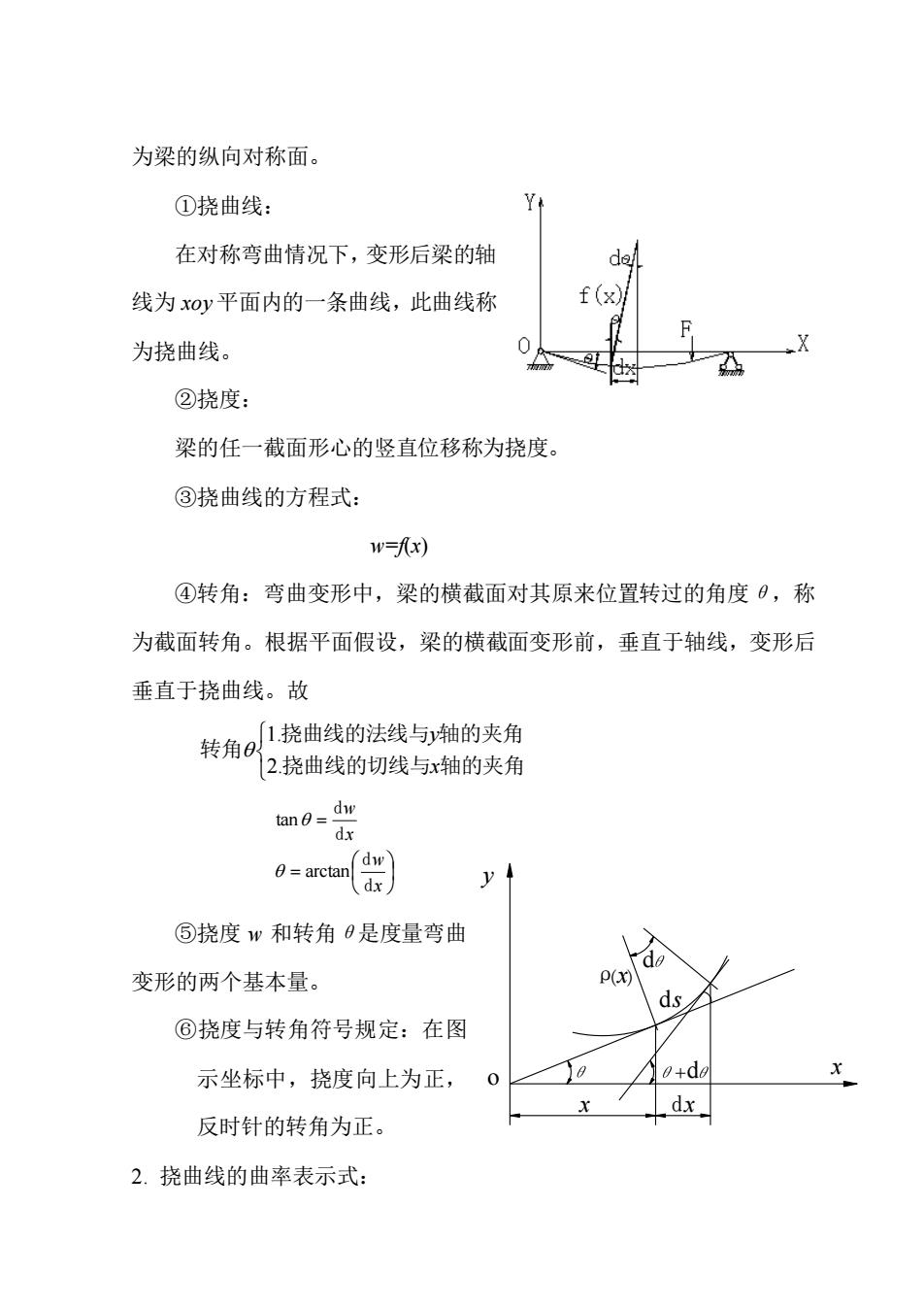
为梁的纵向对称面。 ①挠曲线: 在对称弯曲情况下,变形后梁的轴 线为 xoy 平面内的一条曲线,此曲线称 为挠曲线。 ②挠度: 梁的任一截面形心的竖直位移称为挠度。 ③挠曲线的方程式: w=f(x) ④转角:弯曲变形中,梁的横截面对其原来位置转过的角度θ,称 为截面转角。根据平面假设,梁的横截面变形前,垂直于轴线,变形后 垂直于挠曲线。故 挠曲线的切线与 轴的夹角 挠曲线的法线与 轴的夹角 转角 x y 2. 1. = = x w x w d d d d arctan tan ⑤挠度 w 和转角θ是度量弯曲 变形的两个基本量。 ⑥挠度与转角符号规定:在图 示坐标中,挠度向上为正, 反时针的转角为正。 2. 挠曲线的曲率表示式: o y x s + d ρ d ( )x d d x x
①纯弯面:。出 ②横力言角:南四 细长梁么≥5,忽略F影响。 3.挠曲线的曲率表达式 ①纯弯曲: 日台 (a) M M ②横力弯曲: M>0 M<0 对细长梁而言,忽略剪力F的影 0 <0 0 X 响 和 (b) ③高等数学中对曲率的定义 及表达式 lds pldo 1de ds dx p ds 于是式(a)转化为 doM dsEI (c) 在我们选定的坐标系内,若弯矩M为正,则挠曲线向下凸,(如图所示), 随着弧长S的增加,O也是增加的,即正增量ds对应的d8也是正的,于 是考虑符号后,式(c)可写成 (d)
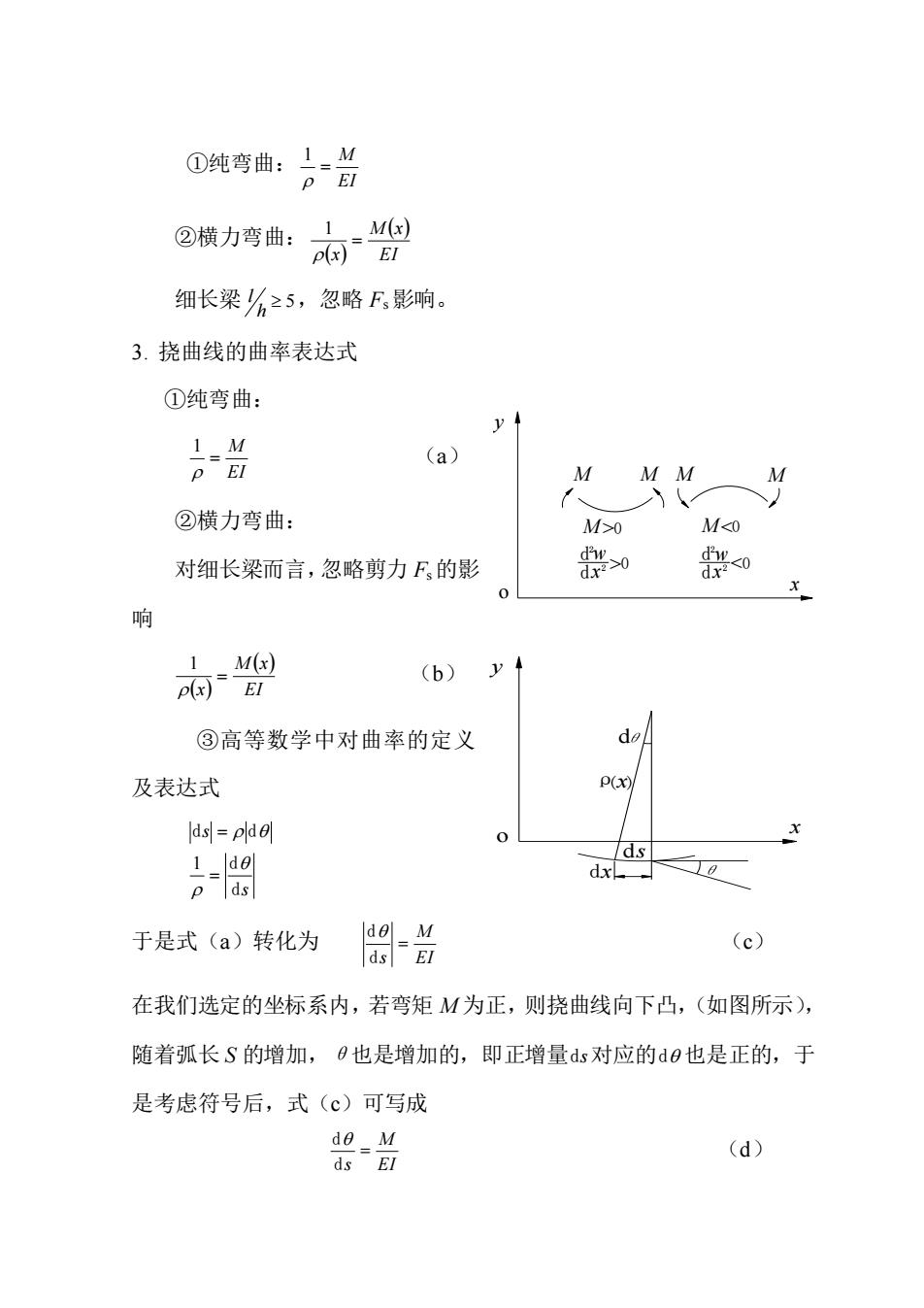
①纯弯曲: EI M = 1 ②横力弯曲: ( ) ( ) EI M x x = 1 细长梁 5 h l ,忽略 Fs 影响。 3. 挠曲线的曲率表达式 ①纯弯曲: EI M = 1 (a) ②横力弯曲: 对细长梁而言,忽略剪力 Fs 的影 响 ( ) ( ) EI M x x = 1 (b) ③高等数学中对曲率的定义 及表达式 s s d d d d = = 1 于是式(a)转化为 EI M s = d d (c) 在我们选定的坐标系内,若弯矩 M 为正,则挠曲线向下凸,(如图所示), 随着弧长 S 的增加,θ也是增加的,即正增量 ds 对应的 d 也是正的,于 是考虑符号后,式(c)可写成 EI M s = d d (d) y o x >0 <0 d 2 dx 2 >0 2 0 dx 2 d < M M M M M M w w x y o d ρ( )x ds dx

m0出 d-w = dx2 dx 1+ ds=ar+ao时-d 注意到 d ds 代入式(d)及: d2w M (e) (dw E 此为挠曲线的微分方程,适用于弯曲变形的任意情况,它是非线性的。 在小变形的情况下,梁的挠度w一般都远小于跨度,挠曲线w=f是一 非常平坦的曲线,转角日也是一个非常小的角度,于是 0em0-张=8 (f) 式(e)中(a,于是式(e)可写成 d'w M dx?EI (g) 此式为挠曲线的近似微分方程
x w d d tan = s x x w s x x s x d d d d d d d d d d d d = = arctan s x x w x w d d d d d d 2 2 2 1 + = 注意到 ( ) ( ) 3 2 d d d d d d d d d d d d + = = + = + 2 2 2 2 2 2 1 1 x w x w s x x w s x w 代入式(d)及: EI M x w x w = + 3 2 2 2 2 1 d d d d (e) 此为挠曲线的微分方程,适用于弯曲变形的任意情况,它是非线性的。 在小变形的情况下,梁的挠度 w 一般都远小于跨度,挠曲线 w=f(x)是一 非常平坦的曲线,转角θ也是一个非常小的角度,于是 f (x) x w tan = = ' d d (f) 式(e)中 1 2 x w d d ,于是式(e)可写成 EI M x w = 2 2 d d (g) 此式为挠曲线的近似微分方程

§6.3用积分法求弯曲变形 1.挠曲线的近似微分方程 d2w M X=a,W=0 dx2EI 对等直梁而言,E1为常量,于是上式可写成0 a胺=M x=b,W=0 a 积分可得转角方程,再积分可得挠曲线方程0 sc y 以 X=C,W=0 Ehw=∫[MxHr+Cx+D a 式中C,D为积分常数,可由边界条件及连0 续条件确定。 2.边界条件: 在挠曲线的某些点上,挠度或转角有时是已知的这类条件称为边界 条件。 3.连续条件: 挠曲线是一条光滑连续的曲线,在挠曲线的任一点上有唯一确定的 挠度和转角这就是连续条件。 4.刚度条件: hwls [w]l lol.s[] Examplel.EJ=const
§6.3 用积分法求弯曲变形 1. 挠曲线的近似微分方程 EI M x w = 2 2 d d 对等直梁而言,EI 为常量,于是上式可写成 M x w EI = 2 2 d d 积分可得转角方程,再积分可得挠曲线方程 = M x + C x w EI d d d EIw = Mdx dx + Cx + D 式中 C、D 为积分常数,可由边界条件及连 续条件确定。 2. 边界条件: 在挠曲线的某些点上,挠度或转角有时是已知的这类条件称为边界 条件。 3. 连续条件: 挠曲线是一条光滑连续的曲线,在挠曲线的任一点上有唯一确定的 挠度和转角这就是连续条件。 4. 刚度条件: t w w w x m x Example1. EI=const x x x a o y a a o o y y =0 =c, =0 =b, =0 x=a, =0 x x