
LMS adaptive wiener filter LMS principles: The mean-square value of the error between the output of linear components and the desired response reaches the minimum value. 11
11 LMS adaptive wiener filter LMS principles: The mean-square value of the error between the output of linear components and the desired response reaches the minimum value
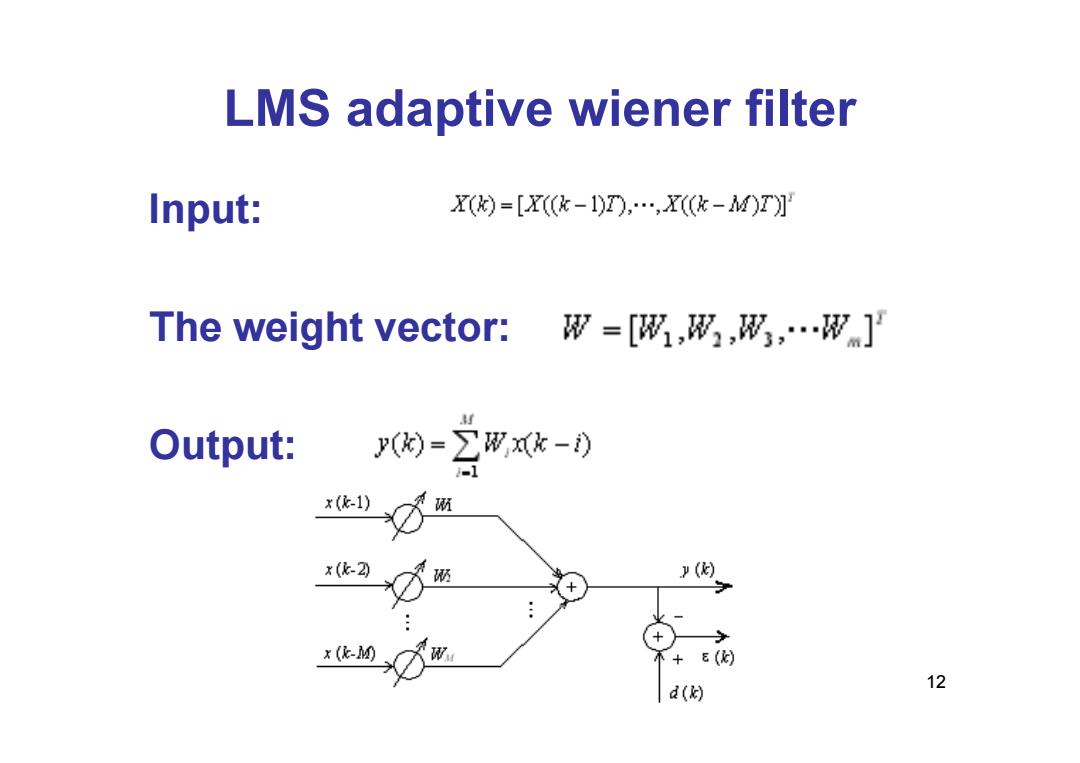
LMS adaptive wiener filter Input: X(k)=[X(-1)),…,X(k-M)T] The weight vector: 形=[形1,形,形,…W] Output:(=2形k-) x(依1) x(k-2 硒 () + x(民-0 E() d() 12
12 LMS adaptive wiener filter Input: The weight vector: Output:

x(k1) x(化2 y(k) Define the error signal: x(k-M) 不+E() ()=d)-(t) d() =d()-∑wX(k-) -1 Its vector expression is a(k)=a(k-WX(k =d(k-X'(k The square value of the error: E2()=d2()-2d()X'(kW+WX()X'()形 13
13 Define the error signal: Its vector expression is The square value of the error :

e2()=d()-2d)X(kW+W'X()X()W Taking mathematical expectation,the mean- square error is E{E()=E{d'()}-2E{ak)X(k)}W+WE{X()X'(k)}W Define cross-correlation function vector and auto-correlation function matrix: R=Ed(k)x(k) Ra=E{X()X()》 The mean-square error can be represented as: Es(k=Ed'(k-2RW+WRoW 14
14 Taking mathematical expectation ,the mean – square error is Define cross-correlation function vector and auto-correlation function matrix: The mean-square error can be represented as:
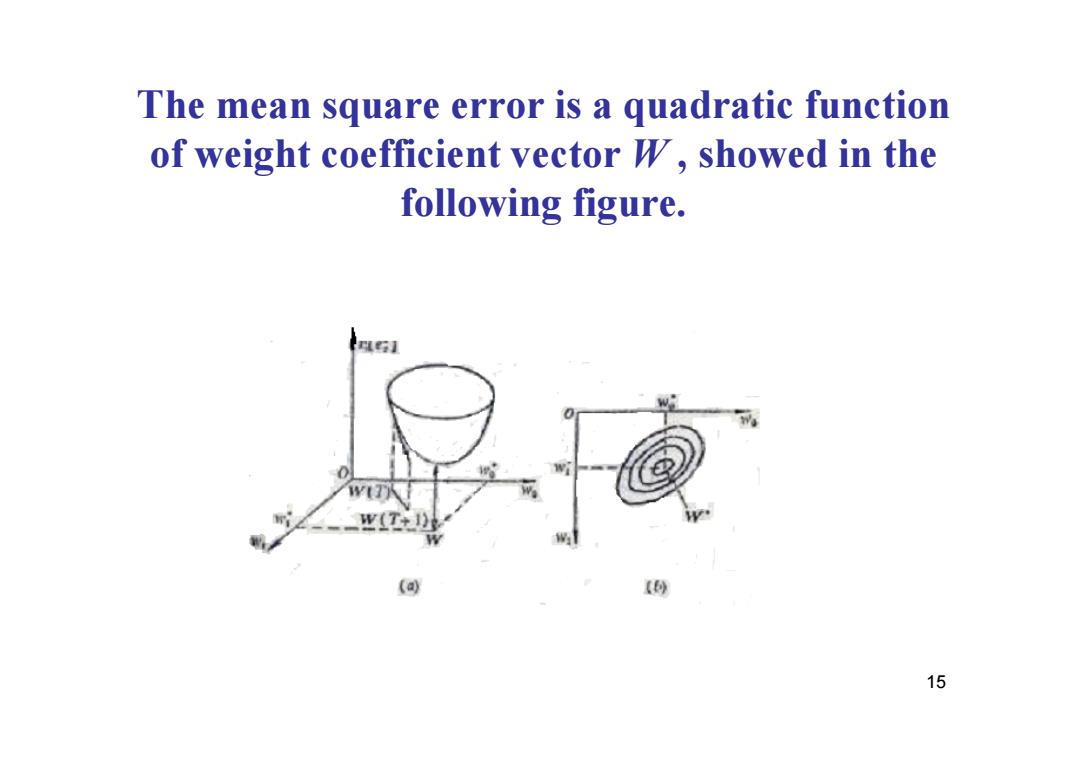
The mean square error is a quadratic function of weight coefficient vector W,showed in the following figure. w wLT中 W ( (约 15
15 The mean square error is a quadratic function of weight coefficient vector W , showed in the following figure