
卫生/医学统计学实习指导(®2.1x版)实习2计数资料的描述7门 >(x<-p0133an,tet(x=4,T=120*0.008)】 Exact Poisson test data: 41 me base:1200.008 number of events =4,time base =0.96,p-value =0.01663 1.13527610.668322 sample escimates: 4.166667 泊松分布近似法求得的率的可信区间 0.088902679 vel") 110.95 (曾庆、彭斌)
卫生/医学统计学实习指导(R2.1x 版) /实习 2 计数资料的描述 7/7 泊松分布近似法求得的率的可信区间 (曾庆、彭斌)
卫生医学统计学实习指导(R2.x版实习3参数估计和t检验1口 实习3参数估计和t检验 一、目的与要求 1、掌握抽样误差的概念及计算方法 2、掌握参数估计的概念及方法: 3、掌握可信区间的意义及估计方法: 4、掌握t检验的概念、应用条件和不同设计类型的t检验 学时 3学时 三、实验步骤 1、2005年某市城镇8岁男孩握力(Kg)测验结果如表31所示。 表3-1120例8岁男孩程力(Kg)测验结果 8.6 10 146 13.5 150 0 11.2 112 17.5 9.2 84 12.8 8.6 11.0 8.6 9.7 13.5 16.8 11.1 12.5 10.5 120 8.0 110 12.0 7.0 14.0 11.5 13.5 65 15.0 12.2 115 11.g 11.4 13.5 11.3 15.0 134 142 11.3 8.0 .2 12 64 13 4 10.0 12. 14.0 8.2 14.6 10.0 11. 3 10.0 10.4 12.4 96 13 112 11.0 12.4 9.5 10.3 155 125 9 12 113 87 102 11.3 12.4 94 102 12. 12.0 150 97 1 10.0 11.5 120 97 120 13.5 7.5 25 10s 16.0 98 10.0 11.5 7.4 问题1:计算均数及标准差?抽样误差是多少? 问顾2:估计8岁男孩据力的95%参考值范围及95%可信区间?并讲行比较? 问题3:将上表中的120个握力测验数据当作 个总体,从中进行随机抽样,样本含量为30 共抽10 个样本 计算每个样本的均数及标准差 与总体均数及标准差进行比较,解释二者 之间的差异:每次抽样的抽样误差大小是多少? 第1小题R参考程序 R计算程序 程序解释 x<-scan(textConnection(" 数据输入程序:数据保存在列表x中。scan( 8.610.714.613.515.09.415.514.011.211.2 函数顺序读取输入数据,其结果是生成列表 1759284128861108697135168111 对象,这里是x。函数unlist0将列表对象转 12.510.512.0801101207.014.011.513.5 换为普通数值向量。 6515012211511911413511315013 134142113809212.58.56.410.311 11.212.09.010.013.511.47.413.211.810.0 12.57.514.08.214.610.011.58.510.010.4 12.49.613.211.25.511.012.49.510.315.5 259072112998710211312413294 10.212.210.514.512.015.09.76.37.110.0
卫生/医学统计学实习指导(R2.1x 版)/实习 3 参数估计和 t 检验 1/7 实习 3 参数估计和 t 检验 一、目的与要求 1、 掌握抽样误差的概念及计算方法; 2、 掌握参数估计的概念及方法; 3、 掌握可信区间的意义及估计方法; 4、 掌握 t 检验的概念、应用条件和不同设计类型的 t 检验。 二、学时 3 学时。 三、实验步骤 1、 2005 年某市城镇 8 岁男孩握力(Kg)测验结果如表 3-1 所示。 表 3-1 120 例 8 岁男孩握力(Kg)测验结果 8.6 10.7 14.6 13.5 15.0 9.4 15.5 14.0 11.2 11.2 17.5 9.2 8.4 12.8 8.6 11.0 8.6 9.7 13.5 16.8 11.1 12.5 10.5 12.0 8.0 11.0 12.0 7.0 14.0 11.5 13.5 6.5 15.0 12.2 11.5 11.9 11.4 13.5 11.3 15.0 13.5 13.4 14.2 11.3 8.0 9.2 12.5 8.5 6.4 10.3 11.5 11.2 12.0 9.0 10.0 13.5 11.4 7.4 13.2 11.8 10.0 12.5 7.5 14.0 8.2 14.6 10.0 11.5 8.5 10.0 10.4 12.4 9.6 13.2 11.2 5.5 11.0 12.4 9.5 10.3 15.5 12.5 9.0 7.2 11.2 9.9 8.7 10.2 11.3 12.4 13.2 9.4 10.2 12.2 10.5 14.5 12.0 15.0 9.7 6.3 7.1 10.0 10.1 11.5 9.8 7.8 12.0 9.7 12.0 10.0 13.5 7.5 12.5 10.5 16.0 9.8 10.0 11.5 14.0 7.4 问题 1:计算均数及标准差?抽样误差是多少? 问题 2:估计 8 岁男孩握力的 95%参考值范围及 95%可信区间?并进行比较? 问题 3:将上表中的 120 个握力测验数据当作一个总体,从中进行随机抽样,样本含量为 30, 共抽 10 个样本。计算每个样本的均数及标准差;与总体均数及标准差进行比较,解释二者 之间的差异;每次抽样的抽样误差大小是多少? 第 1 小题 R 参考程序 R 计算程序 程序解释 x<-scan(textConnection(" 8.6 10.7 14.6 13.5 15.0 9.4 15.5 14.0 11.2 11.2 17.5 9.2 8.4 12.8 8.6 11.0 8.6 9.7 13.5 16.8 11.1 12.5 10.5 12.0 8.0 11.0 12.0 7.0 14.0 11.5 13.5 6.5 15.0 12.2 11.5 11.9 11.4 13.5 11.3 15.0 13.5 13.4 14.2 11.3 8.0 9.2 12.5 8.5 6.4 10.3 11.5 11.2 12.0 9.0 10.0 13.5 11.4 7.4 13.2 11.8 10.0 12.5 7.5 14.0 8.2 14.6 10.0 11.5 8.5 10.0 10.4 12.4 9.6 13.2 11.2 5.5 11.0 12.4 9.5 10.3 15.5 12.5 9.0 7.2 11.2 9.9 8.7 10.2 11.3 12.4 13.2 9.4 10.2 12.2 10.5 14.5 12.0 15.0 9.7 6.3 7.1 10.0 数据输入程序;数据保存在列表 x 中。scan() 函数顺序读取输入数据,其结果是生成列表 对象,这里是 x。函数 unlist()将列表对象转 换为普通数值向量

卫生/医学统计学实习指导(R2.1x版实习3参数估计和t检验27 10.111.59.87.812.09.712.010.013.57.5 12.510.516.09.810.011.514.07.4" what=list(0) x<-unlist(x) 在输出窗口显示输入的数据 summary(x) 计算抽要统计量 n<-length(x 计算例数 mean(x);sd(x 均数、标准差 sd(x sart(n) 计算标准误 ci<-t.test(x.conf.level =0.95) 利用Ltesti计算可信区间,conflevel=指定可 信区间大小 显示总体均数95%可信区间 mean.ci<-function(x) 将以上计算过程整理为计算函数mean.ci0, (n<-length(x):m<-mean(x);sd<-sd(x) 以方便使用。参数x为待计算的量。 se<-sd(x)/sqrt(n) ci<-unlist(t.te [4JD) cbind(n mean=m,sd,std.err-se,LCI-ci[l UCI=ei2D) mean ci(x) 使用mean.ciO函数计算以上结果 set.seed(13579) 设定随机种子号13579 x.sampsapply(1:10,function(i)sample(x 从120 个数据中进行随机抽样, 简单随机 30) (无放回),抽样10个样本 每个样本 量30,抽样结果保存在矩阵对象X.samD中 x samn 显示抽样结果 mean.ci(c(x.samp)) 计算全部样本的例数、均数、标准差 data frame( samp,2,mean.cij) 针算标准误、计算可信区间 names(x.r水-c(例数,均 ,标准差,标误 十算各个样本的相应结果 95%可信限下限',95%可信限上限 设计表头以方便阅读 显示结果 names(x.r)<c('n,'mean','sd','se','lci','uci) 重新设计变量名以方便绘图命令 plot(x.r5mean.ylim-c(9.5.13).ylab 样本均数 绘制各个样本的均数 ,xlab=样本) abline(h=mean(x)) 增加总体均数位置线 lines(x rSlci) 增加可行区间下限,增加可行区间上限,将 lines(x rSuci 可信区间绘制为条形范围表示。 hist(x.rSm xlab-'握力(Kgy,main=样本均 绘制样本均数的直方图 数的直方图 abline(v=mean(x).Iwd=2) 添加总体均数参考线 plot(x.$mean,ylim-c(9.5,l3),ylab=样本均数绘制各个样本的均数 .xlab=样本) abline h ean(x)) 增加总体均数位置线 t<-lapply(1:10.function(i) 将可信区间绘制为条形范围表示
卫生/医学统计学实习指导(R2.1x 版)/实习 3 参数估计和 t 检验 2/7 10.1 11.5 9.8 7.8 12.0 9.7 12.0 10.0 13.5 7.5 12.5 10.5 16.0 9.8 10.0 11.5 14.0 7.4"), what=list(0)) x<-unlist(x) x 在输出窗口显示输入的数据 summary(x) n<-length(x) mean(x);sd(x) sd(x)/sqrt(n) ci<-t.test(x, conf.level = 0.95) ci$conf.int mean.ci<-function(x) {n<-length(x); m<-mean(x) ; sd<-sd(x) se<-sd(x)/sqrt(n) ci<-unlist(t.test(x)[[4]]) cbind(n, mean=m, sd,std.err=se, LCI=ci[1], UCI=ci[2]) } mean.ci(x) 计算摘要统计量 计算例数 均数、标准差 计算标准误 利用 t.test()计算可信区间,conf.level=指定可 信区间大小 显示总体均数 95%可信区间 将以上计算过程整理为计算函数 mean.ci(), 以方便使用。参数 x 为待计算的量。 使用 mean.ci()函数计算以上结果 set.seed(13579) x.samp <- sapply(1:10, function(i) sample(x, 30) ) x.samp 设定随机种子号 13579 从 120 个数据中进行随机抽样,简单随机抽 样(无放回),抽样 10 个样本,每个样本含 量 30,抽样结果保存在矩阵对象 x.samp 中 显示抽样结果 mean.ci(c(x.samp)) x.r<-data.frame( t(apply(x.samp,2,mean.ci)) ) names(x.r)<-c('例数', '均数', '标准差', '标准误', '95%可信限下限', '95%可信限上限') x.r 计算全部样本的例数、均数、标准差 计算标准误、计算可信区间 计算各个样本的相应结果 设计表头以方便阅读 显示结果 names(x.r) <- c('n', 'mean', 'sd', 'se', 'lci', 'uci') plot(x.r$mean, ylim=c(9.5,13), ylab='样本均数 ', xlab='样本') abline(h=mean(x) ) lines(x.r$lci) lines(x.r$uci) hist(x.r$mean,xlab='握力(Kg)',main='样本均 数的直方图') abline(v=mean(x),lwd=2) 重新设计变量名以方便绘图命令 绘制各个样本的均数。 增加总体均数位置线 增加可行区间下限,增加可行区间上限,将 可信区间绘制为条形范围表示。 绘制样本均数的直方图 添加总体均数参考线 plot(x.r$mean, ylim=c(9.5,13), ylab='样本均数 ', xlab='样本') abline(h=mean(x) ) t<-lapply(1:10,function(i) 绘制各个样本的均数 增加总体均数位置线 将可信区间绘制为条形范围表示

卫生医学统计学实习指导(R2.1x版/实习3参数估计和t检验3门 lines(c(i,i).t(x.rfi,5:6)).type=1)) 2、某研究人员研究某种治疗糖尿病的新型药物的疗效,用传统标准药作对照,两组分别 察了15例病人,记录用药前及用药后3周的症状积分如表3-2所示。 表32两种药物治疗糖尿病定状积分变化数据 药物观察时间123456789101112131415 新药 用药前 161723162619221623222533221722 用药后 6 75576607997627 传统药用药前222218161918142815273024282225 用药后14101091012111210412134108 问题1:分别计算每一组用药前后的症状积分 问题2:用药前后新药的症状积分有无变化?传统药有无变化? 问题3:新药与传统药的症状改普有无差异? 第2小题R参考程序 R计算程疗 程序解释 x1<-c16,17,23,16,26,19,22,16,23,22,25,33,22,17,22)数据输入程序:数据集保存为向量的形 x2<-c6,7,55,7,6,6,0,7,9.9,7.6.2,7 式。x1,x2,y1,v2分别对应两组前后 v1<.c22.22.1816.19.1814281527.30242822.25 的数据。 y2<-c14,10,10,9,10,12,11,12,10,412,13,4,10,.8) cbind(x1,x2);cbind(y1,y2) 在输出窗口显示输入的数据 summary(xI);mean.ci(xl) 计算描述性统计量 summary(x2)mean ci(x2) summary(y1).mean.ci(y1) summary2 mean.i02 lapply(list(g=x1-x2.group2=y1-y2).summary) 两组差值的描述统计量 lapply(list(g=x1-x2.group2-y1-y2),mean.ci) ttest(x1 x2.paired=T) 使用tttest)进行配对t检验,指定配对 t.test(y1,y2,paired=T) 变量,按两种药物分别分析 var.test(xl-x2,yl-y2 进行两种药物疗效的t检验,先进行方 ttest(x1-x2.yl-y2) 差齐性检验,然后做1检验 四、评价 1、第1小题R运行主要结果 原样本的抽样描述统计量结果 mean.ci(x) mean sd std.err LCI UCI [1,】12011.128332.4198470.220900810.6909311.56574 抽样运行结果(注,可以采用机器时间作为随机种子,这样每次运行结果都会不同)。 全部样本的抽样描述统计量结果
卫生/医学统计学实习指导(R2.1x 版)/实习 3 参数估计和 t 检验 3/7 lines(c(i,i),t(x.r[i,5:6]),type='l') ) 2、 某研究人员研究某种治疗糖尿病的新型药物的疗效,用传统标准药作对照,两组分别观 察了 15 例病人,记录用药前及用药后 3 周的症状积分如表 3-2 所示。 表 3-2 两种药物治疗糖尿病症状积分变化数据 药物 观察时间 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 新药 用药前 16 17 23 16 26 19 22 16 23 22 25 33 22 17 22 用药后 6 7 5 5 7 6 6 0 7 9 9 7 6 2 7 传统药 用药前 22 22 18 16 19 18 14 28 15 27 30 24 28 22 25 用药后 14 10 10 9 10 12 11 12 10 4 12 13 4 10 8 问题 1:分别计算每一组用药前后的症状积分。 问题 2:用药前后新药的症状积分有无变化?传统药有无变化? 问题 3:新药与传统药的症状改善有无差异? 第 2 小题 R 参考程序 R 计算程序 程序解释 x1<-c(16,17,23,16,26,19,22,16,23,22,25,33,22,17,22) x2<-c(6,7,5,5,7,6,6,0,7,9,9,7,6,2,7) y1<-c(22,22,18,16,19,18,14,28,15,27,30,24,28,22,25) y2<-c(14,10,10,9,10,12,11,12,10,4,12,13,4,10,8) 数据输入程序;数据集保存为向量的形 式。x1,x2,y1,y2 分别对应两组前后 的数据。 cbind(x1,x2); cbind(y1,y2) 在输出窗口显示输入的数据 summary(x1);mean.ci(x1) summary(x2);mean.ci(x2) summary(y1);mean.ci(y1) summary(y2);mean.ci(y2) lapply(list(g=x1-x2,group2=y1-y2),summary) lapply(list(g=x1-x2,group2=y1-y2),mean.ci) 计算描述性统计量 两组差值的描述统计量 t.test(x1, x2, paired=T) t.test(y1, y2, paired=T) 使用 t.ttest()进行配对 t 检验,指定配对 变量,按两种药物分别分析 var.test(x1-x2,y1-y2) t.test(x1-x2,y1-y2) 进行两种药物疗效的 t 检验,先进行方 差齐性检验,然后做 t 检验 四、评价 1、第1小题R运行主要结果 原样本的抽样描述统计量结果 抽样运行结果(注:可以采用机器时间作为随机种子,这样每次运行结果都会不同)。 全部样本的抽样描述统计量结果
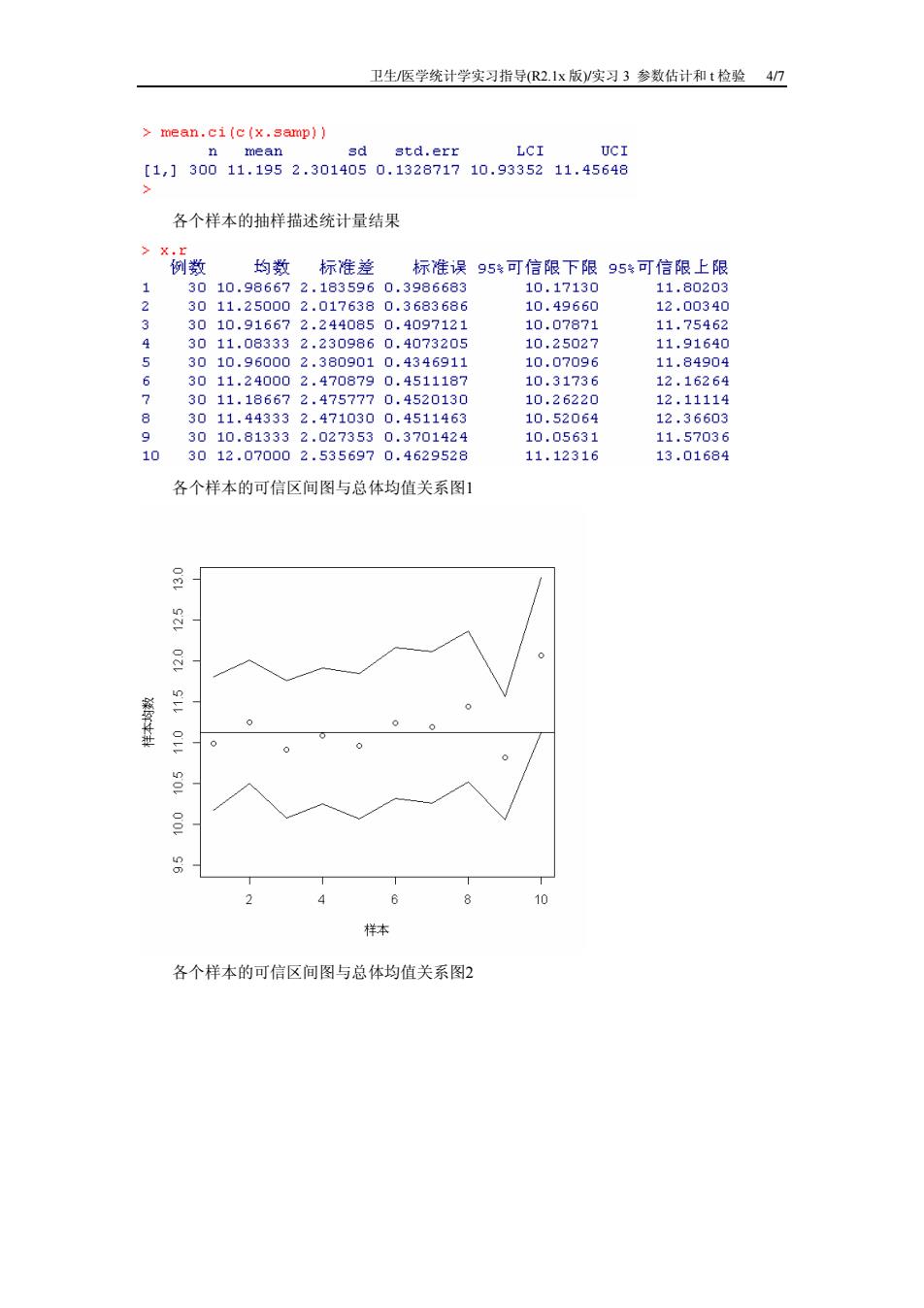
卫生/医学统计学实习指导(R2.1x版/实习3参数估计和t检验4/7 >mean.ci(c(x.samp)) 1306465230a65o.5s5n.9351.4s 各个样木的抽样描述统计量结果 例数 均数 标准差 标准误95可信限下限95可信限上限 10.17130 10078 456 11.083332.2309860.407320 10.2502 11.91640 624708798: 0.37 12626 10.26220 12.1111 813332 73530. 66u 10 3012.070002.5356970.4629528 11.12316 13.01684 各个样本的可信区间图与总体均值关系图1 4 样本 各个样本的可信区间图与总体均值关系图
卫生/医学统计学实习指导(R2.1x 版)/实习 3 参数估计和 t 检验 4/7 各个样本的抽样描述统计量结果 各个样本的可信区间图与总体均值关系图1 各个样本的可信区间图与总体均值关系图2