3.5采样时钟与采样精度的关系 3.5.2时钟抖动与相位噪声 >抖动的有效值表示 2 L() 相位噪声谱L(f-f)=10log[S.(f)/S(f)】 其中L(f)=10log[S(f)] S(f) L(f-f) 可由频谱仪近似测得。 时钟信号的功率谱密度
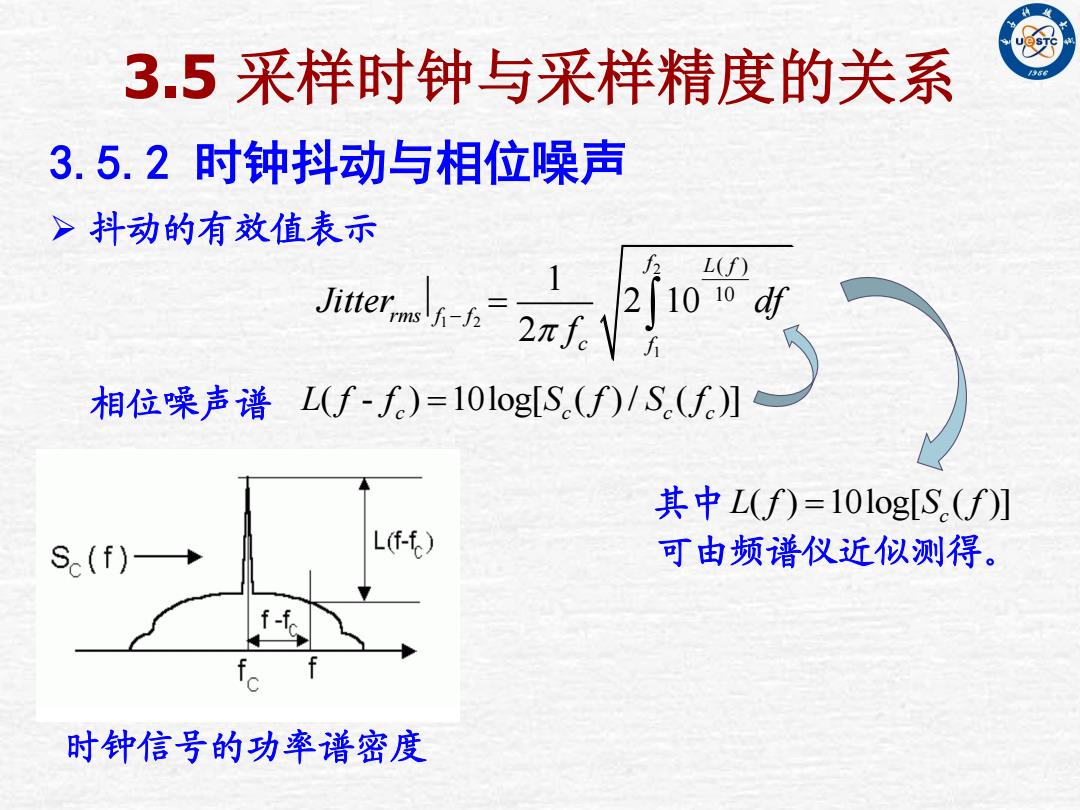
3.5 采样时钟与采样精度的关系 3.5.2 时钟抖动与相位噪声 ( - ) 10log[ ( ) / ( )] L f f S f S f c c c c 时钟信号的功率谱密度 2 1 2 1 ( ) 10 1 2 10 2 f L f rms f f c f Jitter df f 抖动的有效值表示 相位噪声谱 ( ) 10log[ ( )] 其中 L f S f c 可由频谱仪近似测得

3.5采样时钟与采样精度的关系 3.5.2时钟抖动与相位噪声 >抖动的有效值表示 1 2 L( 21010 2元f1 d >若L(f)以频率对数为横轴,Jitter可以采用分段线性近似得到 L(f) 5 -a- Jitterrms a1 2πf. : : : b3 : a3 log(f) 注1:在不同的应用场合,所关心的积分范 f2 :f4 围会有所不同。在数据采集系统中,工程 相位噪声谱函数 上一般取积分范围在10kHz到30MHz之间 注2:虽然近载波噪声属于影响系统的重要组成部分,但是在影响ADC噪声性能方面是可以忽略的
3.5 采样时钟与采样精度的关系 3.5.2 时钟抖动与相位噪声 2 1 2 1 ( ) 10 1 2 10 2 f L f rms f f c f Jitter df f 抖动的有效值表示 若 L f ( ) 以频率对数为横轴, Jitterrms 可以采用分段线性近似得到 1 1 10 10 10 1 1 1 1 10 10 10 10 1 1 1 2 10 10 2 1 2 10 1 [ ] 2 10 i i i i i i i i b a a f N rms i c i f N b a a a i i i i c i Jitter f df f a f f f f 注1:在不同的应用场合,所关心的积分范 围会有所不同。在数据采集系统中,工程 相位噪声谱函数 上一般取积分范围在10kHz到30MHz之间 注2:虽然近载波噪声属于影响系统的重要组成部分,但是在影响ADC噪声性能方面是可以忽略的
3.5采样时钟与采样精度的关系 3.5.3时钟抖动对ADC的影响 >时钟抖动对采样的表现 √ 采样精度的两个重要指标:SNR和有效位数 √ 受时钟质量影响一采样误差 X2(t) Xi(t) 时钟抖动就是对信 号幅度采样的误差 △V1 时钟抖动越大,信 电压误差 号采样的幅度误差 也越大 同样的时钟抖动, 时钟抖动 信号频率越高,采 △t 样幅度误差也越大 抖动引起的采样幅度误差 注:对于高分辨率采集系统来说,这种影响显得更加突出
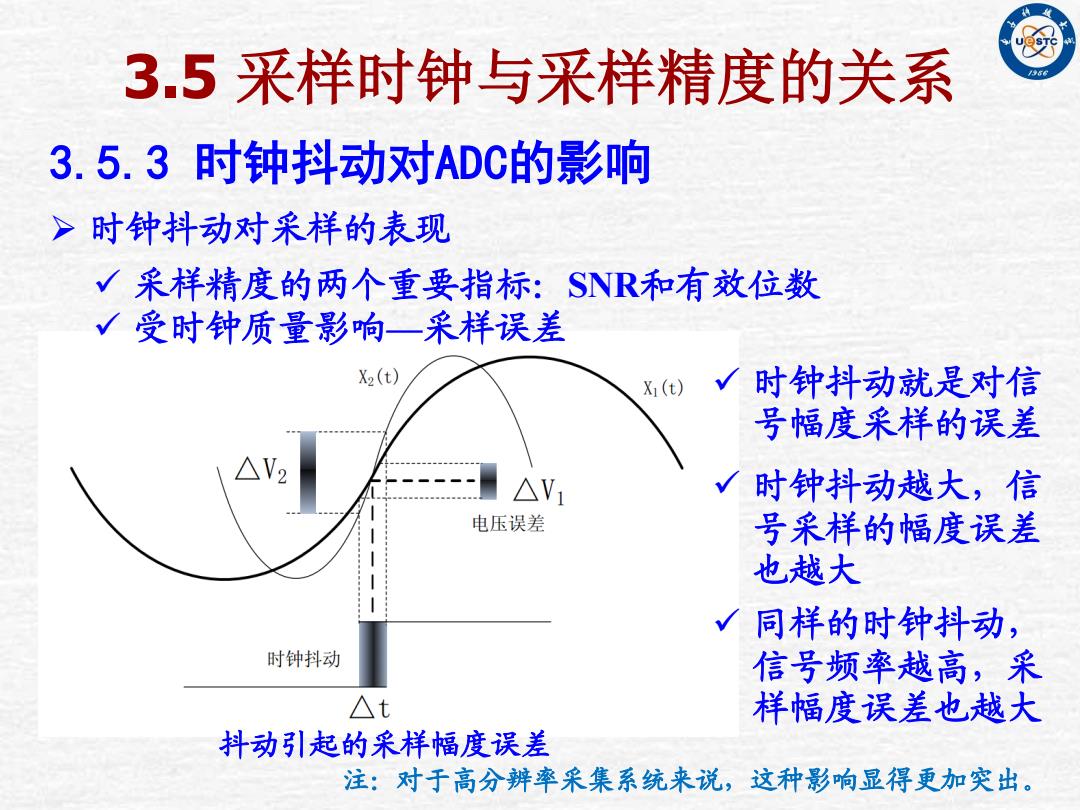
3.5 采样时钟与采样精度的关系 3.5.3 时钟抖动对ADC的影响 时钟抖动对采样的表现 注:对于高分辨率采集系统来说,这种影响显得更加突出。 时钟抖动就是对信 号幅度采样的误差 时钟抖动越大,信 号采样的幅度误差 也越大 同样的时钟抖动, 信号频率越高,采 样幅度误差也越大 采样精度的两个重要指标:SNR和有效位数 受时钟质量影响—采样误差 抖动引起的采样幅度误差
3.5采样时钟与采样精度的关系 3.5.3时钟抖动对ADC的影响 >时钟抖动对采样的表现 抖动与SNR关系 满量程信号有效值 正弦斜率 SNR=1010 P SNR=20log AV dV(@=2 fAcos2πfi dt 噪声信号有效值 X2(t) 近似计算 Xi(t) AW=2 fAcos2?πfi △V 电压误差 ↓有效值 2πfAtm 2 时钟抖动 △t A/√2 抖动引起的采样幅度误差 SNR=2010g 2πfAt,/V2 =-20log2πfiim
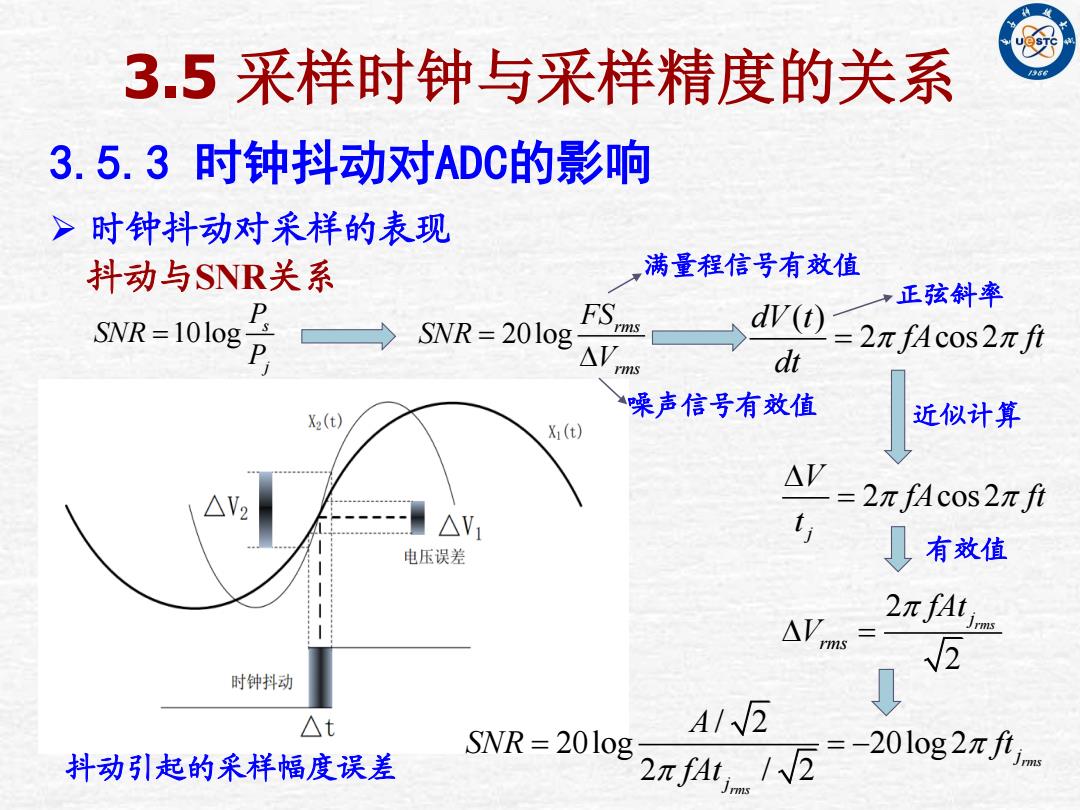
3.5 采样时钟与采样精度的关系 3.5.3 时钟抖动对ADC的影响 时钟抖动对采样的表现 10log s j P SNR P 20log rms rms FS SNR V ( ) 2 cos 2 dV t fA ft dt 2 cos 2 j V fA ft t 2 2 rms j rms fAt V / 2 20log 20log 2 2 / 2 rms rms j j A SNR ft fAt 满量程信号有效值 噪声信号有效值 正弦斜率 近似计算 有效值 抖动与SNR关系 抖动引起的采样幅度误差