3.5采样时钟与采样精度的关系 3.5.1时钟性能-抖动 1)抖动的分类 >抖动的成分:确定的、不确定的 Jitter Deterministic Jitter Random Jitter (DJ) (RJ) Data Dependent Jitter Periodic Jitter Gaussian Jitter Multiple Gaussian Jitter (DDJ) P (GJ) (MGJ) Bounded Uncorrelated Jitter (BUJ)
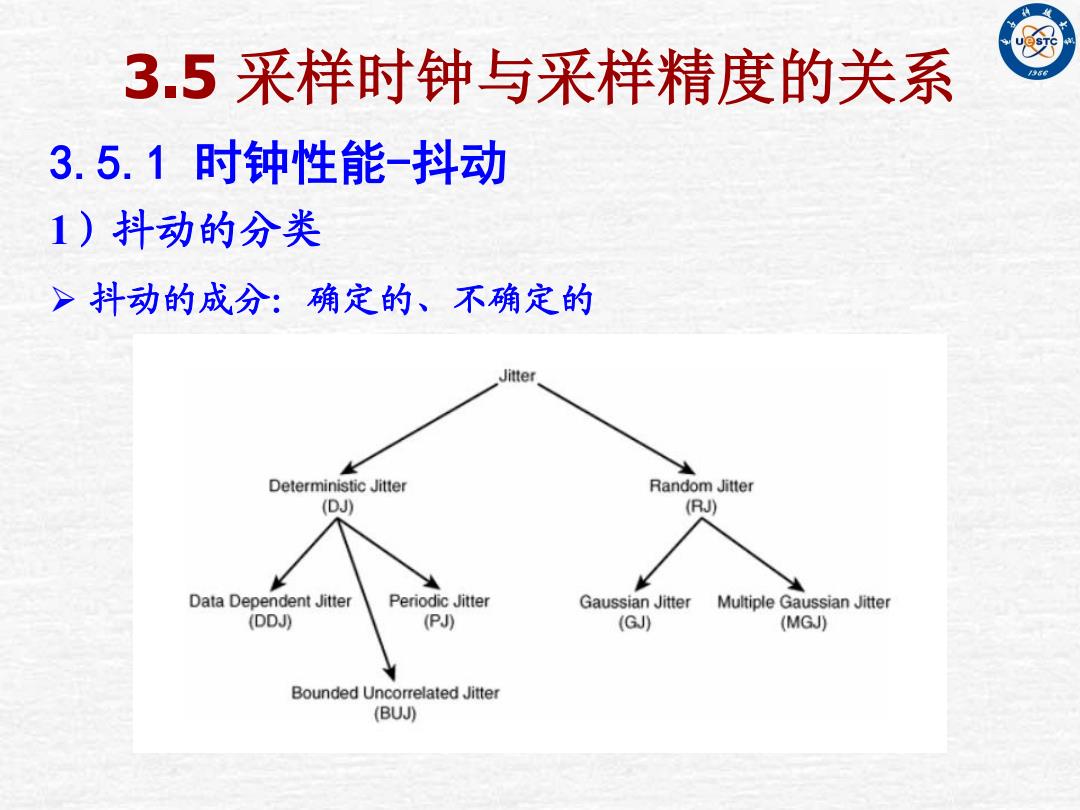
3.5 采样时钟与采样精度的关系 3.5.1 时钟性能-抖动 1)抖动的分类 抖动的成分:确定的、不确定的
3.5采样时钟与采样精度的关系 3.5.1时钟性能-抖动 2)采集系统中的时钟抖动 ∑Jiter 总周期抖动RMS:J。=1 i=l >时钟非理想性: 周期抖动PJ(Period Jitter) Jitterp =tn-tn-1-T=P2-T 周期间抖动CCJ(Cycle-.Cycle Jitter) Jitterec P3-P2 时间间隔误差TE(Time Interval Error)Jitter,=tn-nT (n-2)T (n-1)T nT (n+1)T TIE1 TIE2 TIE3 P1 理想边沿
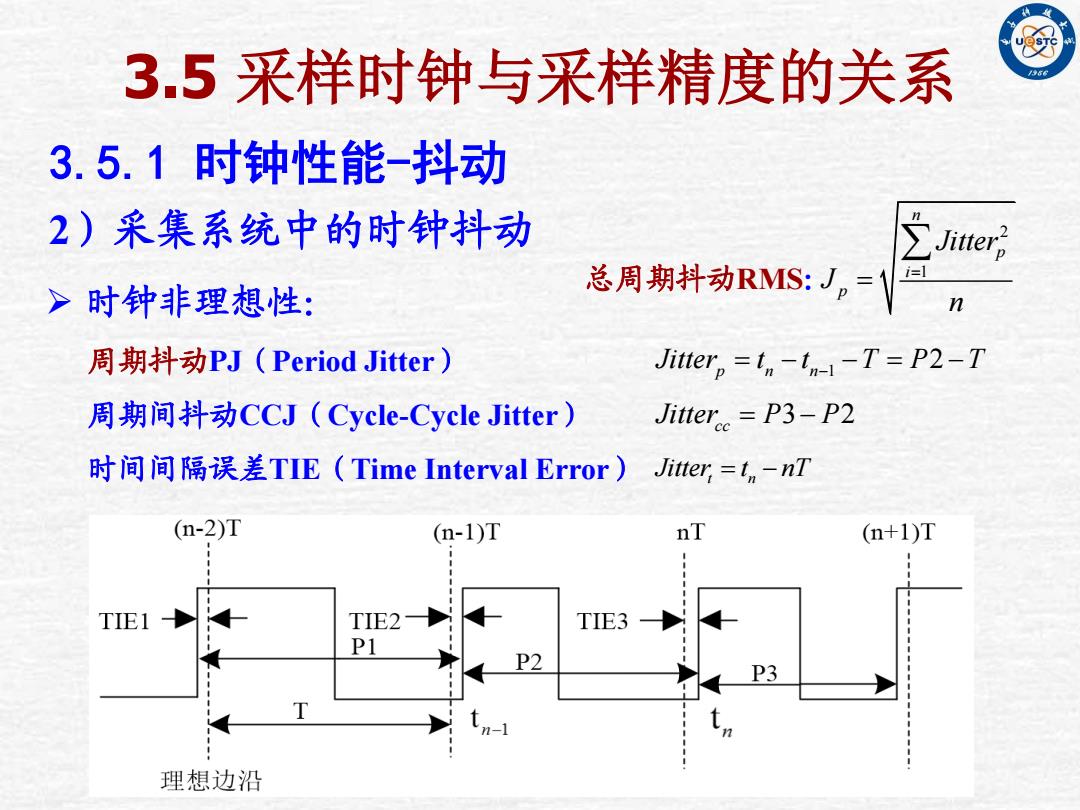
3.5 采样时钟与采样精度的关系 3.5.1 时钟性能-抖动 2)采集系统中的时钟抖动 时钟非理想性: 周期抖动PJ(Period Jitter) 周期间抖动CCJ(Cycle-Cycle Jitter) 时间间隔误差TIE(Time Interval Error) 1 2 p n n Jitter t t T P T 3 2 cc Jitter P P t n Jitter t nT 2 1 n p i p Jitter J n 总周期抖动RMS:
3.5采样时钟与采样精度的关系 3.5.1时钟性能-抖动 2)采集系统中的时钟抖动:双狄拉克模型 -Dirac functions- convolve Gaussian time(ps or UD) dual-Dirac PDF Tj=a(BER)*Rj+Dj(66) (1) Dj66)→
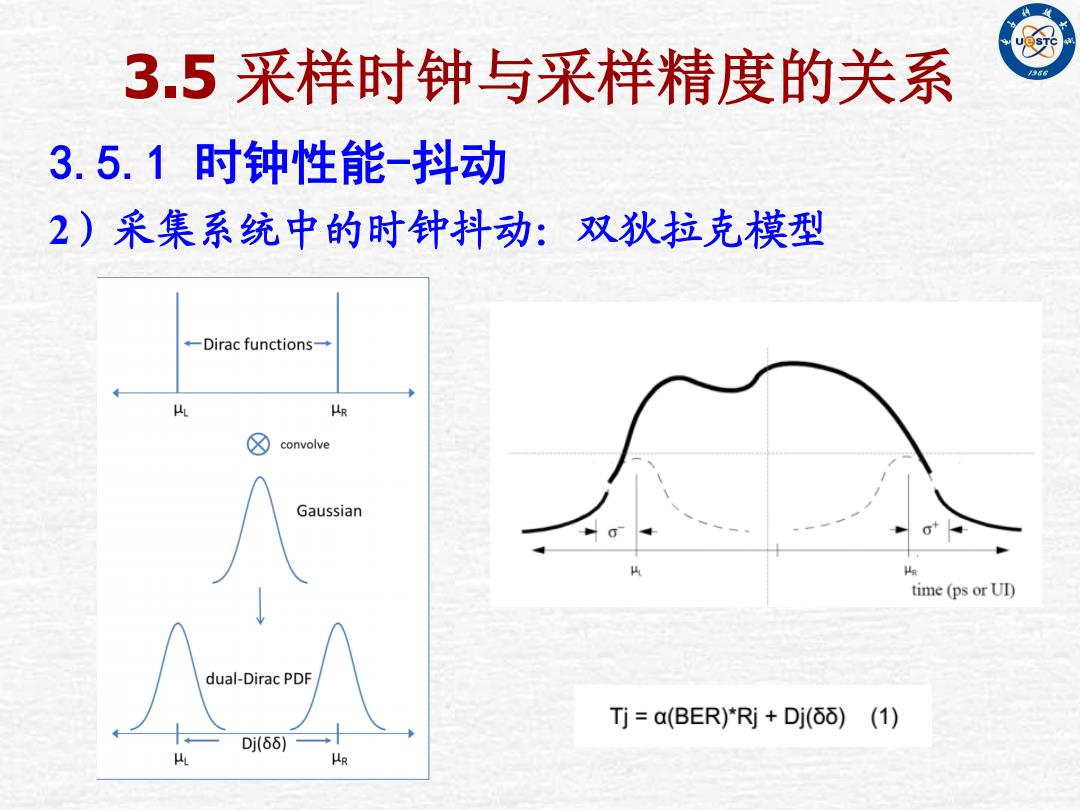
3.5 采样时钟与采样精度的关系 3.5.1 时钟性能-抖动 2)采集系统中的时钟抖动:双狄拉克模型

3.5采样时钟与采样精度的关系 3.5.2时钟抖动与相位噪声 >抖动和相位噪声都是时钟短期不稳定性的表征,这种不稳定 在时域内用时钟抖动表征,在频域内用相位噪声表征。 >相位噪声是对信号在频域变化的一种测量方式,表征时钟信 号频率的稳定度。 相位噪声定义:是指偏离载波频率(f-c)处1Hz带宽内噪声 功率与载波信号总功率的比值 1Hz带宽内相位噪声功率 L() dBc/Ha 载波总功率 时域的均方根抖动和频域的相位噪声存在确定的关系,可以由 频域的相位噪声曲线计算得到
3.5 采样时钟与采样精度的关系 3.5.2 时钟抖动与相位噪声 抖动和相位噪声都是时钟短期不稳定性的表征,这种不稳定 在时域内用时钟抖动表征,在频域内用相位噪声表征。 相位噪声是对信号在频域变化的一种测量方式,表征时钟信 号频率的稳定度。 1Hz L f dBc Hz ( ) / 带宽内相位噪声功率 载波总功率 相位噪声定义:是指偏离载波频率(f-fc)处 1Hz 带宽内噪声 功率与载波信号总功率的比值 时域的均方根抖动和频域的相位噪声存在确定的关系,可以由 频域的相位噪声曲线计算得到

3.5采样时钟与采样精度的关系 3.5.2时钟抖动与相位噪声 >相位噪声 1Hz带宽内相位噪声功率 L(f)= dBc Hz 载波总功率 S(f)为时钟功率谱 相位噪声谱L(f-f)=10log[S.(f)/S.(f)】 S(f)为载波功率谱 由于方波信号与其基频正弦波信号的 抖动特性基本一致,故研究具有相位 Lf-f) Sc(f) 噪声的正弦波信号就可以简化对时钟 抖动的分析。 正弦波时钟信号 C(t)=Asin(2πft+e(t) 时钟信号的功率谱密度 抖动Jitter= θ(t) 2 2πf
3.5 采样时钟与采样精度的关系 3.5.2 时钟抖动与相位噪声 相位噪声 1Hz L f dBc Hz ( ) / 带宽内相位噪声功率 载波总功率 ( - ) 10log[ ( ) / ( )] L f f S f S f c c c c 时钟信号的功率谱密度 正弦波时钟信号 sin(2 ( )) C t A f t t c 抖动 ( ) ( ) 2 2 c c t t Jitter T f 相位噪声谱 由于方波信号与其基频正弦波信号的 抖动特性基本一致,故研究具有相位 噪声的正弦波信号就可以简化对时钟 抖动的分析。 ( ) c S f 为时钟功率谱 ( ) c c S f 为载波功率谱