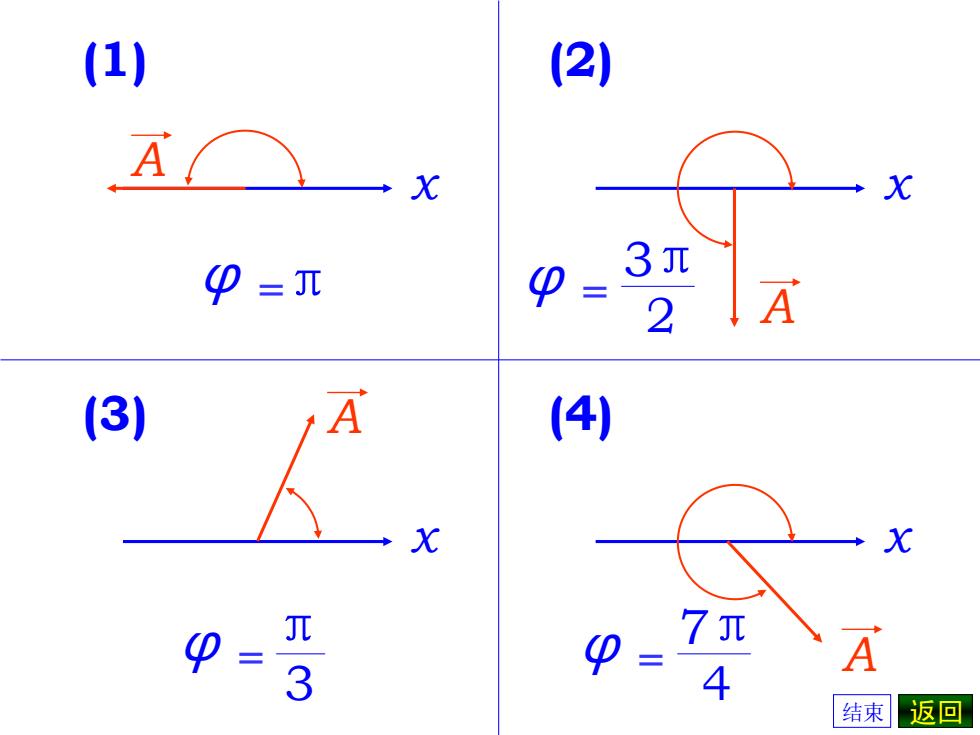
(1) 2) A X P=π 3兀 2 l A 3) (4) X X 7兀 A 3 4 结束返回
3 φ = π (3) A x φ π A = (1) x 3 2 φ = π A (2) x 7 4 φ = π A (4) x 结束 返回

15-3 一质量为10g的物体作简谐振动, 其振幅为24cm,周期为4.0s,当t=0时, 位移为+24cm。求: (1)t=0.5s时,物体所在位置; 2)t=0.5s时,物体所受力的大小与方向; (3)由起始位量运动x=12cm处所需的最少 时间; (4)在x=12cm处,物体的速度、动能以及 系统的势能和总能量。 结束返回
15-3 一质量为10g的物体作简谐振动, 其振幅为24cm,周期为4.0s,当t =0时, 位移为+24cm。求: (1) t =0.5s时,物体所在位置; (2) t =0.5s时,物体所受力的大小与方向; (3)由起始位量运动x = l2cm处所需的最少 时间; (4)在x=12cm处,物体的速度、动能以及 系统的势能和总能量。 结束 返回

解:A=0.24mw= 2元 2元 兀 T 4 2 =1.57s1 xo=A=0.24m t=0 振动方程为:x=0.24cos2 t=0.5s x=0.24c0s2×0.5) =0.24c0S0.25π 2 =0.24× 2 =0.17m 结束返回
t =0 ω 2π T = 4 =1.57s-1 = 2 = 2π π v 0 = 0 x 0 = A =0.24m x =0.24 cos t 2 π t =0.5s x =0.24 cos( × ) 2 π 0.5 =0.24 cos0.25π × =0.17m 2 2 =0.24 振动方程为: 解:A=0.24m φ = 0 结束 返回
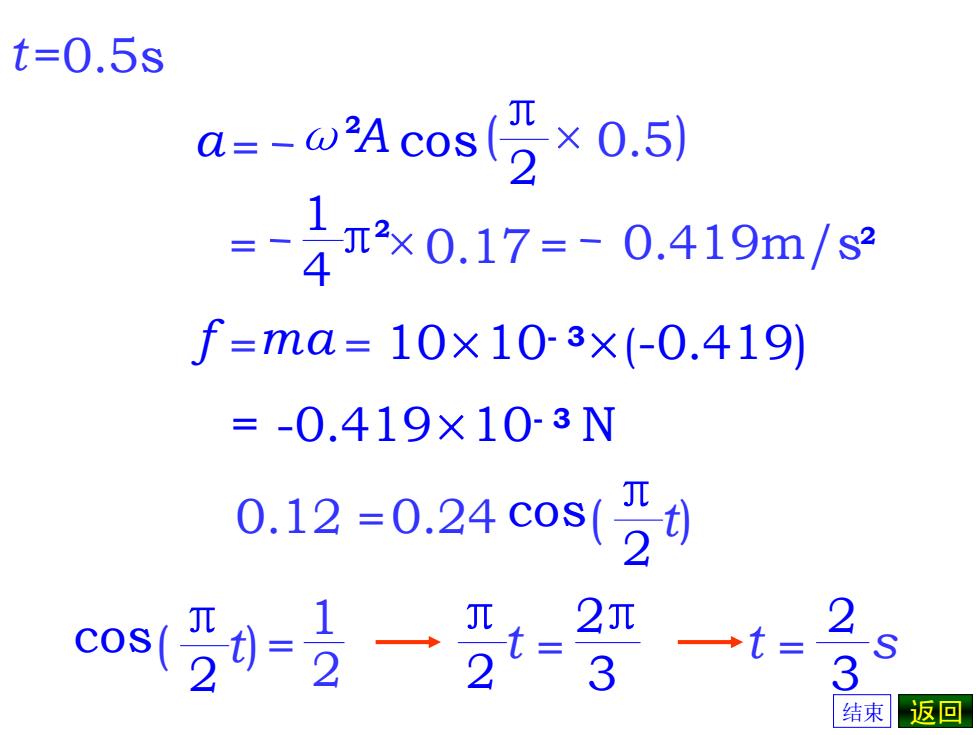
t=0.5s a=-wAcos(2×0.5) -4 r2×0.17=-0.419m/s f=ma=10×103×(-0.419) =-0.419×103N 0.12=0.24cos(2利 2元 2 →t= S 3 3 结束返回
f =ma 2 a= ω A cos (π × 0.5) 2 = × 0.17 1 4π2 = 0.419m/s2 = 10×10- 3×(-0.419) = -0.419×10- 3 N t=0.5s 0.12 =0.24 cos( ) 2 πt = 1 cos( ) 2 πt 2 = 2 πt 3 2π t = 3 2 s 结束 返回

U-Asin(到=-×0.24xsin Jπ 3 =-0.326m/s 2m2=1 E水- ×10×103×0.326)2 =5.31×104J kx2=0 其mw2x2 2×10×103x(22×0.12)2 =1.77×104U Ek=Ek+Ep=7.08×104J 结束返回
=-0.326m/s v= ωA sin ( ) 2 πt = ×0.24× 3 π 2 π sin 1 2 Ek mv2 = = ×10×10-3×(0.326)2 1 2 =5.31×10- 4 J 1 2 EP kx 2 = 1 2 m 2 = ω x 2 = ×10×10-3× 1 2 ×(0.12) ( ) 2 2 π 2 =1.77×10- 4 J Ek =Ek +Ep =7.08×10- 4 J 结束 返回