
结构理论 这里,由悬索CD段的平衡条件(见图1.56b),则有 -背 (j) 将式(j)代入式(),然后积分得 s=simh o 90 H (k 再由悬索CD段的平衡条件,有 S=√+(9os) (1) 将式(k)代入式(1),得到 S=Heosh o H 利用式(1.5),最后变为 S=H+9oy (m) 由此又再次看到在绳索的最低点C处拉力S最小,大小与H相等,并且随着向两端方向逐 渐增大,拉力在最高支座处有最大值。 利用式(m),可得到在A点和B点处的拉力,各自表示为 S=H+of,Sa=H+qof (n) 为了确定H的值,对AC、BC段连续应用式(1.5),得到 -{ewh智-小方={ah曾+ (0) 或者写成 (p) 将上面最后两个式子相加,并有a+b=l,可得到 分=acs2+hl小+ecoh((4+ (q) 在大多数实际问题中,跨度1、挠度∫、和悬索单位长度的重量9。都是已知的。因此 从式(q)中便可以得到最小拉力H,这样,先前所定义的悬索的任何量均能轻易地用H来计 算了。 习题 1.悬索如图1.57所示,承受垂直的总载荷为Q= 100000lbf,该栽荷是沿水平跨度1的均布栽荷。当1= 100,∫,=12n,h=10f时,确定悬索的最大拉力。 2.悬素如图1.57所示,承受垂直的总栽荷为Q= 100000lbf,该栽荷是沿水平跨度1的均布栽荷。如果 悬索最大的允许拉力为120000lbf,问当1=100f,h= 10时,悬索的跨度应当为多少? 3.长100的柔索,每英尺长度的重量为5b,在两等高 图1.57
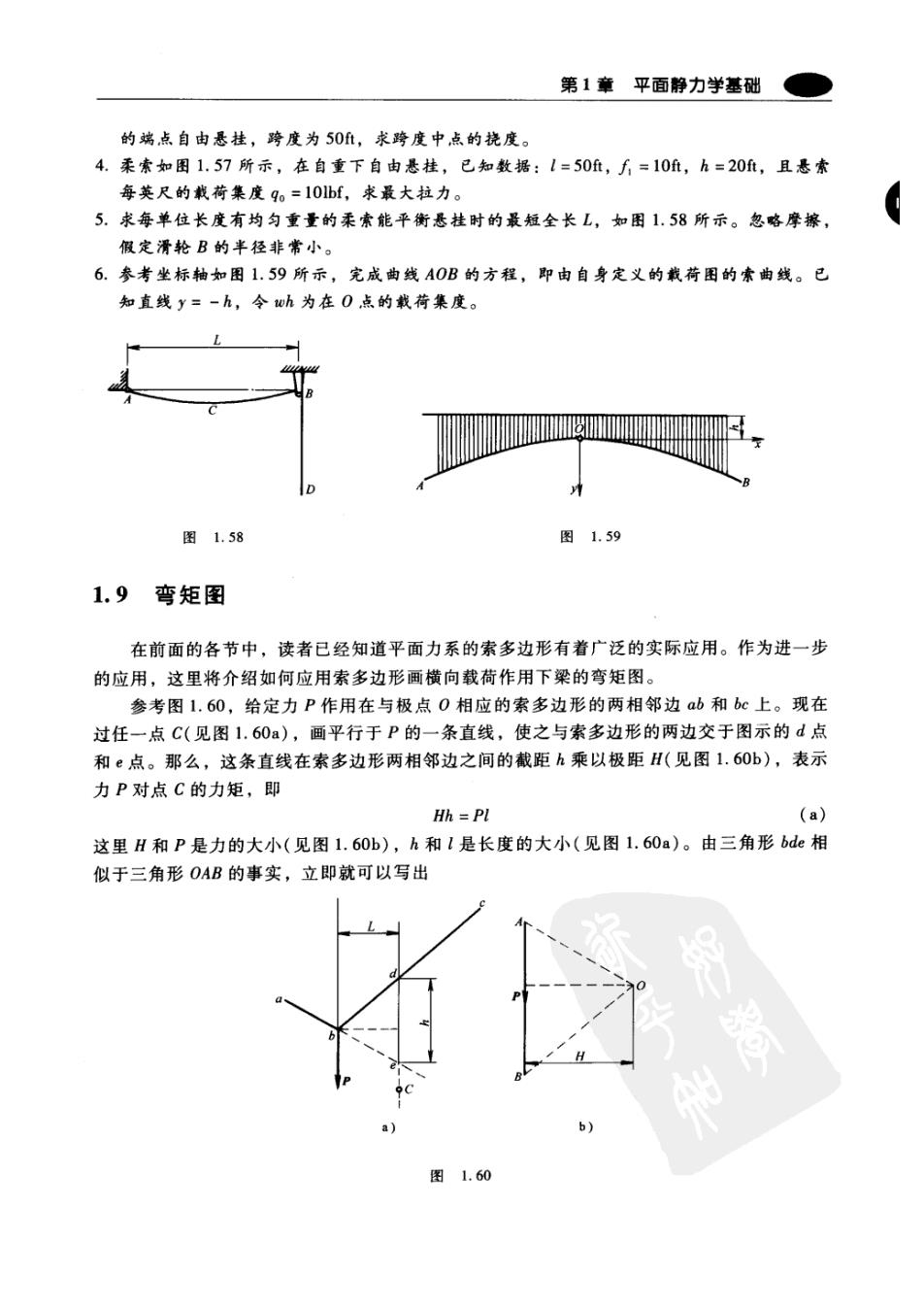
第1章平面静力学基础 的端点自由悬挂,跨度为50,求跨度中点的挠度。 4.柔索如图1.57所示,在自重下自由悬挂,已知数据:l=50丘,f=10,h=20t,且悬索 每英尺的栽荷集度9o=10lbf,求最大拉力。 5.求每单位长度有均匀重量的柔索能平衡悬挂时的最短全长L,如图1.58所示。忽略摩擦, 假定滑轮B的半径非常小。 6.参考坐标轴如图1.59所示,完成曲线A0B的方程,即由自身定义的戴荷图的索曲线。已 知直线y=-h,令wh为在O点的戴荷集度。 图1.58 图1.59 1.9 弯矩图 在前面的各节中,读者已经知道平面力系的索多边形有着广泛的实际应用。作为进一步 的应用,这里将介绍如何应用索多边形画横向载荷作用下梁的弯矩图。 参考图1.60,给定力P作用在与极点O相应的索多边形的两相邻边ab和bc上。现在 过任一点C(见图1.60a),画平行于P的一条直线,使之与索多边形的两边交于图示的d点 和e点。那么,这条直线在索多边形两相邻边之间的截距h乘以极距H(见图1.60b),表示 力P对点C的力矩,即 Hh=Pl (a) 这里H和P是力的大小(见图1.60b),h和l是长度的大小(见图1.60a)。由三角形bde相 似于三角形OAB的事实,立即就可以写出 周 a) b) 图1.60

结构理论 L:h=H:P 这个方程与式(a)等价。 上面的结论也可以应用于更普遍的例子中,图1.61所示的同一平面内的平行力系P,、 P2、…就是更普遍的例子。例如,假定用一般的方法已经建立了相应于极点0的索多边形 abedef。现在过任意矩心C,画已知力作用线的平行线。然后,这条直线在索多边形两相邻 边之间的截距乘以极距,表示包括索多边形这两边上的力对C点力矩的代数和。因此,要 得到所有力对C点力矩的代数和,则取截距FG乘以极距H即可。还有,要获得力P,、P2对 C点的力矩和,可用GL乘以H;对于P4对C点的力矩用FJ×H等等。力矩的正号或负号 对应于截距在两线交点的右边或左边。这个结论可直接由式()得到,因为索多边形任意两 边的交点决定了这两条边之间的所有力的合力作用线,合力矩总等于所有力之矩的代数和。 图1.61 现在,参考图1.62,再次考虑平行力系P,、P2、P,和P。,可知abedef是相应于极点O 的索多边形。如果在图示素多边形的第一边aa'与其余边上画平行于力的作用线来构造截 距,就可得到力矩图。图上任意一点的纵坐标乘以极距H表示纵坐标左侧的力对于坐标上 任意一点的力矩的代数和。参照图1.61的讨论,可直接得出此结论。现在,如果梁受横向 载荷作用,并且知道所有力对于任一点的一侧力矩的代数和是一个特定值,就可以把它定义 为梁上这一点的弯矩。因此,图1.62所示就表示为在B端固定,在力P,、P2、P,和P。作 用下的悬臂梁AB的弯矩图。 图1.62
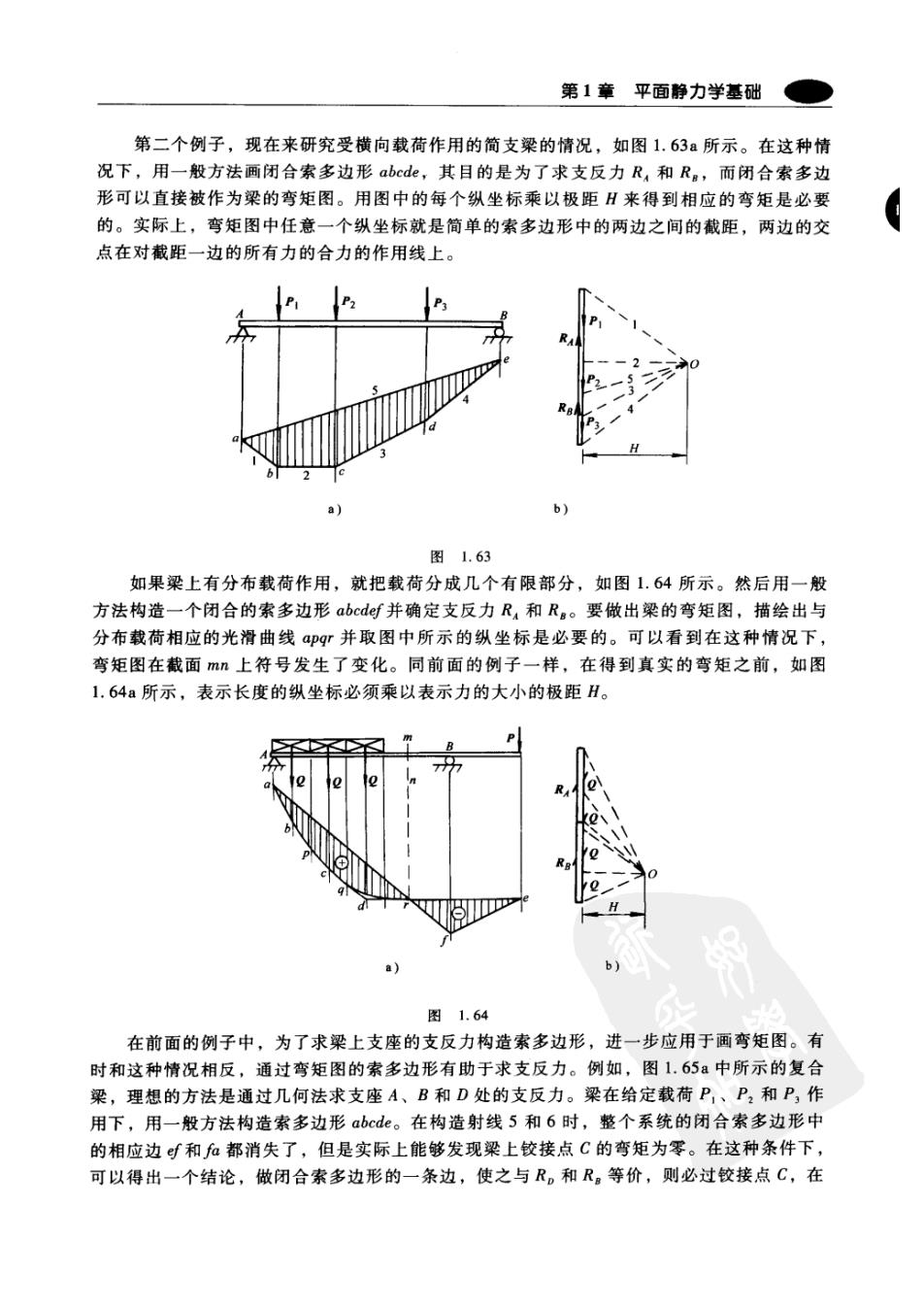
第1章平面静力学基础 第二个例子,现在来研究受横向载荷作用的简支梁的情况,如图1.63a所示。在这种情 况下,用一般方法画闭合索多边形abede,其目的是为了求支反力R,和R。,而闭合索多边 形可以直接被作为梁的弯矩图。用图中的每个纵坐标乘以极距H来得到相应的弯矩是必要 的。实际上,弯矩图中任意一个纵坐标就是简单的索多边形中的两边之间的截距,两边的交 点在对截距一边的所有力的合力的作用线上。 a)】 b) 图1.63 如果梁上有分布载荷作用,就把载荷分成几个有限部分,如图1.64所示。然后用一般 方法构造一个闭合的索多边形abedef并确定支反力R4和R。要做出梁的弯矩图,描绘出与 分布载荷相应的光滑曲线a即gr并取图中所示的纵坐标是必要的。可以看到在这种情况下, 弯矩图在截面m上符号发生了变化。同前面的例子一样,在得到真实的弯矩之前,如图 1.64a所示,表示长度的纵坐标必须乘以表示力的大小的极距H。 a) 图1.64 在前面的例子中,为了求梁上支座的支反力构造索多边形,进一步应用于画弯矩图。有 时和这种情况相反,通过弯矩图的索多边形有助于求支反力。例如,图1.65a中所示的复合 梁,理想的方法是通过几何法求支座A、B和D处的支反力。梁在给定载荷P,、P,和P,作 用下,用一般方法构造索多边形abcd。在构造射线5和6时,整个系统的闭合索多边形中 的相应边f和fa都消失了,但是实际上能够发现梁上铰接点C的弯矩为零。在这种条件下, 可以得出一个结论,做闭合索多边形的一条边,使之与R。和R。等价,则必过较接点C,在
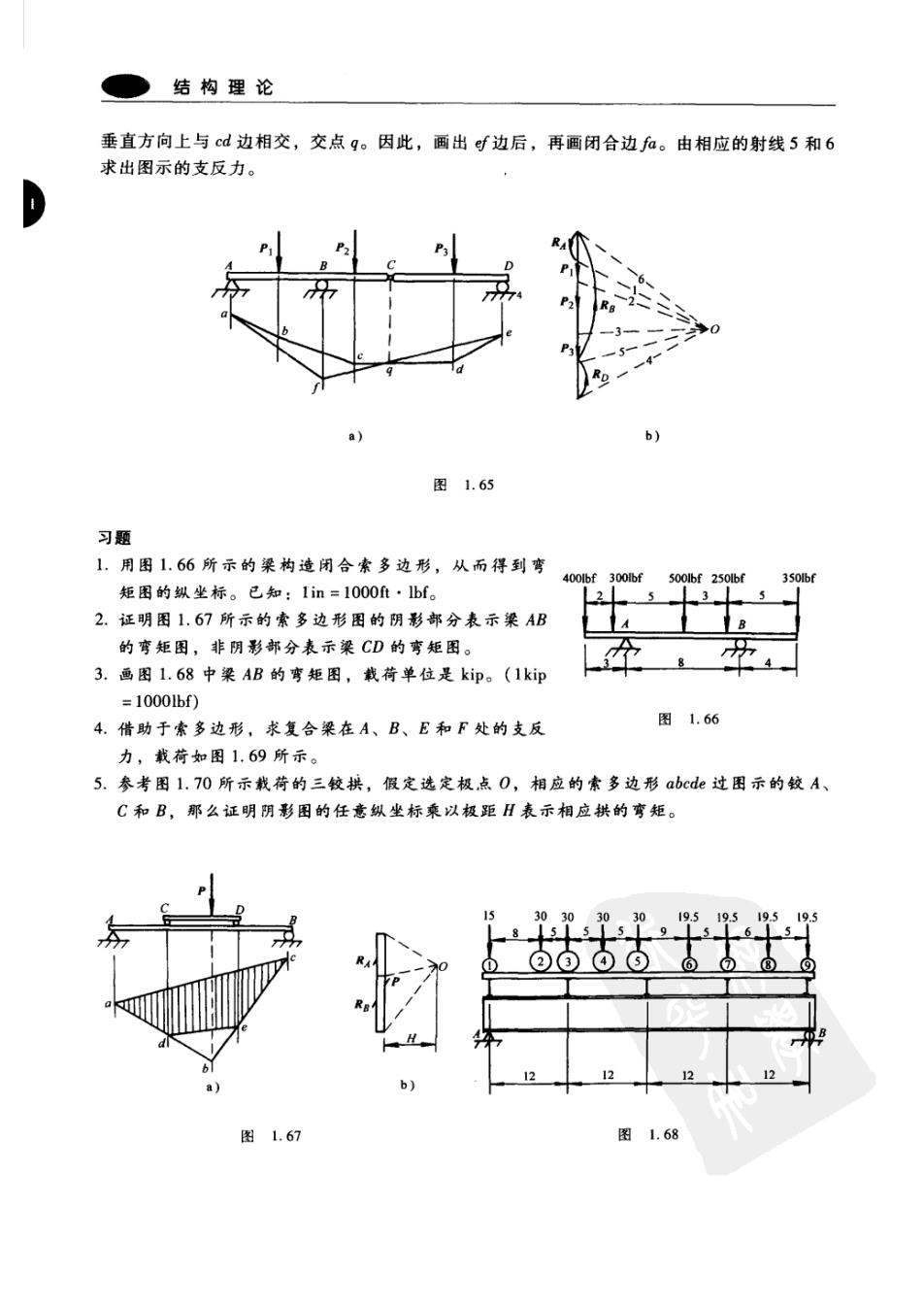
结构理论 垂直方向上与cd边相交,交点q。因此,画出时边后,再画闭合边fa。由相应的射线5和6 求出图示的支反力。 图1.65 习题 1.用图1.66所示的梁构造闭合索多边形,从而得到弯 400Ibf 300lbf so0lbf 250lbf 3s0lbf 矩图的纵坐标。已知:1in=l000f·bf。 2 3 2.证明图1,67所示的索多边形图的阴影部分表示梁AB 的弯矩图,非阴影部分表示梁CD的弯矩图。 3.画图1.68中梁AB的弯矩图,载荷单位是kip。(1kip =1000lbf) 4.借助于索多边形,求复合梁在A、B、E和F处的支反 图1.66 力,载荷如图1,69所示。 5.参考图1.70所示载荷的三较拱,假定选定极点0,相应的索多边形abcde过图示的较A、 C和B,那么证明阴影图的任意纵坐标乘以极距H表示相应拱的弯矩。 3030303019.519.519.519.5 8 155 5 12 2 12 12 a) b】 图1.67 图1.68