
第1章平面静力学基础 矩,与相应梯形的静矩相同。因此,下面所求的合力由载荷图的总面积表示,力作用线通过 载荷图的形心。 我们已经知道,任何共面力系的索多边形可以被看做是在给定力系作用下,两端固定的 绳索平衡的可能构型。对于在平面内连续地均布载荷的情况,如上面讨论的,相应的绳索平 衡的构型变成一个平滑的曲线,称作索曲线。实际上,这条曲线就表示为在自重下的柔索 链,它两端固定、其他部分在重力场中没有支座。这种特殊的曲线叫做悬链线。 让MmnW(见图1.52a)表示所给的平面内垂 直分布载荷的载荷图。为构造一个相应的索曲 线,首先将载荷图分成足够小的许多部分,因为 足够小,所以不会有很大的误差。并且,每一个 小部分都可以看作一个小的梯形。然后,每个梯 形都表示成一个垂直载荷,载荷的大小等于梯形 的面积,且作用线过形心。于是,可以将连续的 分布载荷替换为一些垂直的力P、P2、…等,并 且将这些力用通常的方法构造一个索多边形abc def。然后,可记下一条与索多边形各边相切的光 滑曲线,切点为g、h、i、j和k,这条曲线就是 a 所求的索曲线。 图1.52 在前面的讨论中,在每个索曲线(见图 1.52a)与相应的载荷图(见图1.52b)之间,存在以下关系: 1)每条索曲线的切线,在载荷图中都有一条相应的平行线,并且平行线的长度描述了 曲线上切点的张力大小。 2)载荷图中最短的直线,叫做极距H,表示索曲线顶点的张力。同样地,也表示其他 点的张力的水平投影。 3)索曲线上的任意两点,射线平行于相应被载重线AE截断的切线,是总载荷的一部 分,作用在两点之间。 下面举个例子来应用前面讨论的结果。现考虑一个对称的两端铰接的拱ACB,它受到一 个填土载荷的作用,如图1.53a所示。在这种情况下,对于载荷图AA'B'B,拱轴线是比较 理想的索曲线形式。如果这样,这个拱只受纯压力,没有弯矩。由于载荷图由拱轴线的形 状决定,因此,反过来,拱轴线的正确形状也受载荷图的影响。很显然,用几何方法来解决 这个问题必须作试验和误差分析。 我们开始就注意到,由于结构对称,拱肋的左半部分AC与右半部分BC形状相同,因 此只需要考虑拱肋的一半。如果沿拱肋的跨度作用一个均布载荷,拱肋的轴线的正确形状是 一个抛物线。所以采用AA'C'C(见图1.53b)作为轨迹载荷图是很方便的,且点A、D、E、 F、C在抛物线和垂直轴线上,C为顶点。 假定填土重100bf/,考虑垂直于平面图形的单位宽度的拱条。载荷可被表示为载荷 ⊙在本章讨论中,忽略了轴向压力引起的拱的缩短

结构理论 图的四个梯形,且载荷与这几个梯形的面积成比例。实际的数值标在每个梯形的顶部。这些 载荷P,、·、P4的作用线经过相对应的梯形面积的形心。选择任意点O,由这些力建立多 边形(见图1.53g),用一般的方法可以建立一个索多边形abedef(见图1.53c),并且应注意 所得到的力P,、、P,的合力的作用线由索多边形的第一条边和最后一条边的交点g决定。 很明显,受同样载荷的任何一个索多边形的第一条边和最后一条边必定相交于合力作用线。 所以我们能够得到一个索曲线,水平相切于C点且过A点,现在可以画相应的索多边形的 第一条边ag和最后一条边(见图1.53d),从而决定极点0,(见图1.53g)。有了这个极点, 可以画索多边形剩余的边bc、cd、de。与索多边形相切的曲线(没有画出),切点为A、D、 E、F、C,是理想索曲线的第一次近似。比较由虚线画出的曲线abedef(见图1.53b),与假 定的抛物线ADEFC,可以发现相当大的差异,这就需要做第二次近似。 为了作第二次近似,可用图1.53d中的A4'CC作为载荷图,如前所述,得到如图所示 的力P,、…、P。每个力的大小,与所对应的梯形的面积成比例,并标在每个梯形的顶部。 选择任意极点O',建立这些力的力多边形(见图1.53h),并画索多边形a'b'c'd'e'P(见图 D D' 13200 520 b) c) 0 12540 1260 4600 3460 比例:1"=200001b 01 比例:1”=20 图1.53

第1章平面静力学基础 1.53e)。索多边形的第一条边和最后一条边的交点g'决定载荷P、…、P4的合力作用线。 那么,如前所述,确定相应的过A点和水平方向的C点的索多边形的极点O'(见图1.53h)。 这个索多边形a'b'c'd'ef(见图1.53f)与abedef(见图1.53d)非常接近,由此可以认为得到的 曲线ADEFC(见图1.53)是所求的索曲线。可以注意到一个很有意思的问题,在特殊情况 下,获得的曲线与圆拱的曲线并没有很大区别。 1.8柔性悬索 在工程结构中,有时会遇到受垂直的分布载荷作用,两端支撑的悬素或链结构。当然, 假定索链的平衡形状是受约束索链的索曲线。为了解决这类问题,要得到索链的平衡形状, 用解析法比几何法更有效。 对此,参照图1.54a,图中MmnN代表垂直分布载荷,abcd是一条与极点O相应的索曲 线,如图1.54b所示。在这条索曲线上,选择两个相邻的点b和c,其相应坐标分别定义为 x和x+dx,与之相对应的斜率可用下列各式表达 和+( a 图1.54 这样,由先前各节所讨论过的关系可以得到 dy (a) dx tanBOE BE ds tnCOB- CE (b) OE 从式(b)中将式(a)减去,可得到 H 进而简化得到 g (1.3) 这个方程为对应于任意极距H的索曲线族的微分方程。对于任何特殊分布载荷9,相应的曲 线族可通过这个微分方程的积分得到。下面将进一步详细讨论两种特殊情况下的分布载荷。 沿跨度方向的均布载荷参照图1.55a,柔索ACB,在A点和B点受到支撑,一垂直载

结构理论 荷作用其上(未表示),相对于水平跨度!的载荷集度为9。将曲线上的最低点C定为坐标 原点,建立直角坐标轴x和y,如图1.55a所示。∫和方分别为支座A和B在y方向上的坐 标,a和b是x方向上的坐标。令q=q=常数,解微分方程(1.3)得 =90x2 y=2H (1.4) 可见,悬索的平衡曲线为在垂直轴上的抛物线。 a)】 图1.55 从悬索任意一段CD的平衡条件,可以得到D点的拉力S S=√m+(gx)7 (c) 这表明在悬索的最低点C处拉力最小,大小和H相等。随着向两端方向逐渐增大,拉力在 最高支座处有最大值。 对于悬索端点A和B处,各自的拉力由式(c)得 S4=√m+g6a Sa=√m+g68 (d) 为了确定a、b的距离,先确定A点和B点相对于最低点C的位置,然后对AC段、BC 段连续应用式(1.4),并注意到当x=-a时,y=∫,当x=b时,y=。于是可得到 方=器6-路 (e) 将表达式的第二式减第一式,利用,-f=h可得到 2hH=go(b2-a2) 然后,又因为a+b=l,则有 1 hH a= (f) 注意到,当h=0时,也就是说,当两个支撑点在同一水平面上时,有a=b: 2。 将上述表达式中的b代入式(e)中的第二式,便可得到下面计算H的方程式 H装6会同 (g) 在式(g)中,减号用于抛物线顶点在支座之间的任何情况;反之,加号用于顶点在两支座同 侧时,如图1.55所示双点划线AB。在特殊情况下,当两个支座位于同一水平高度时,即
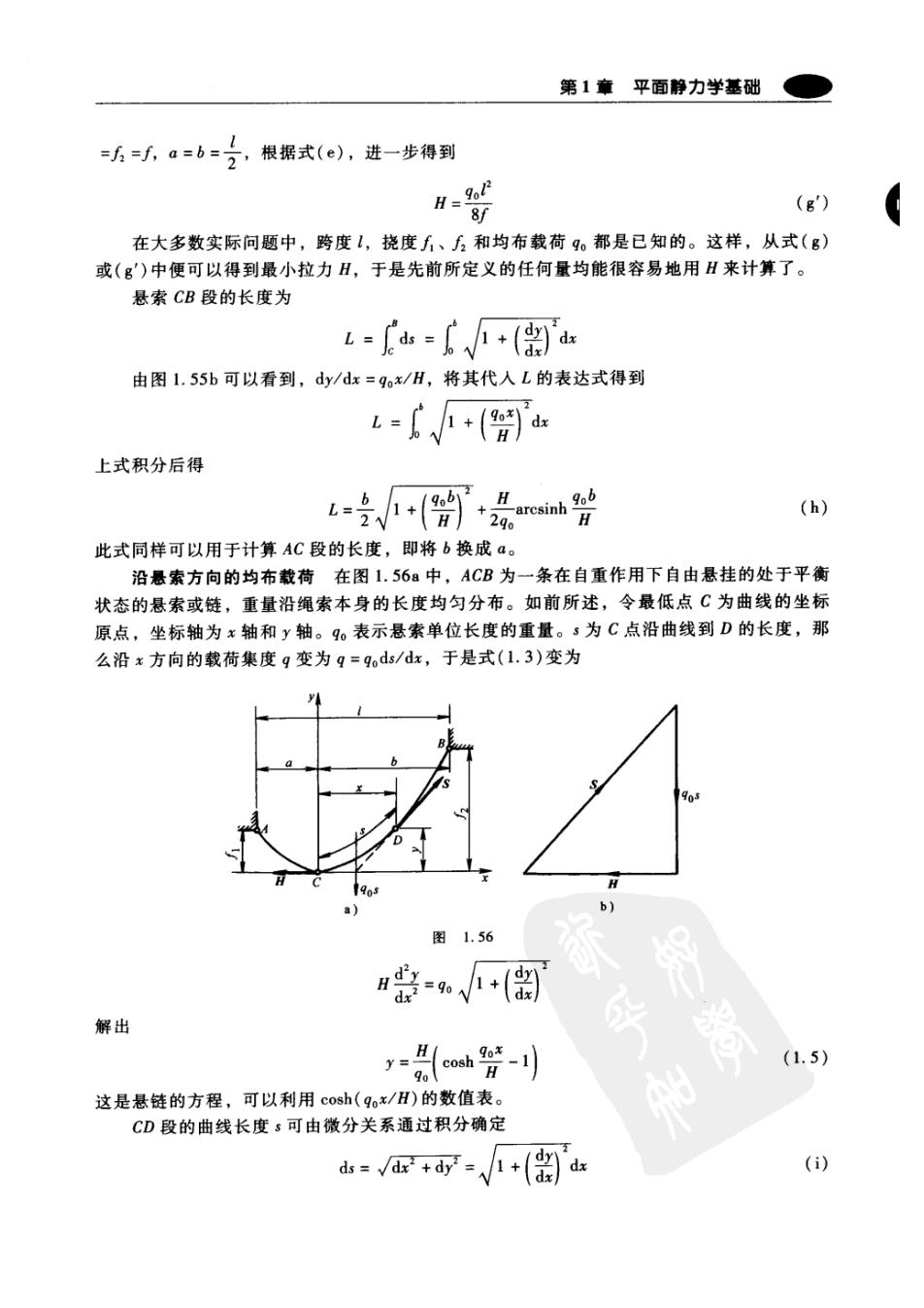
第1章平面静力学基础 =方=a=6=分,根据式(e),进一步得到 Hs9%2 8f (g) 在大多数实际问题中,跨度1,挠度f、和均布载荷9o都是已知的。这样,从式(g) 或(g)中便可以得到最小拉力H,于是先前所定义的任何量均能很容易地用H来计算了。 悬索CB段的长度为 L=ds=+(' 由图1.55b可以看到,dy/dx=gox/H,将其代人L的表达式得到 L=V+( 上式积分后得 (h) 此式同样可以用于计算AC段的长度,即将b换成a。 沿悬索方向的均布载荷在图1.56a中,ACB为一条在自重作用下自由悬挂的处于平衡 状态的悬索或链,重量沿绳索本身的长度均匀分布。如前所述,令最低点C为曲线的坐标 原点,坐标轴为x轴和y轴。9。表示悬索单位长度的重量。s为C点沿曲线到D的长度,那 么沿x方向的载荷集度q变为q=9ods/dx,于是式(1.3)变为 图1.56 =+ 解出 {oh- (1.5) 这是悬链的方程,可以利用cosh(qox/H)的数值表。 CD段的曲线长度s可由微分关系通过积分确定 的 d山=+时=√+(d (i)