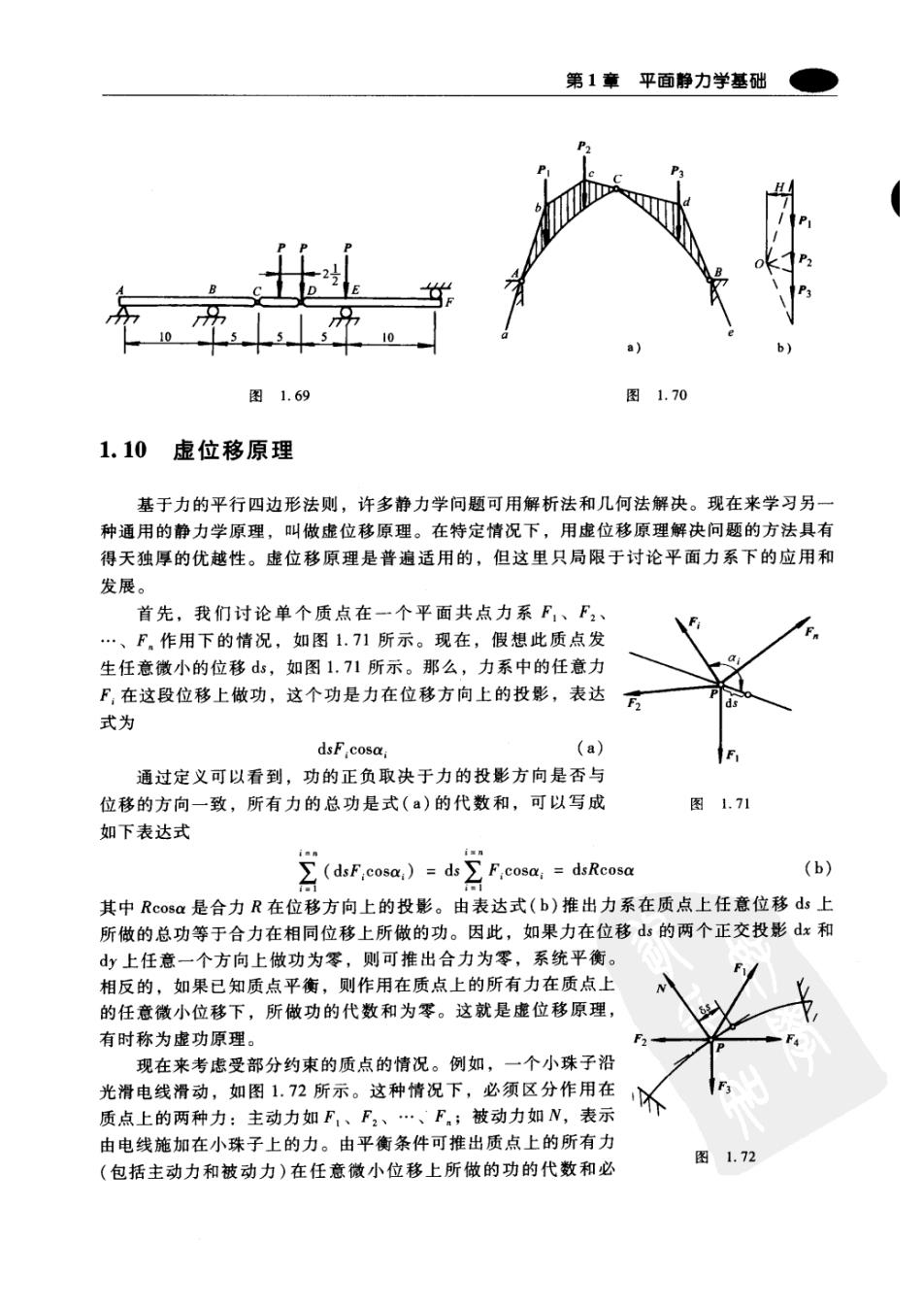
第1章平面静力学基础 a) 图1.69 图1.70 1.10 虚位移原理 基于力的平行四边形法则,许多静力学问题可用解析法和几何法解决。现在来学习另一 种通用的静力学原理,叫做虚位移原理。在特定情况下,用虚位移原理解决问题的方法具有 得天独厚的优越性。虚位移原理是普遍适用的,但这里只局限于讨论平面力系下的应用和 发展。 首先,我们讨论单个质点在一个平面共点力系F,、F2、 …、F。作用下的情况,如图1.71所示。现在,假想此质点发 生任意微小的位移ds,如图1,71所示。那么,力系中的任意力 F,在这段位移上做功,这个功是力在位移方向上的投影,表达 式为 dsF cosa; (a) 通过定义可以看到,功的正负取决于力的投影方向是否与 位移的方向一致,所有力的总功是式(a)的代数和,可以写成 图1.71 如下表达式 (dsF cosa,=dsFcosa,=dsR (b) 其中Rcosa是合力R在位移方向上的投影。由表达式(b)推出力系在质点上任意位移ds上 所做的总功等于合力在相同位移上所做的功。因此,如果力在位移ds的两个正交投影dx和 d山上任意一个方向上做功为零,则可推出合力为零,系统平衡。 相反的,如果已知质点平衡,则作用在质点上的所有力在质点上 的任意微小位移下,所做功的代数和为零。这就是虚位移原理, 有时称为虚功原理。 现在来考虑受部分约束的质点的情况。例如,一个小珠子沿 光滑电线滑动,如图1.72所示。这种情况下,必须区分作用在 质点上的两种力:主动力如F,、F2、…、F。;被动力如N,表示 由电线施加在小珠子上的力。由平衡条件可推出质点上的所有力 图1.72 (包括主动力和被动力)在任意微小位移上所做的功的代数和必

结构理论 为零。然而,假设限制了一个与约束相一致的位移,比如在电线上P点的切线方向上。那 么这个假想的质点的微小位移叫做虚位移,比如可能位移,虚位移用符号δs表示。如果电 线没有摩擦(理想约束),约束反力N垂直于虚位移δs,不做功。因此,所有力做的功只与 主动力作的功相一致。由此得到结论:对于任意理想约束下的质点,在任意虚位移上,主动 力所做功的代数和必为零。被动力根本不需要考虑。 最后来考虑最普遍的质点系的情况。虚位移原理被应 用到这样的系统中有特殊的意义。举一质点系的具体实例。 现考虑两个放在斜面上的滑块A和B,用一柔性的不可伸 长的绳子穿过滑轮,然后相连,如图1.73所示。如忽略滑 轮和斜面的摩擦,这种系统叫做理想系统。这里再次区分 主动力,如重力P和Q,被动力如N4、N。和S。然后,应 注意被动力有两种,作为整个系统的外力,比如N、NB; 图1.73 还有系统的内力,比如绳子施加在质点系上的拉力S。系统的虚位移,比如与约束相一致的 位置上的微小改变(包括内力和外力),将会得到图示每一个质点沿着支撑平面的假想位移 δ。因为绳子不能伸长,所以这些位移必然相等。那么,如果系统平衡,每一个质点平衡, 在这样的系统位移上所有力所做的功的代数和必然为零。但是,力N4、N。垂直于质点移动 方向的斜平面,不做功,不需要考虑。更进一步地说,力S大小相等,做功符号相反,相互 抵消,也可以不考虑。因此,对于任何一个平衡的理想质点系,在任意的虚位移上,所有主 动力做功的代数和为零。应用这个结论,可写出 -Psinaδx+Qsinβ8x=0 这里给出了系统的平衡条件 P=sing (c) 0 sina 要通过普通的平衡方程得到上述结果,可将每一个质点分开考虑,写出 Psina +S=0 Qsinβ-S=0 然后,消掉这两个方程中的S,可得到条件式(c)。对更复杂的几个质点系来说,后一 种方法需要同时写出许多平衡方程,将解决问题的过程变得非常复杂。这种情况下,虚位移 原理常常证明是更为实用的。 虚位移原理同样适用于任何理想连接的刚体系。例如,考虑如图1.74所示的杆系。为 了找到P和Q之间的平衡关系,应注意到系统的虚位移可 以定义为水平杆的一个微小转角δ8。重物P和Q的重心的 相应位移与在平底盘上的位置无关,并且总是大小相等。 因此,根据虚位移原理,重物P和Q为达到平衡必相等。 有时应用虚位移原理也有利于寻求支反力。例如,如 02 图1.75a所示,考虑在载荷作用下的简支铰接梁系统。要找 到B点的支反力,用假想的垂直力R。代替约束,如图 1.75b所示。这样,可得到一个需要寻找P和R。满足平衡 关系的非刚性系统。系统的虚位移完全定义为图中标出的 图 1.74
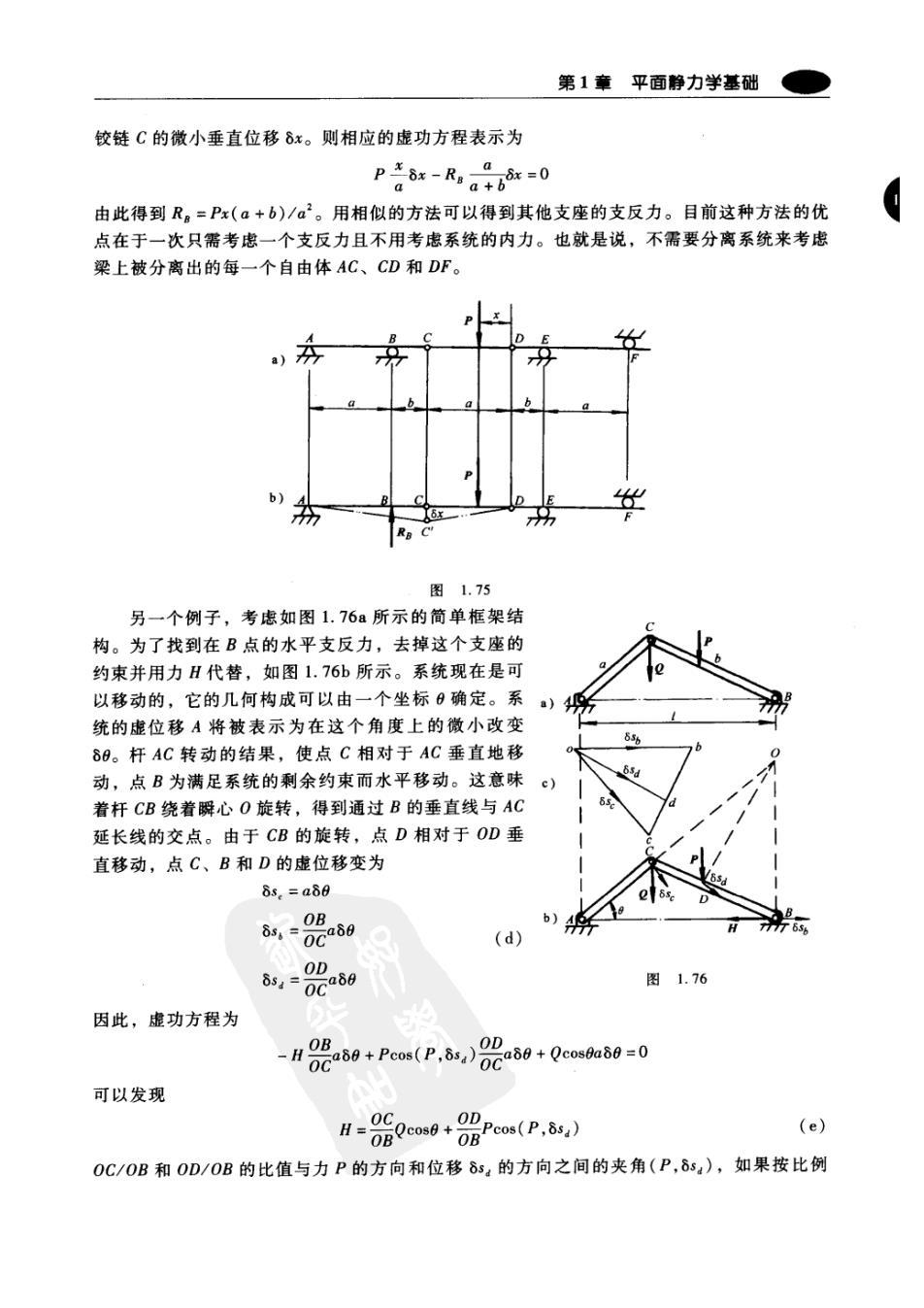
第1章平面静力学基础 铰链C的微小垂直位移δx。则相应的虚功方程表示为 Pδx-RB,a=0 a a +b 由此得到R。=Px(a+b)/a2。用相似的方法可以得到其他支座的支反力。目前这种方法的优 点在于一次只需考虑一个支反力且不用考虑系统的内力。也就是说,不需要分离系统来考虑 梁上被分离出的每一个自由体AC、CD和DF。 b) 图1.75 另一个例子,考虑如图1.76a所示的简单框架结 构。为了找到在B点的水平支反力,去掉这个支座的 约束并用力H代替,如图1.76b所示。系统现在是可 以移动的,它的几何构成可以由一个坐标6确定。系 统的虚位移A将被表示为在这个角度上的微小改变 65% 80。杆AC转动的结果,使点C相对于AC垂直地移 动,点B为满足系统的剩余约束而水平移动。这意味 65u c) 着杆CB绕着瞬心O旋转,得到通过B的垂直线与AC 6 延长线的交点。由于CB的旋转,点D相对于OD垂 直移动,点C、B和D的虚位移变为 8s.=a88 OB b) 8,-0Ca60 (d) OD δ54= OCa88 图1.76 因此,虚功方程为 H 60+Pcos(P,8,)8060+0eoe60=0 OB 可以发现 H=0GQcos0+ OD Pcos(P,8s4) (e) OB OB OC/OB和OD/OB的比值与力P的方向和位移δs:的方向之间的夹角(P,δs),如果按比例

结构理论 作图的话,可以从图中求出。 如果从极点O开始(见图1.76c),可建立矢量ob、od和oc,按一定比例分别得到位移 δs、8s:和8s。,这样得到的图obdc,几何上相似于图形OBDC,因为相应的边是互相垂直 的,且它们长度的比率不变。这两张图之间的关系适用于所有在一个平面内的单个刚体的位 移情况,obdc这样的图叫做位移图。借助于位移图,具有一个自由度的系统中的许多点的一 系列相应虚位移都可以容易地找到,然后就可以轻松地写出虚功方程了。 习题 1.参考图1.41所示的粱,用虚位移方法,求图示栽荷P作用下斜杆的拉力S2。 2.简支复合梁ACB,载荷如图1.77所示。用虚位移原理,求垂直杆1和杆2的轴力。 3.用虚功原理,计算图1.69所示复合粱的E点的支反力。 4.用虚位移原理,求图1.78所示载荷作用下,较接框架在支座A和B处引起的水平和铅垂 支反力。 5.如图1.35所示的半圆三较拱,建立虚位移图,并求图示载荷P作用下的水平推力H。 B 图1.77 图1.78 格是 阀

第2章 静定平面桁架 2.1简单桁架 平面桁架是最重要的结构形式之一。通常,由若干在同一平面内的直杆在端点处铰接而 成的刚性框架体系称为平面桁架。如图2.1所示的两个简单框架就属于平面桁架。图2.1a 中的矩形框架是由四根端点相互铰接的杆组成的。显然该结构不是刚性的,有可能变形成为 如图中双点划线所示的结构。这个结论同样适用于由多于四根杆组成的铰接多边形结构。另 一方面,如图2.1b所示,由三根在端点相互铰接的杆构成的三角形结构是几何不变体系, 也就是说,忽略杆在长度上的小变形,A、B和C三点铰接的相对位置不会改变。因此,这 种基本铰接三角形构成的刚性结构是桁架的最简单形式。 如图2.2a所示,由一个铰接三角形ABC开始,增加杆AD和BD,用销钉固定在D点,显 然,刚性三角形ABC和杆AD、杆BD也排列成三角形形式,于是就得到刚性框架ABCD。同理, 如图2.2b所示,在刚性结构ABCD部分增加杆DE和CE,铰接点为E,就得到刚性桁架ABCDE。 b) 图2.1 图2.2 由于上面讲到的过程可以无限地继续下去,可以推出:首先由一个三杆的基本铰接三角 形开始,然后每增加一个新结点,就要增加两根杆连接新结点,这样就形成了一个平面刚性 桁架。依据这样的原则组成的桁架称为简单桁架。如图2.3所示的桁架就是简单桁架,三 角形ABC作为基本单元,然后按照字母顺序,每增加一个结点增加两根杆,依次连接结点 D、E、F和G,就组成了一个简单桁架。 在图2.3b中,这个简单桁架和前述的规律有微小变化。这种情况不是从一个铰接三角 形开始,而是直接从一个刚性基础(比如说垂直的墙)开始,按照字母顺序建立桁架结点, 每次在原有系统上增加两根杆。图2.3b所示的这种简单桁架不同于图2.3a所示的情况,它