
第1章平面静力学基础 一个平面上的刚体,支座和载荷如图1.28a所示。在已知载荷作用下,支座反力为R,和 Rg。通常,通过考虑整体的平衡条件可以确定其反力。这就完全确定了作用于整体上的外 部力系。现在,假设用任意横截面mn将整体划分成J和K两个部分,如图1.28a所示。显 而易见,内部约束力必存在于分开的两个部分,并使这两部分结合在一起。当然,这样的内 力总是成对出现在整体的每一个点上,大小相等、方向相反,并且不会被考虑到整体平衡 上。鉴于此,取隔离体K作为一个自由体(见图1.28b),被移走的J部分的作用力可以通过 作用在自由体K上不同质点处的力来表示。这样,就引入了要求解的内力。 虽然作用在截面上的内力的实际分布可能是复杂的,但显而易见,作用于J外部的力系 必须是静平衡的,且总可以由作用在截面形心处的合力R和一力偶M共同表示。如图1.28c 所示,合力R可被依次分解成相互垂直的分力N、V。在截面mn上的这三个量N、V、M分 别被称为法向内力、切向内力和内力矩。如图1.28所示的方向通常被认为是正方向。通常, 它们的大小取决于选取截面的位置和方向,但是无论如何,在自由体K上,它们可以通过 三个平衡方程来确定。 图1.28 现在研究最简单却又是最重要的结构类型:受横向载荷作用的梁在不同截面处的内力。 这样的梁通常是等截面直梁,在对称平面上受约束和载荷作用。在这些条件下,用横截面垂 直于梁的轴线定义一般状态的内力一轴力、剪力和弯矩。例如,悬臂梁AB,所受载荷如 图1.29a所示,在距离自由端x处定义一个任意垂直截面mn,然后根据此截面右半部分自 由体的平衡,由式(1.2a)可得到 N,=+Psina V.=+Pcosa M.=-Pxcosa 从这些表达式看,轴力N,和剪力V,与梁上截面的位置无关,而弯矩M,与x的距离成 正比。梁上轴力、剪力和弯矩的变化可用图1.29c中的各个图表示出来,这些图相应地被称 为轴力图、剪力图和弯矩图。 第二个例子,考虑图1.30a所示的悬臂梁,沿梁的长度方向作用均布载荷。在这种情况 下,距离梁的自由端x处截面上的轴力、剪力和弯矩的表达式为 N,=0V.=+0x M.=-0x 2 相应的图形如图1.30b所示
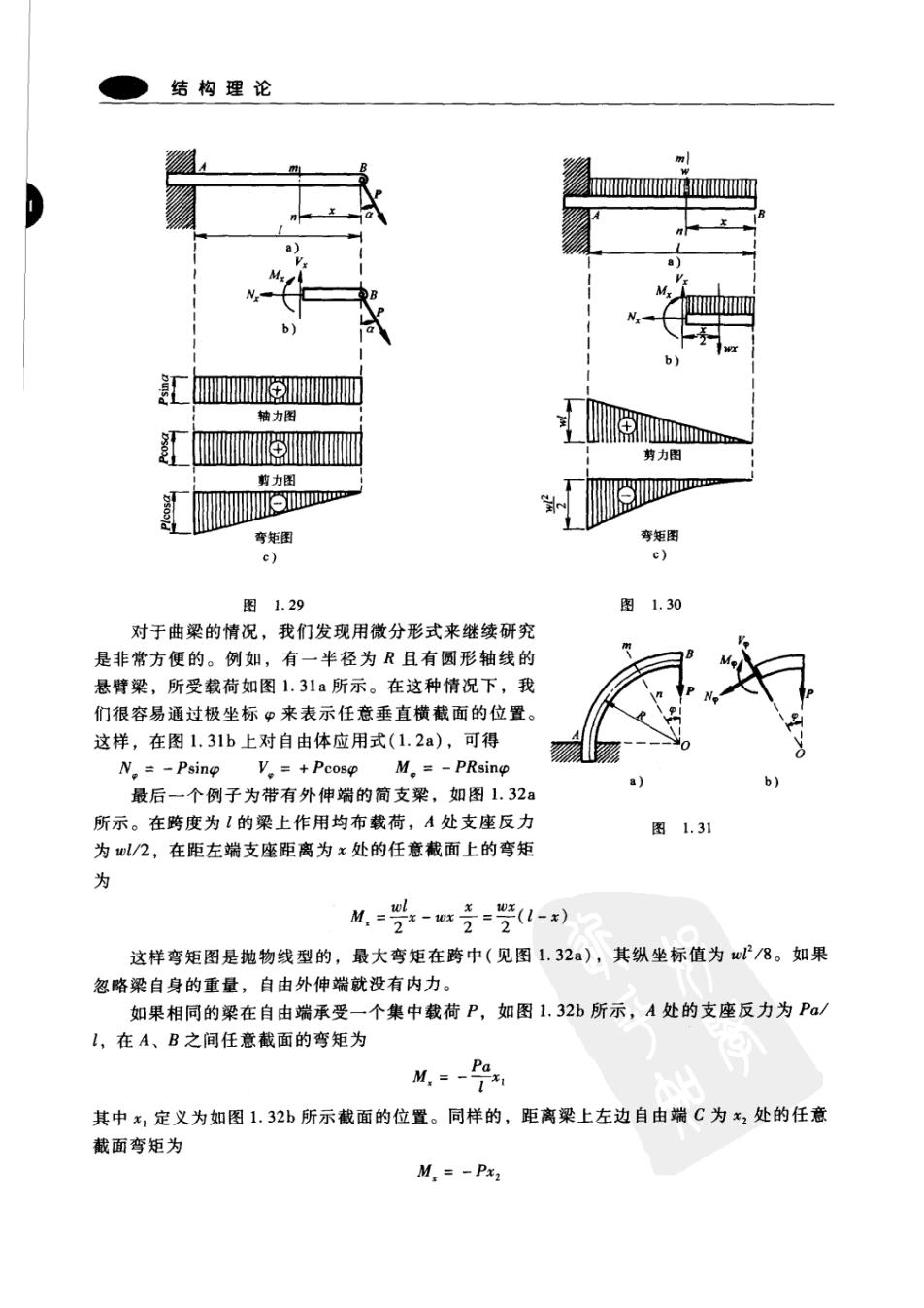
结构理论 KK M N b) 轴力图 smma 剪力图 剪力图 弯矩图 弯矩图 c) c) 图1.29 图1.30 对于曲梁的情况,我们发现用微分形式来继续研究 是非常方便的。例如,有一半径为R且有圆形轴线的 悬臂梁,所受载荷如图1.31a所示。在这种情况下,我 们很容易通过极坐标P来表示任意垂直横截面的位置。 这样,在图1.31b上对自由体应用式(1.2a),可得 N。=-Psing V。=+Pcoso M。=-PRsino b) 最后一个例子为带有外伸端的简支梁,如图1.32 所示。在跨度为1的梁上作用均布载荷,A处支座反力 图1.31 为wl/2,在距左端支座距离为x处的任意截面上的弯矩 为 M.-以 这样弯矩图是抛物线型的,最大弯矩在跨中(见图1.32a),其纵坐标值为wl/8。如果 忽略梁自身的重量,自由外伸端就没有内力。 如果相同的梁在自由端承受一个集中载荷P,如图1,32b所示,A处的支座反力为Pa/ 1,在A、B之间任意截面的弯矩为 M=- 其中x,定义为如图1.32b所示截面的位置。同样的,距离梁上左边自由端C为2处的任意 截面弯矩为 M.=-Px2

第1章平面静力学基础 mmmmmmmA mmmm P/I-(I+a) mEIII ST emIEBng a) b) c) 图1.32 这种情况下,弯矩图是由在B支座处有共同的最大纵坐标值为一Pa的两条直线所组成的。 如果梁同时承受均布载荷和集中载荷,可以简单地通过将图1.32a和图1.32b的弯 矩图叠加,得到相应的弯矩图,如图1.32c所示。同样的过程可用于建立剪力图和轴 力图。 习题 1.建立如国1.33所示的每一个悬臂梁的剪力图和弯矩图。 2.建立如图1.15~图1.17中每一个梁的轴力图、剪力图和弯矩图。 3.建立如图1.34所示的每一个简支梁的剪力图和弯矩图。 4.建立如图1.27所示结构中BC梁的轴力图、剪力图和弯矩图。 5.证明图1.35所示的垂直坐标表示三较拱在半圆拱相应点上的弯矩。三较拱受力如图1.35 所示。为了给出相应的弯矩,计算每一个坐标必须乘以的因子。 a a) StiI c) 图1.33 图 1.34 图1.35

结构理论 1.5索多边形 现在阐述一种解决共面力系的通用几何方法,这种方法比用分析方法来解决1.3节中讨 论的问题更有实用优势。首先,用一个只有两个力P和Q的简单例子来说明该方法,如图 1.36a所示。我们已经知道,力多边形(见图1.36b)的封闭边矢量AC给出了这两个力的合 力的大小和方向,但是力作用线的位置仍亟待解决。通常,这可由下面的步骤来完成。在图 1.36b中任意选一点0,叫做极点,然后用线1、2、3连接力多边形的顶点。这些线叫做射 线,就像图中其他线一样,称为自由矢量。例如,在三角形AOB内,方向如箭头所示,这 样可以认为力P是力1和2的合力。同理,力Q可以看作是力2和3的合力,方向如三角形 BOC内的箭头所示。现在,参照图1.36a,如果力P和Q分别被其两个分力代替,显然力P 和Q的作用不会改变。替代方法如下:首先,在力的作用平面上的任意点α,我们画平行于 射线AO的线ab。过ab与力P的作用线的交点b,画平行于射线B0的直线bc;接着,过bc 与力Q的作用线的交点c,画平行于射线C0的直线cd。用这种方法得到的多边形abcd就叫 做力P和Q的索多边形。这个索多边形的顶点都在已知力的作用线上,各边都平行于力多边 形的射线。现在假定在b点用力1和2代替力P,在c点用力2和3代替力Q,如图1.36a所 示。这样在b点和c点的四个力所组成的力系就代替了已知力系P和Q。由于沿bc方向的力2 是一对力,大小相等、方向相反,因此这对力从系统中消掉。这样只剩下力1和3,它们和已 知力P、Q作用相同。这些力的合力的大小和方向由1.36b图中的矢量AC给出。合力作用线上 的一点由沿着索多边形的起始边和终止边的力1和3的交点e来确定,如图1.36a所示。 图1.36 如果我们想象沿着索多边形的边ab、bc和cd,有一条无重的绳索,固定端在a和d,则 这条绳子在力P和Q的作用下平衡。在绳索的ab和bc段的张力大小等于力1和2的大小, 他们在结点b上的作用力和力P平衡,同理,在绳索的bc和cd段的张力与力Q平衡。建立 的索多边形abcd和满足已知力作用的绳子的平衡之间的关系解释了索多边形名字的来源。 上述讨论的几何构建的方法是非常通用的,该方法也可以应用到一些共面力问题上,如 图1.37a所示的P,、·、P5。首先应从建立力多边形ABCDEF开始。选任意一极点O,画 射线1、2、3、4、5、6,并在力的作用平面内建立平行于这些射线的线ab、bc、…、fg,这 样就得到了如图1.37所示的索多边形abcdefg。在这个多边形的每一个顶点上,每一个已知
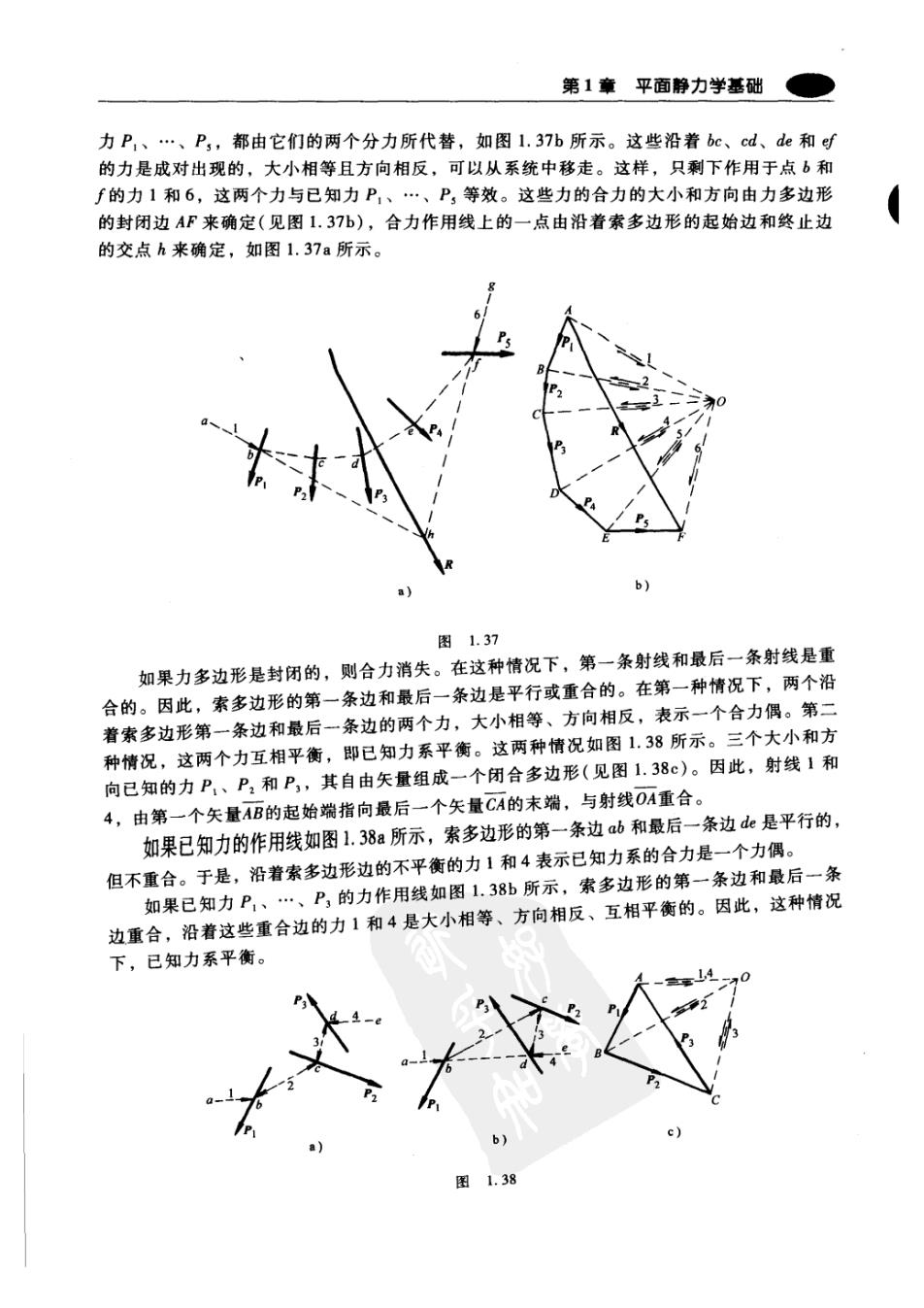
第1章平面静力学基础 力P,、·、P,都由它们的两个分力所代替,如图1.37b所示。这些沿着bc、cd、de和ef 的力是成对出现的,大小相等且方向相反,可以从系统中移走。这样,只剩下作用于点b和 f的力1和6,这两个力与已知力P,、…、P,等效。这些力的合力的大小和方向由力多边形 的封闭边AF来确定(见图1.37b),合力作用线上的一点由沿着索多边形的起始边和终止边 的交点h来确定,如图1.37a所示。 图1.37 如果力多边形是封闭的,则合力消失。在这种情况下,第一条射线和最后一条射线是重 合的。因此,索多边形的第一条边和最后一条边是平行或重合的。在第一种情况下,两个沿 着索多边形第一条边和最后一条边的两个力,大小相等、方向相反,表示一个合力偶。第二 种情况,这两个力互相平衡,即已知力系平衡。这两种情况如图1.38所示。三个大小和方 向已知的力P,、P2和P,,其自由矢量组成一个闭合多边形(见图1.38c)。因此,射线1和 4,由第一个矢量AB的起始端指向最后一个矢量CA的末端,与射线OA重合。 如果已知力的作用线如图l.38a所示,索多边形的第一条边ab和最后一条边de是平行的, 但不重合。于是,沿着索多边形边的不平衡的力1和4表示已知力系的合力是一个力偶。 如果已知力P1、…、P,的力作用线如图1.38b所示,索多边形的第一条边和最后一条 边重合,沿着这些重合边的力1和4是大小相等、方向相反、互相平衡的。因此,这种情况 下,已知力系平衡。 1.38