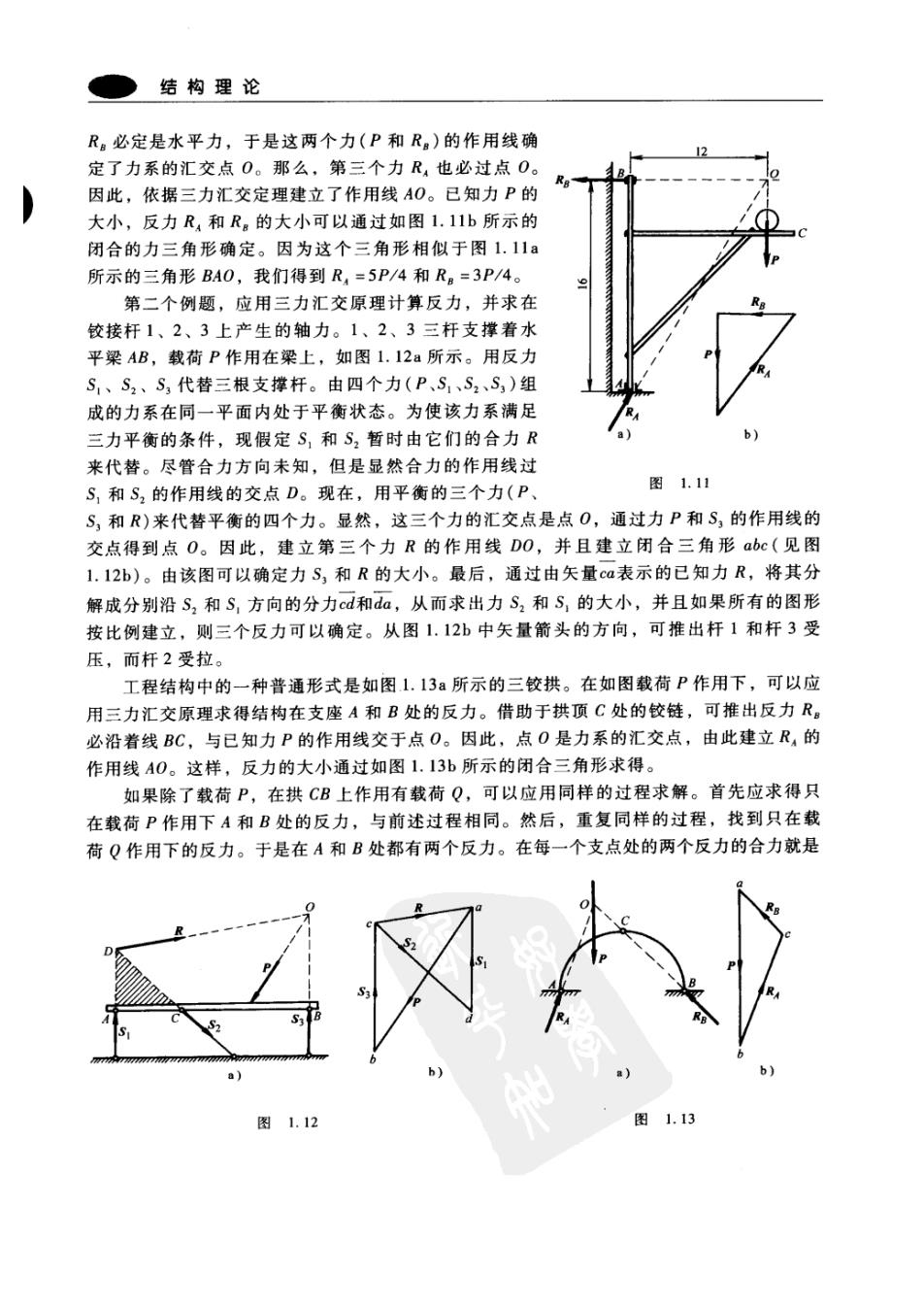
结构理论 R。必定是水平力,于是这两个力(P和R。)的作用线确 定了力系的汇交点O。那么,第三个力R4也必过点O。 R8- 因此,依据三力汇交定理建立了作用线AO。已知力P的 大小,反力R,和R。的大小可以通过如图1.11b所示的 闭合的力三角形确定。因为这个三角形相似于图1.11a 所示的三角形BA0,我们得到R,=5P/4和Rg=3P/4。 第二个例题,应用三力汇交原理计算反力,并求在 铰接杆1、2、3上产生的轴力。1、2、3三杆支撑着水 平梁AB,载荷P作用在梁上,如图1.12a所示。用反力 S,、S2、S,代替三根支撑杆。由四个力(P、S、S2、S)组 成的力系在同一平面内处于平衡状态。为使该力系满足 三力平衡的条件,现假定S,和S2暂时由它们的合力R 来代替。尽管合力方向未知,但是显然合力的作用线过 S,和S2的作用线的交点D。现在,用平衡的三个力(P、 图1.11 S,和R)来代替平衡的四个力。显然,这三个力的汇交点是点O,通过力P和S,的作用线的 交点得到点O。因此,建立第三个力R的作用线DO,并且建立闭合三角形abc(见图 1.12b)。由该图可以确定力S,和R的大小。最后,通过由矢量ca表示的已知力R,将其分 解成分别沿S,和S,方向的分力cd和da,从而求出力S2和S,的大小,并且如果所有的图形 按比例建立,则三个反力可以确定。从图1.12b中矢量箭头的方向,可推出杆1和杆3受 压,而杆2受拉。 工程结构中的一种普通形式是如图1.13a所示的三铰拱。在如图载荷P作用下,可以应 用三力汇交原理求得结构在支座A和B处的反力。借助于拱顶C处的铰链,可推出反力R。 必沿着线BC,与已知力P的作用线交于点O。因此,点O是力系的汇交点,由此建立R,的 作用线AO。这样,反力的大小通过如图1.13b所示的闭合三角形求得。 如果除了载荷P,在拱CB上作用有载荷Q,可以应用同样的过程求解。首先应求得只 在载荷P作用下A和B处的反力,与前述过程相同。然后,重复同样的过程,找到只在载 荷Q作用下的反力。于是在A和B处都有两个反力。在每一个支点处的两个反力的合力就是 图1.12 图1.13
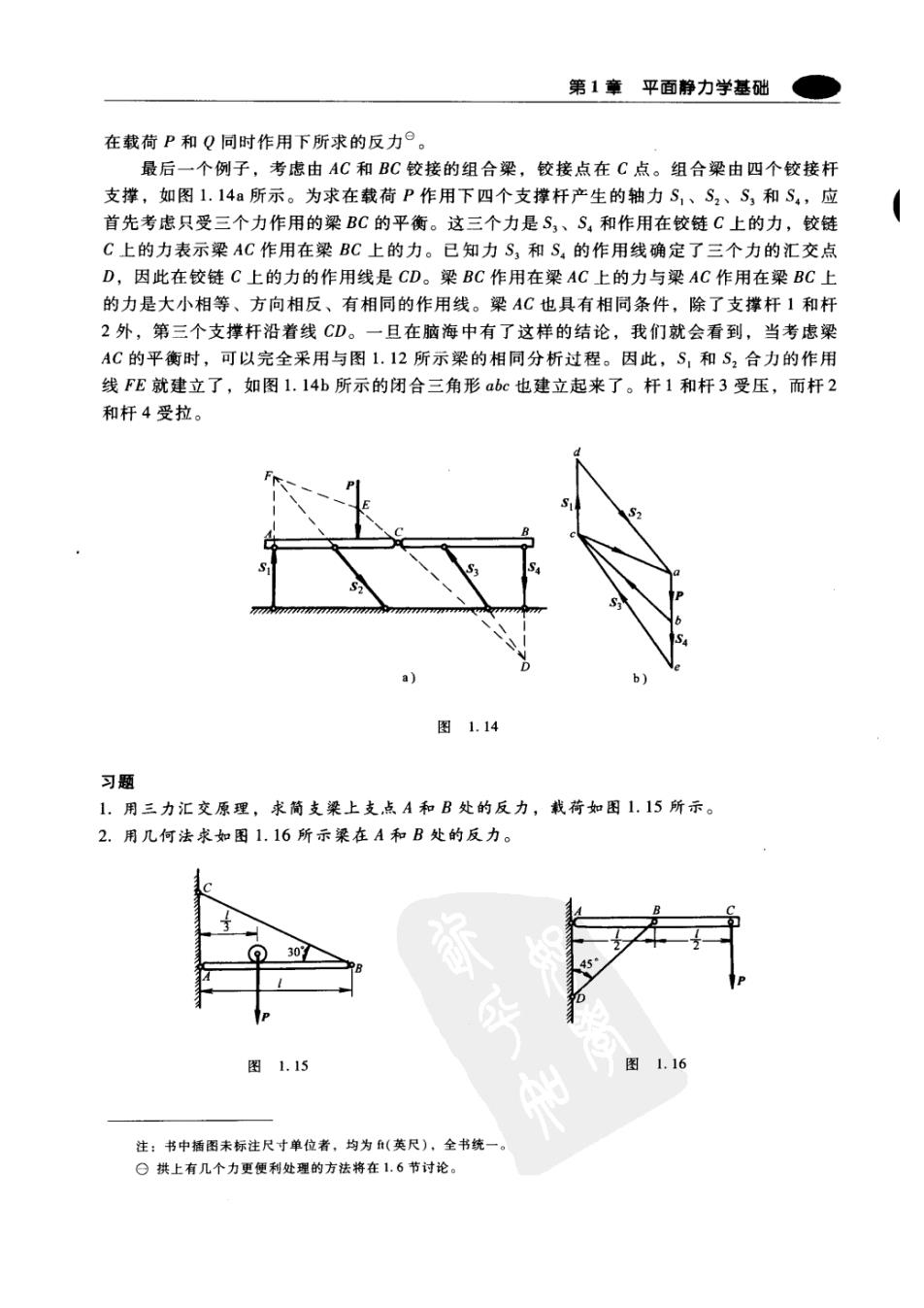
第1章平面静力学基础 在载荷P和Q同时作用下所求的反力°。 最后一个例子,考虑由AC和BC铰接的组合梁,铰接点在C点。组合梁由四个铰接杆 支撑,如图1.14a所示。为求在载荷P作用下四个支撑杆产生的轴力S,、S2、S,和S,应 首先考虑只受三个力作用的梁BC的平衡。这三个力是S,、S,和作用在铰链C上的力,铰链 C上的力表示梁AC作用在梁BC上的力。已知力S,和S4的作用线确定了三个力的汇交点 D,因此在铰链C上的力的作用线是CD。梁BC作用在梁AC上的力与梁AC作用在梁BC上 的力是大小相等、方向相反、有相同的作用线。梁AC也具有相同条件,除了支撑杆1和杆 2外,第三个支撑杆沿着线CD。一旦在脑海中有了这样的结论,我们就会看到,当考虑梁 AC的平衡时,可以完全采用与图1.12所示梁的相同分析过程。因此,S,和S2合力的作用 线FE就建立了,如图1.14b所示的闭合三角形abc也建立起来了。杆1和杆3受压,而杆2 和杆4受拉。 。 D a) b 图1.14 习题 1.用三力汇交原理,求简支梁上支点A和B处的反力,载荷如图1.15所示。 2.用几何法求如图1.16所示粱在A和B处的反力。 0 图1.15 图1.16 注:书中插图未标注尺寸单位者,均为(英尺),全书统一。 日拱上有几个力更便利处理的方法将在1.6节讨论

结构理论 3.用几何法求如图1.17所示梁在A和B处的反力。 4.重W的等截面直杆靠在水平地面A和垂直墙B上,绳子OD使杆不致倾倒,如图1.18所 示。忽略在支,点处的摩擦,用几何法求A和B处的反力以及绳子OD的拉力。 5.用几何法求组合结构在支点处的反力R4和Rg,载荷如图1.19所示。 (提示:B处的反力是水平力) D 5.4 图1.17 图1.18 图1.19 1.3平衡方程 一般来说,力的作用线不交于一点的共面力系可以合成为:①一个合力;②一个合力 偶;③达到平衡状态。 给定力系P,、P2、P,和P4,如图1.20b所示,这四个力的自由矢量组成一个非封闭的 力多边形,该力系最后合成为一个合力,合力的大小和方向由力多边形的封闭边AE表示, 如图1.20a所示。 图1.20 如果给定力系的自由矢量组成一个封闭的力多边形如图1.21b所示,则合力为零,但也 可能是一个力偶。在这种情况下,将力任意分解成两组P,、P2、P,与P,、P,、P。,最后得 到两个大小相等、方向相反的合力R,、R2,如图1.21b中的矢量AD和DA,任选力系中的几 个力都可以这样去分组。最后,如果合力的作用线如图1.21a所示,这两个大小相等方向相 反的合力组成一个合力偶。 特殊情况下,如果力的作用线R,与R2共线,如图1.21a所示,则合力偶为零,此力系
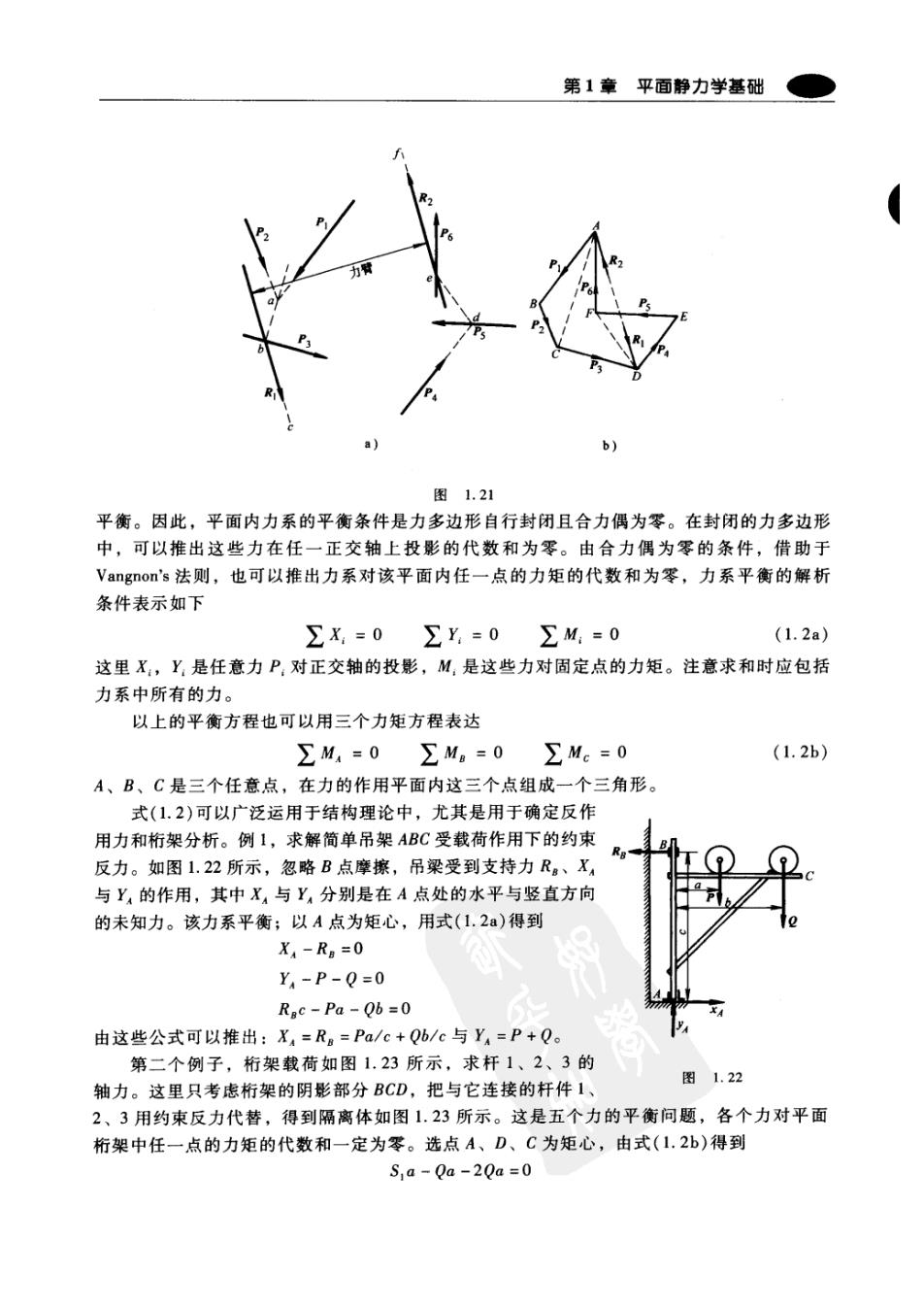
第1章平面静力学基础 a)】 b) 图1.21 平衡。因此,平面内力系的平衡条件是力多边形自行封闭且合力偶为零。在封闭的力多边形 中,可以推出这些力在任一正交轴上投影的代数和为零。由合力偶为零的条件,借助于 Vangnon's法则,也可以推出力系对该平面内任一点的力矩的代数和为零,力系平衡的解析 条件表示如下 ∑X=0∑y=0 ∑M:=0 (1.2a) 这里X:,Y,是任意力P:对正交轴的投影,M:是这些力对固定点的力矩。注意求和时应包括 力系中所有的力。 以上的平衡方程也可以用三个力矩方程表达 ∑M,=0∑M。=0∑Mc=0 (1.2b) A、B、C是三个任意点,在力的作用平面内这三个点组成一个三角形。 式(1.2)可以广泛运用于结构理论中,尤其是用于确定反作 用力和桁架分析。例1,求解简单吊架ABC受载荷作用下的约束 反力。如图1.22所示,忽略B点摩擦,吊梁受到支持力R。、X, 与Y,的作用,其中X4与Y,分别是在A点处的水平与竖直方向 的未知力。该力系平衡;以A点为矩心,用式(1.2a)得到 X-RB=0 Y,-P-Q=0 Rgc-Pa-Qb=0 由这些公式可以推出:X4=R。=Pa/c+Qb/c与Y4=P+Q。 第二个例子,桁架载荷如图1.23所示,求杆1、2、3的 图1.22 轴力。这里只考虑桁架的阴影部分BCD,把与它连接的杆件1、 2、3用约束反力代替,得到隔离体如图1.23所示。这是五个力的平衡问题,各个力对平面 桁架中任一点的力矩的代数和一定为零。选点A、D、C为矩心,由式(1.2b)得到 S a-Qa-2Qa=0
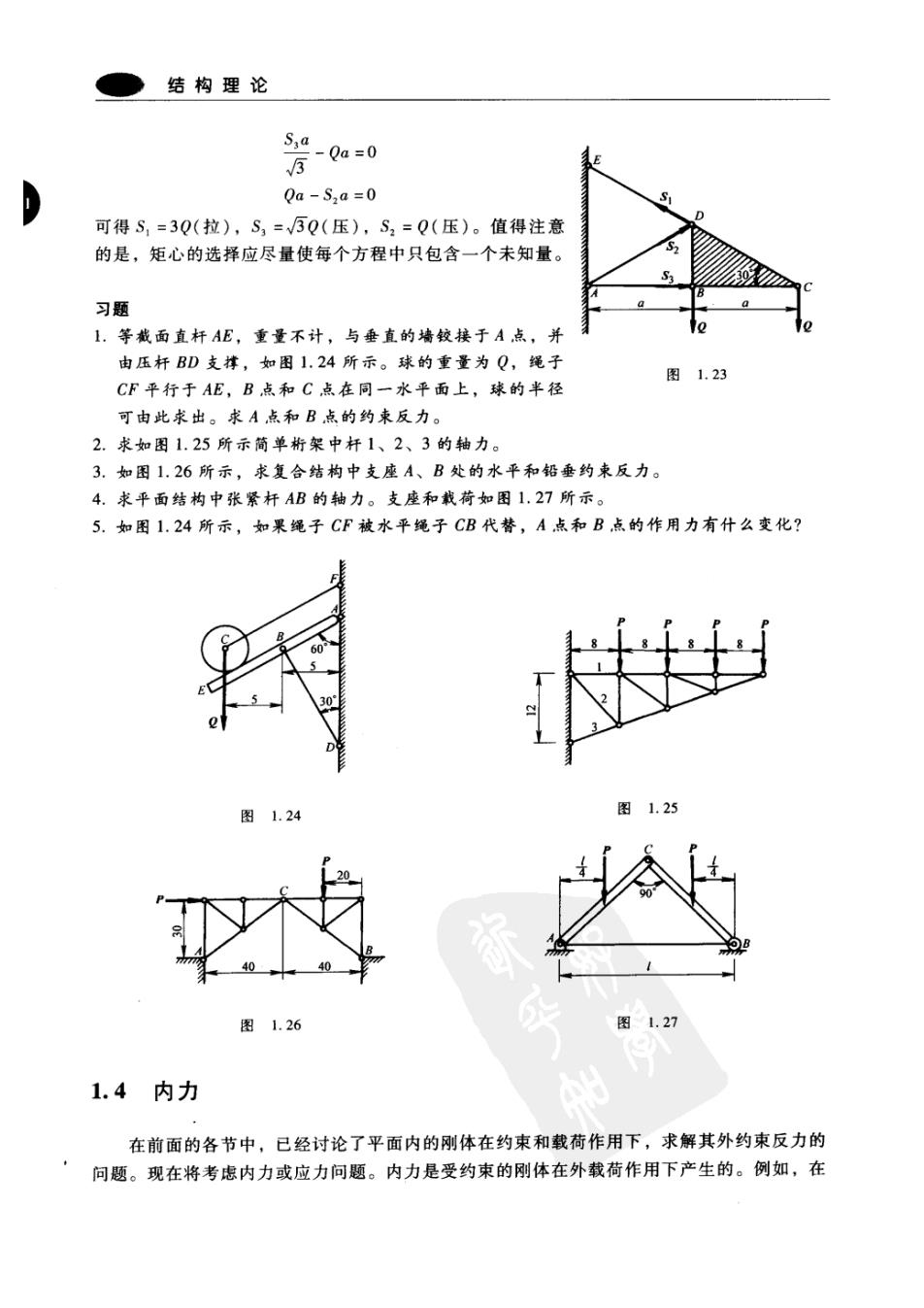
结构理论 S;a -Qa=0 5 Qa-S2a=0 可得S,=3Q(拉),S,=√5Q(压),S2=Q(压)。值得注意 的是,矩心的选择应尽量使每个方程中只包含一个未知量。 习题 1.等戴面直杆AE,重量不计,与垂直的墙较接于A点,并 由压杆BD支撑,如图1.24所示。球的重量为Q,绳子 图1.23 CF平行于AE,B点和C点在同一水平面上,球的半径 可由此求出。求A点和B点的约束反力。 2.求如图1.25所示简单析架中杆1、2、3的轴力。 3.如图1.26所示,求复合结构中支座A、B处的水平和铅垂约束反力。 4.求平面结构中张紧杆AB的轴力。支座和戴荷如图1.27所示。 5.如图1.24所示,如果绳子CF被水平绳子CB代替,A点和B点的作用力有什么变化? 60 图1.24 图1.25 40 图1.26 图1.27 1.4内力 在前面的各节中,已经讨论了平面内的刚体在约束和载荷作用下,求解其外约束反力的 问题。现在将考虑内力或应力问题。内力是受约束的刚体在外载荷作用下产生的。例如,在