
目 录 序 3.6三较拱的影响线………84 译者序 3.7简单析架的影响线…… 87 原著前言 3.8复合析架的影响线………… 91 第1章平面静力学基础…1 第4章弹性体的一般原理…95 1.1平面汇交力系 4.1拉伸、扭转和弯曲的应变能…95 1.2三力平衡 ……………3 4.2登加原理…………97 1.3平衡方程…… 4.3广义形式的应变能… 100 1.4内力…………8 4.4卡氏(Castigliano)第一定理…103 1.5索多边形…12 4.5卡氏(Castigliano)第二定理…106 1.6索多边形的应用…………15 4.6最小功原理……110 1.7分布力作用下的索曲线…18 4.7互等定理 …………………114 1.8柔性悬索……………21 第5章较接桁架的挠度计算…120 1.9弯矩图……25 1.10虚位移原理……… 29 5.1卡氏(Castigliano)定理的应用…120 5.2挠度计算的麦克斯韦一莫尔 第2章静定平面桁架…33 (Maxwell--Mohr)法…123 2.1简单折架…………33 5.3图解法求析架位移…125 2.2反力……35 5.4虚载荷法……131 2.3结点法…38 5.5变异的虚载荷法……135 2.4麦克斯韦(Maxwell)图 40 第6章超静定铰接桁架 ………141 2.5截面法…………43 2.6组合析架………48 6.1概述……141 2.7平面析架的一般理论…52 6.2带一个冗余杆件的析架 …143 2.8复杂析架:亨尼勃格(Henneberg) 6.3带多个冗余杆件的析架 ……147 方法…56 64超静定析架中的装配应力和 2.9虚位移法……60 温度应力 …151 6.5超静定桁架的影响线 …155 第3章影响线 …64 6.6超静定空间结构…159 3.1移动载荷和影响线…64 第7章拱与刚架 ……164 3.2梁支座反力的影响线…68 3.3剪力影响线……72 7.1概述…164 3.4弯矩影响线…76 7.2对称二较拱…165 3.5带有横梁的主梁…80 7.3对称无较拱…169

结构理论 7.4无铰刚架…175 9.4连续梁的矩阵分析…253 7.5有较刚架 …………181 9.5拱和刚架的矩阵方法 …259 7.6温度变化和支座沉降的影响…183 9.6连续刚架的矩阵分析 …264 7.7环…………186 第10章结构动力学…269 第8章连续梁与刚架 …189 10.1单自由度系统的自由振动…269 8.1斜率一挠度方程…189 10.2瑞雷(Rayleigh)法 …273 8.2固端梁… 192 10.3稳态强迫振动…277 8.3连续梁 195 10.4一个干扰力的通用情况…281 8.4变戴面梁… 199 10.5数值积分…… 285 8.5变戴面连续梁………… 205 10.6图形积分……… 289 8.6带等截面杆的简单刚架 212 10.7轨道静动应力… 294 8.7带等栽面杆的连续刚架… 219 10.8等截面梁的横向振动…298 8.8力矩分配法…225 附录 … 302 8.9建筑物刚架分析… 231 8.10带非等戴面杆的刚架…234 附录A国际单位制单位与英美制 单位换算表…302 第9章结构分析的矩阵法…239 附录B习题答素… 304 9.1力法和位移法…239 附录C人名对照表…311 9.2矩阵代数基础…… 241 附录D关键词索引…312 9.3矩阵方法在平面析架中的应用…246 后 装 的

第1章 平面静力学基础 1.1平面汇交力系 结构理论以静力学理论为基础。在本书中,我们认为读者已经熟悉静力学理论,但是因 为静力学理论在分析工程结构问题上的重要作用,还是要复习和回顾一下在工程结构分析中 非常有用的部分静力学原理。首先是力的平行四边形原理:P,和P2两个力,如图1.1a中 的矢量OA和OB,可以合成为一个合力R,合力由以这两个力为边构成的平行四边形的对角 线确定,如图中矢量0C。同样,合力也可以通过力三角形得到,如图1.1b所示。图1.1b 中三角形ABC与图1.1a中的三角形OAC是等同的。 如果平面上的几个力作用在同一点O(见图1.2a),总可以合成为过该点的一个合力。 这个合力可以通过连续应用力平行四边形法则(见图1.2a)确定,或者通过力多边形的闭合 边来确定(见图1.2b)。 图1.1 图1.2 如果力多边形是闭合的,那么合力为零,即给定力系平衡。因此,如果平面汇交力系是 平衡的,则它们的自由矢量组成的力多边形必是闭合的。 上述图形的平衡条件在结构分析中是非常有用的。 举一个简单的例子。如图1.3a所示,一重W的重物受绳索的拉力作用。选环0为自由 体,则环O在W、S,和S2三个力的作用下达到平衡。力S,和S2的方向沿着绳索,它们的 大小称为轴力或拉力。如果重力W的大小已知,则拉力S,和S2的大小可以由图1.3b所示 的封闭的力三角形得到:S,=Wcsca和S2=Wcota
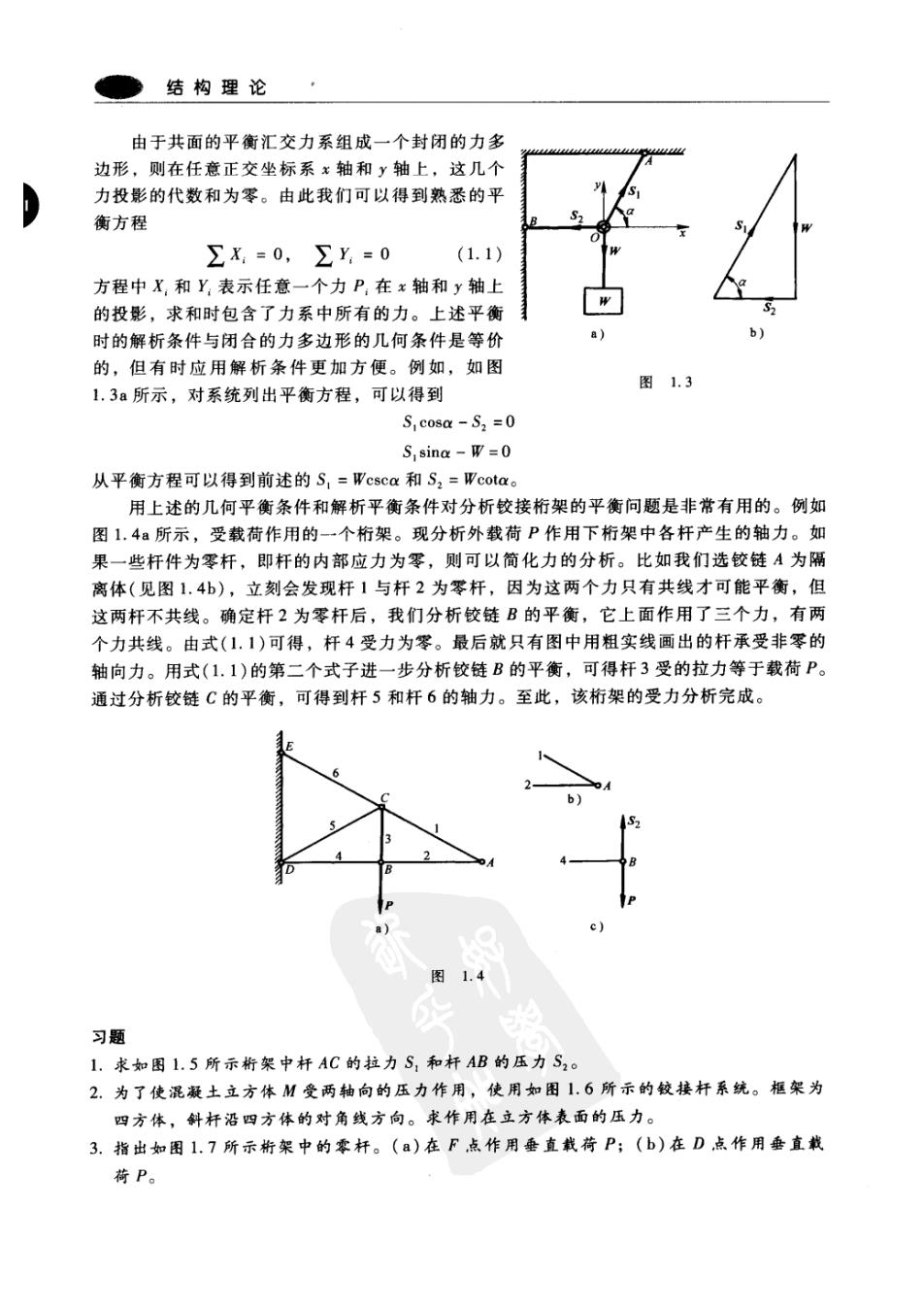
结构理论 由于共面的平衡汇交力系组成一个封闭的力多 边形,则在任意正交坐标系x轴和y轴上,这几个 力投影的代数和为零。由此我们可以得到熟悉的平 衡方程 ∑X=0,∑y=0 (1.1) 方程中X,和Y:表示任意一个力P,在x轴和y轴上 的投影,求和时包含了力系中所有的力。上述平衡 时的解析条件与闭合的力多边形的几何条件是等价 a) 的,但有时应用解析条件更加方便。例如,如图 图1.3 1.3a所示,对系统列出平衡方程,可以得到 S cosa-S2=0 S sina-W=0 从平衡方程可以得到前述的S,=Wesca和S2=Wcota。 用上述的几何平衡条件和解析平衡条件对分析铰接桁架的平衡问题是非常有用的。例如 图1.4所示,受载荷作用的一个桁架。现分析外载荷P作用下桁架中各杆产生的轴力。如 果一些杆件为零杆,即杆的内部应力为零,则可以简化力的分析。比如我们选铰链A为隔 离体(见图1.4b),立刻会发现杆1与杆2为零杆,因为这两个力只有共线才可能平衡,但 这两杆不共线。确定杆2为零杆后,我们分析铰链B的平衡,它上面作用了三个力,有两 个力共线。由式(1.1)可得,杆4受力为零。最后就只有图中用粗实线画出的杆承受非零的 轴向力。用式(1.1)的第二个式子进一步分析铰链B的平衡,可得杆3受的拉力等于载荷P。 通过分析铰链C的平衡,可得到杆5和杆6的轴力。至此,该桁架的受力分析完成。 图1.4 习题 1.求如图1.5所示析架中杆AC的拉力S,和杆AB的压力S2。 2.为了使混凝土立方体M受两轴向的压力作用,使用如图1.6所示的较接杆系统。框架为 四方体,斜杆沿四方体的对角线方向。求作用在立方体表面的压力。 3.指出如图1.7所示析架中的零杆。(a)在F点作用垂直载荷P;(b)在D点作用垂直戴 荷P

第1章平面静力学基础 4.如图1.8所示,将对角线的方向由AD改为BC,则简单析架的作用力有何影响? 5.用实线画出两个简支析架中的主动杆件,戴荷如图1.9所示。 图 1.5 图 1.6 图 1.1 图1.9 1.2三力平衡 同一平面上三个相互不平行的力只有汇交于一点才能处于平衡状态。为证明这个结论, 参考图1.10,力P和Q为汇交于一点0的任意两个力,那么第三个力S与这两个力平衡的 条件是它与这两个力的合力R是大小相等、方向相反且作用在同一条直线上。当然,合力R 必汇交于点O。因此,力S也必过汇交点O。 上述的三力汇交定理对于求解在已知力作用下,刚体 或结构在支座处的约束反力是非常有用的。例如,起重机 如图1.11所示,柱AB由轴承A和B支撑,以使起重机能 绕着垂直轴旋转。在垂直载荷P的作用下,起重机在轴承 A和B处施加压力,而在起重机的支座处产生了大小相 等、方向相反的力作用在起重机上。因此,垂直力P同反 力R,和R。是三力平衡的。忽略在轴承B处的摩擦,反力 图1.10