
第10章土坡稳定性分析 1915年瑞典彼得森(K.E.Petterson)用圆弧滑动法分析边坡的稳 定性。均质的粘性土坡失去稳定是由于滑动土体绕圆心发生转动。把 滑动土体当成一个刚体,滑动土体的重量W,将使土体绕圆心O旋转, 滑动力矩为Ms=WM。 F 抗滑力矩_M-C·L·R 滑动力矩M、 式中 tI- 土的抗剪强度,kPa; L一滑动面滑弧长,m; R—滑动面圆弧半径,m; W一滑动土体的重力,kN/m; x— 滑动土体重心至圆心O的力臂,m。 R 土质学与土力学 33-6 吉林大学建设工程学院
土质学与土力学 33—6 吉林大学建设工程学院 Wx c L R M M F u s r s = = = 滑动力矩 抗滑力矩 1915年瑞典彼得森(K.E.Petterson)用圆弧滑动法分析边坡的稳 定性。均质的粘性土坡失去稳定是由于滑动土体绕圆心发生转动。把 滑动土体当成一个刚体,滑动土体的重量W,将使土体绕圆心O旋转, 滑动力矩为Ms=Wx
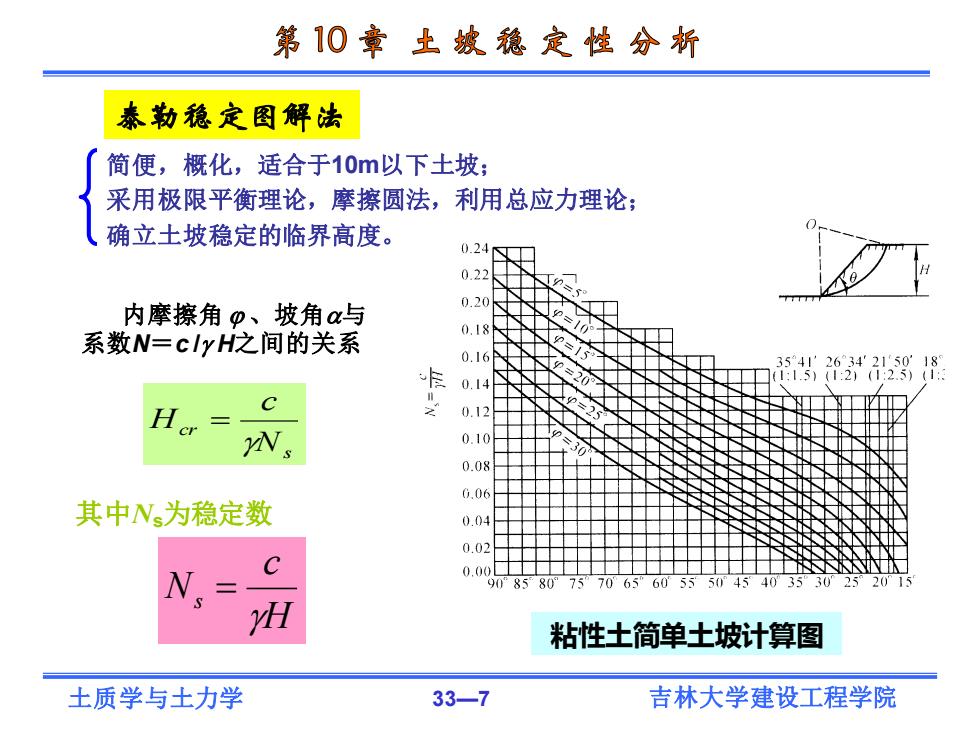
第10章土城稳定性分析 泰勒稳定图解法 简便,概化,适合于10m以下土坡; 采用极限平衡理论,摩擦圆法,利用总应力理论; 确立土坡稳定的临界高度。 0.24 0.22 内摩擦角p、坡角a与 0.20 0.18 系数N=clyH之间的关系 0.16 0.14 丑8 C 0.12 0.10 0.08 6.06 其中Ns为稳定数 0.04 0.02 0.001 90°8580°757065"605550°45 H 粘性土简单土坡计算图 土质学与土力学 33-7 吉林大学建设工程学院
土质学与土力学 33—7 吉林大学建设工程学院 简便,概化,适合于10m以下土坡; 采用极限平衡理论,摩擦圆法,利用总应力理论; 确立土坡稳定的临界高度。 s cr N c H = 粘性土简单土坡计算图 其中Ns为稳定数 泰勒稳定图解法 内摩擦角 、坡角与 系数N=c / H之间的关系 H c Ns =

第10章土坡稳定性分析 【例题10-1】某开挖基坑,深4m, 地基土的重度Y=18kN/m3,有效黏聚力 c=10kPa,有效内摩擦角p=15°。如要求基坑边坡的抗滑稳定安全系数F为1.20。试 问:边坡的坡度设计成多少最为合适? 解:要使抗滑稳定安全系数F=1.20,则基坑边坡的临界高度应为 H。=FH=1.20×4=4.80m N,=c 10 因而 =0.116 yH。18×4.80 由N,=0.116和0=15°查图10-5可得坡角a=59°最为合适。 土质学与土力学 33-8 吉林大学建设工程学院
土质学与土力学 33—8 吉林大学建设工程学院
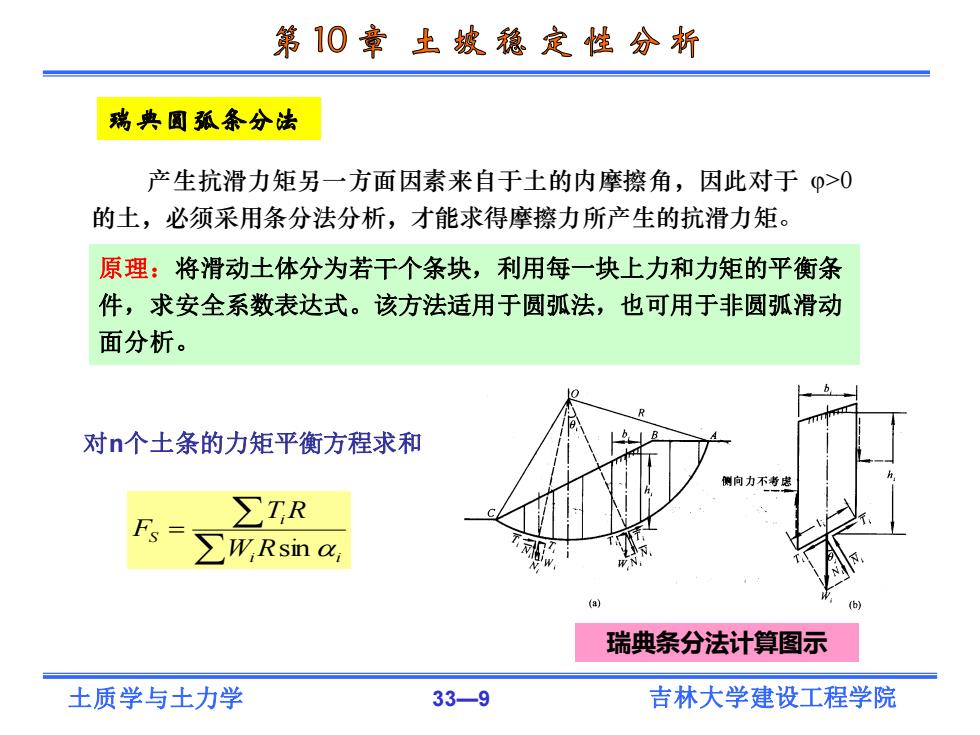
第10章土城稳定性分析 瑞典圆狐条分法 产生抗滑力矩另一方面因素来自于土的内摩擦角,因此对于φ>0 的土,必须采用条分法分析,才能求得摩擦力所产生的抗滑力矩。 原理:将滑动土体分为若干个条块,利用每一块上力和力矩的平衡条 件,求安全系数表达式。该方法适用于圆弧法,也可用于非圆弧滑动 面分析。 对n个土条的力矩平衡方程求和 侧向力不考忠 ∑IR Fs ∑W,Rsin a (a 瑞典条分法计算图示 土质学与土力学 33-9 吉林大学建设工程学院
土质学与土力学 33—9 吉林大学建设工程学院 产生抗滑力矩另一方面因素来自于土的内摩擦角,因此对于 >0 的土,必须采用条分法分析,才能求得摩擦力所产生的抗滑力矩。 原理:将滑动土体分为若干个条块,利用每一块上力和力矩的平衡条 件,求安全系数表达式。该方法适用于圆弧法,也可用于非圆弧滑动 面分析。 瑞典圆弧条分法 瑞典条分法计算图示 对n个土条的力矩平衡方程求和 = i i i S W R T R F sin

第10章土城稳定性分析 条底法向力平衡 N;=W cosa F= (cl,+W,cosa,tanp,】 总应力法求得的 ΣV sin a 土坡稳定卖全集数 其中 smg= R (cl+(W cosa,-ul)tan) 有救应力法求得的 ∑V,sin a 土坡稳定安全集数 土质学与土力学 33-10 吉林大学建设工程学院
土质学与土力学 33—10 吉林大学建设工程学院 Ni Wi i = cos 条底法向力平衡 i i i i i i i s W c l W F sin ( cos tan ) + = 其中 R xi sin i = i i i i i i i i i s W c l W u l F sin ( ( cos )tan ) ' ' + − = 总应力法求得的 土坡稳定安全系数 有效应力法求得的 土坡稳定安全系数