
因此,得到表6.1类型资料的自由度分解式为: (nk-1)=(k-1)+k(n-1) (66) 总自由度DFT=组间自由度DF+组内自由度DFe 求得各变异来源的自由度和平方和后,进而可得: 总的均方 s,=s=∑∑y9 nk-1 组间的均方 s,=52=1 2- (67) k-2 组内均方 8==2g- k(n-1)
因此,得到表6.1类型资料的自由度分解式为: (nk −1)=(k −1)+ k(n −1) (6·6) 总自由度DFT =组间自由度DFt +组内自由度DFe 求得各变异来源的自由度和平方和后,进而可得: (6·7) − − = = − − = = − − = = ( ) ( ) ( ) ( ) 1 2 1 2 2 2 2 2 2 k n y y MS s k n y y MS s nk y y MS s i j i e e i t t i j T T 组内均方 组间的均方 总的均方
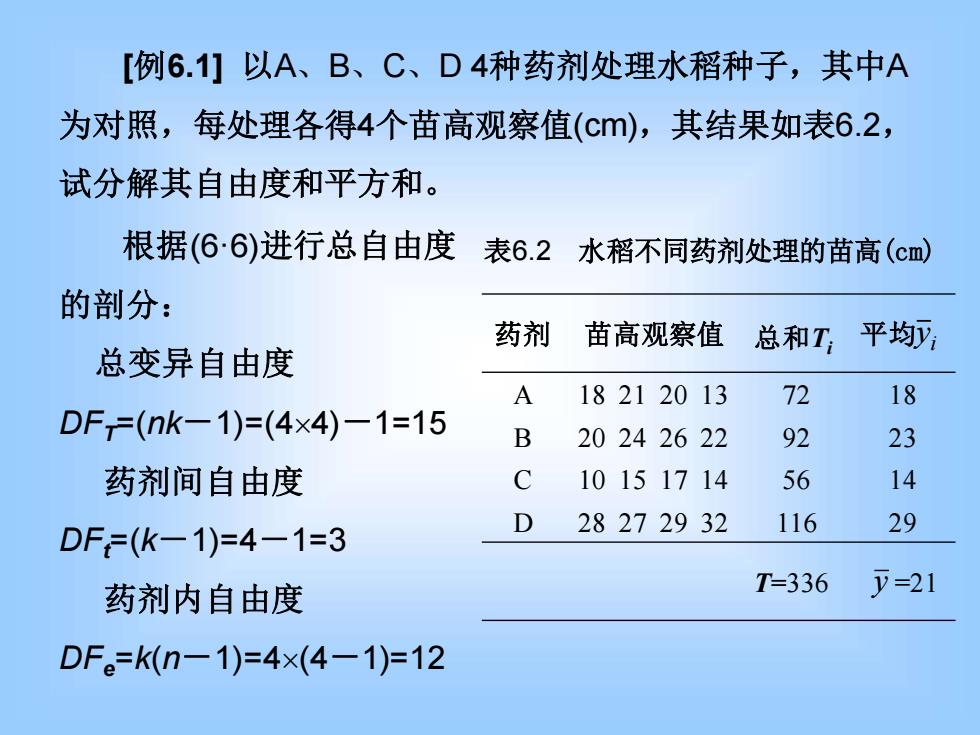
[例6.1]以A、B、C、D4种药剂处理水稻种子,其中A 为对照,每处理各得4个苗高观察值(c),其结果如表6.2, 试分解其自由度和平方和。 根据(66)进行总自由度 表6.2 水稻不同药剂处理的苗高(cm) 的剖分: 药剂 苗高观察值总和T: 平均, 总变异自由度 A 18212013 72 18 DF=(nk-1)=(4×4)-1=15 B 20242622 92 23 药剂间自由度 C 10151714 56 14 DF=(k-1)=4-1=3 D 28272932 116 29 药剂内自由度 T=336 y=21 DFe=k(n-1)=4×(4-1)=12
[例6.1] 以A、B、C、D 4种药剂处理水稻种子,其中A 为对照,每处理各得4个苗高观察值(cm),其结果如表6.2, 试分解其自由度和平方和。 表6.2 水稻不同药剂处理的苗高(cm) 药剂 苗高观察值 总和Ti 平均 A 18 21 20 13 72 18 B 20 24 26 22 92 23 C 10 15 17 14 56 14 D 28 27 29 32 116 29 T=336 =21 i y y 根据(6·6)进行总自由度 的剖分: 总变异自由度 DFT=(nk-1)=(44)-1=15 药剂间自由度 DFt=(k-1)=4-1=3 药剂内自由度 DFe =k(n-1)=4(4-1)=12

根据(63)进行总平方和的剖分: C-T2-336 =7056 nk4×4 SS=∑∑号-C=182+212++322-C=602 s,=n20-2=∑T2/n-C =(722+922+562+1162)/4-C=504 或 SS,=4×[18-21)2+(23-21)2+(14-21)2+(29-21)2]=504 -220,-6-立4 =SS7-SS=602-504=98
根据(6·3)进行总平方和的剖分: 7056 4 4 336 2 2 = = = nk T C 18 21 32 602 2 2 2 2 SST =yi j −C = + ++ −C = (72 92 56 116 ) 4 504 ( ) 2 2 2 2 1 2 2 = + + + − = = − = − / C SS n y y T n C k t i i 或 4 [(18 21) (23 21) (14 21) (29 21) ] 504 2 2 2 2 SSt = − + − + − + − = 602 504 98 ( ) 1 1 1 1 2 2 2 = − = − = = − = − T t k n n k k e i j i i j i SS SS SS y y y T n

或 药剂A内:SS。=182+212+202+132-72/4=38 药剂B内:SS。,=202+242+262+222-92/4=20 药剂C内:SS。,=102+152+17+142-562/4=26 药剂D内:SS。=282+27+292+322-1162/4=14 所以 59.=22,-P=38+20+26+14=98 进而可得均方: MS,=s7=602/15=40.13 MS,=s2=504/3=168.00 MS。=s=98/12=8.17
或 药剂A内: 药剂B内: 药剂C内: 药剂D内: 18 21 20 13 72 4 38 2 2 2 2 2 1 SSe = + + + − = 20 24 26 22 92 4 20 2 2 2 2 2 2 SSe = + + + − = 10 15 17 14 56 4 26 2 2 2 2 2 3 SSe = + + + − = 28 27 29 32 116 4 14 2 2 2 2 2 4 SSe = + + + − = 所以 = − = + + + = k n e i j i SS y y 1 1 2 ( ) 38 20 26 14 98 进而可得均方: 602 15 4013 2 MS s / . T = T = = 504 3 168 00 2 MS s / . t = t = = 98 12 817 2 MS s / . e = e = =

二、F分布与F测验 在一个平均数为4、方差为。2的正态总体中,随机抽 取两个独立样本,分别求得其均方S12和S22,将S2和S22 的比值定义为F: F)=s/s好 (68) 此F值具有s2的自由度,和S22的自由度2。 所谓F吩布,就是在给定的y,和2下按上述方法从正 态总体中进行一系列抽样,就可得到一系列的F值而作成 一个分布。 米F分布下一定区间的概率可从已制成的统计表查出
二、F分布与F测验 在一个平均数为 、方差为 的正态总体中,随机抽 取两个独立样本,分别求得其均方 s1 2 和 s2 2,将 s1 2 和 s2 2 的比值定义为F: 2 2 2 2 ( ) 1 F = s s 1 , 2 (6·8) 此F值具有s1 2 的自由度 v1 和 s2 2 的自由度 v2。 所谓F分布,就是在给定的 v1 和 v2 下按上述方法从正 态总体中进行一系列抽样,就可得到一系列的F 值而作成 一个分布。 F分布下一定区间的概率可从已制成的统计表查出