定积分及其应用:定积分的定义.定积分存在定理的叙 述定积分的性质.定积分的中值定理.定积分作为变上 限的函数及其求导定理.牛顿(Newton 彭布尼芯 (Leibni2)公式定积分的换元法与分 部积分法两种 义积分的定义定积分在几何学中应用(面积、弧长 旋转体体积、已知平行截面面积求体积等)定积分在 物理学中的应用举例 领会:理解原函数概念,理解不定积分和定积分的概念 以及应1的性质 分析: 不定积分的基本公式,掌握不定积分和定积 分的换元法和分部积分法,掌握较简单的有理函数的积 综合:理解变上限的定积分作为其上限的函数及其求导 定理,熟悉牛顿(Newton 莱布尼兹(Leibniz 评价:了解广义积分的概念并会计算广义积分 第力.章常微分方程 知道:微分方程的一般概念:微分方程的定义阶解 通解初始条件特解 ,变量可分离的方程线性方程用变量置 换法解 阶方程举 .全 分方程 领会:了解微分方程及其解、阶、通解、初始条件和特支撑课程 解笔概今 目标1、2 应用:掌握变量可分离方程及一阶线性方程的解法 3、4 12 分析:会解齐次方程和贝努利方程和全微分方程,会用 间 单的变量代换求解某些微分方程 综合:理解线性微分方程解的性质及解的结构 评价:掌握自由项为多项式、指数函数、正弦函数、余 弦函数以及它们的和与乘积的二阶常系统非齐次线性 方程的解法 合计 48 项目名称、主要内容及开设要求 支撑课程 学时 目标 分配 实验一*(必做) 支撑课程 空哈目的. 实验任务 目标1、2、 2 2 实验 实训 内容 实验二幸(选做) 支撑课程 实验目的: 目标1、2、 2 实验任务: 3 合计 H 支撑课程时长 实践内容(含 实践主要内容和要求 目标 分配 教育实习、见(一)实习形式与准备
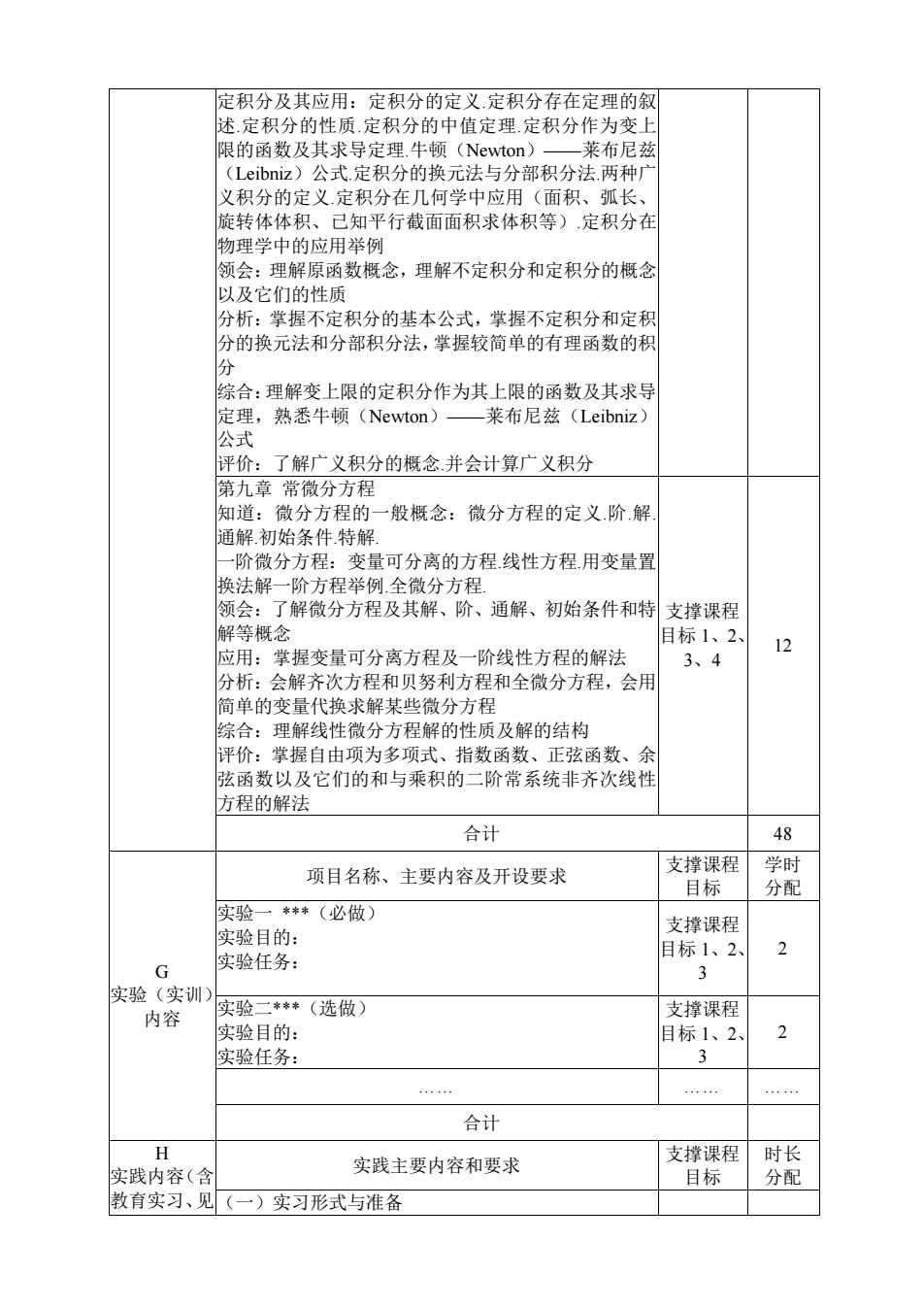
定积分及其应用:定积分的定义.定积分存在定理的叙 述.定积分的性质.定积分的中值定理.定积分作为变上 限的函数及其求导定理.牛顿(Newton)——莱布尼兹 (Leibniz)公式.定积分的换元法与分部积分法.两种广 义积分的定义.定积分在几何学中应用(面积、弧长、 旋转体体积、已知平行截面面积求体积等).定积分在 物理学中的应用举例 领会:理解原函数概念,理解不定积分和定积分的概念 以及它们的性质 分析:掌握不定积分的基本公式,掌握不定积分和定积 分的换元法和分部积分法,掌握较简单的有理函数的积 分 综合:理解变上限的定积分作为其上限的函数及其求导 定理,熟悉牛顿(Newton)——莱布尼兹(Leibniz) 公式 评价:了解广义积分的概念.并会计算广义积分 第九章 常微分方程 知道:微分方程的一般概念:微分方程的定义.阶.解. 通解.初始条件.特解. 一阶微分方程:变量可分离的方程.线性方程.用变量置 换法解一阶方程举例.全微分方程. 领会:了解微分方程及其解、阶、通解、初始条件和特 解等概念 应用:掌握变量可分离方程及一阶线性方程的解法 分析:会解齐次方程和贝努利方程和全微分方程,会用 简单的变量代换求解某些微分方程 综合:理解线性微分方程解的性质及解的结构 评价:掌握自由项为多项式、指数函数、正弦函数、余 弦函数以及它们的和与乘积的二阶常系统非齐次线性 方程的解法 支撑课程 目标 1、2、 3、4 12 合计 48 G 实验(实训) 内容 项目名称、主要内容及开设要求 支撑课程 目标 学时 分配 实验一 ***(必做) 实验目的: 实验任务: 支撑课程 目标 1、2、 3 2 实验二***(选做) 实验目的: 实验任务: 支撑课程 目标 1、2、 3 2 …… …… …… 合计 H 实践内容(含 教育实习、见 实践主要内容和要求 支撑课程 目标 时长 分配 (一)实习形式与准备

月、研习,专(二)实习内容 业实习、毕业l.教学工作实习 论文或毕业2班主任工作实习 设计等) 3教研实习 (三)实习要求 4 理论课全部采用多媒体教学,应用自编或改编的多媒体课件,加上一些 CD动画,改善理论果的枯操和沉闷,吸引学生的注意力,加强授课效 开通网络课堂,达到与学生及时沟通、交流的目的。同时重视师生互动 教学方法与 与小组活动,组织课堂小组讨论和论文写作等活动,将课堂教学变为 教学方式 师生共同活动的过程。 6 主要方气式, ☑讲授☑网络学习☑讨论或座谈口问题导向学 回分组合作学习口专题学习 回实作学习口发表学习 口实习口参观访问口其它: (如口头训练等) (如时间、地点安排与“一课双师”等教师配备需求等) 教学条件 需求 考核方式 课程 课程目标 作业实验期中小组 期末 考试 分目 及评分占 考核内容 评分 标的 比 占比 评分 占比 达成 (%) (%) % 1,对掌握高等数学的基本理论 理程月标的堂根」 5 (13% 课程目标及 2对高等数学基本理论的掌握 和综合运用。 甘老核内突 1.培养抽象概括问题的能力、 考核方式及 逻辑推理能力、空间想象能力 评分占比 课程目标 和自学能力。 P 8 15 2(410% 2对高等数学基本技术的掌握 和综合运用 1.主动对高等数学知识进行学 课程目标习。 3(22%)2.能够就高等数学相关问题进 6 4 行思考、表达和沟通。 1.对高等数学发展史及国内外 课程目标发展现状和趋势的了解。 5 4(11%)2.对高等数学实际应用案例的 解
习、研习,专 业实习、毕业 论文或毕业 设计等) (二)实习内容 1.教学工作实习 2.班主任工作实习 3.教研实习 (三)实习要求 I 教学方法与 教学方式 4. 理论课全部采用多媒体教学,应用自编或改编的多媒体课件,加上一些 CD 动画,改善理论课的枯燥和沉闷,吸引学生的注意力,加强授课效 果。 5. 开通网络课堂,达到与学生及时沟通、交流的目的。同时重视师生互动 与小组活动,组织课堂小组讨论和论文写作等活动,将课堂教学变为 师生共同活动的过程。 6. 主要方式: 讲授 网络学习 讨论或座谈 问题导向学 分组合作学习 专题学习 实作学习 发表学习 实习 参观访问 其它: (如口头训练等) J 教学条件 需求 (如时间、地点安排与“一课双师”等教师配备需求等) 2. 2. 3. K 课程目标及 其考核内容、 考核方式及 评分占比 课程目标 及评分占 比 考核内容 考核方式 课程 分目 标的 达成 度 作业 评分 占比 (% ) 实验 评分 占比 (% ) 期中 考试 评分 占比 (%) 小组 活动 评分 占比 (%) 期末 考试 评分 占比 (% ) 课程目标 1(13%) 1.对掌握高等数学的基本理论 的掌握。 2.对高等数学基本理论的掌握 和综合运用。 2 4 2 5 - 课程目标 2(41%) 1. 培养抽象概括问题的能力、 逻辑推理能力、空间想象能力 和自学能力。 2.对高等数学基本技术的掌握 和综合运用 8 8 10 15 - 课程目标 3(22%) 1.主动对高等数学知识进行学 习。 2.能够就高等数学相关问题进 行思考、表达和沟通。 2 6 4 10 - 课程目标 4(11%) 1.对高等数学发展史及国内外 发展现状和趋势的了解。 2.对高等数学实际应用案例的 理解。 4 2 5 -

1对高等数学科学问题的理解, 课程目标2对高等数学相关问题的分析 4 5 5(13%)能力 B.高等数学原理的应用 总分 201618640 1.自主学习。建议学生通过预习教材,并通过网络、图书馆自主查阅课程中 涉及的学习资源,独立规划自己的课程学习计划,充分发挥自身的学习能 动性。 学习建议2.研究性学习。鼓励学生针对课程教学内容,尝试理论课结合专题报告的教 学方式,开展相关的生物化学进展和专题讲座,提高学生的学习兴趣,了 解国内外最新生化知识,开阔学生的视野。 M 评分量表 《*》课程目标评分量表见附表 备注 课程大纲A一M项由开课学院审批通过,任课教师不能自行更改。 课程教学大纲修订负责人及教学团队系主任审核意见: 成员签名: 杨州 网爱鱼刻 同意 审 意见 系主任签名: 泳明游 2022年8月23日 2022年8月23日
课程目标 5(13%) 1.对高等数学科学问题的理解。 2.对高等数学相关问题的分析 能力。 3.高等数学原理的应用。 4 4 5 - 总分 20 16 18 6 40 - L 学习建议 1.自主学习。建议学生通过预习教材,并通过网络、图书馆自主查阅课程中 涉及的学习资源,独立规划自己的课程学习计划,充分发挥自身的学习能 动性。 2.研究性学习。鼓励学生针对课程教学内容,尝试理论课结合专题报告的教 学方式,开展相关的生物化学进展和专题讲座,提高学生的学习兴趣,了 解国内外最新生化知识,开阔学生的视野。 M 评分量表 《**》课程目标评分量表见附表。 备注 课程大纲 A—M 项由开课学院审批通过,任课教师不能自行更改。 审批 意见 课程教学大纲修订负责人及教学团队 成员签名: 2022 年 8 月 23 日 系主任审核意见: 同意 系主任签名: 2022 年 8 月 23 日

附表 《高等数学》课程目标评分量表 良(80sX< 及格(60 课程目标 优(X≥90》 (70≤X<80 ≤X< 不及格(< 90) 60) 70) 课程目标1.掌握能够扎实地掌握基本 能够掌握基本 能够基本掌握基 能够 未能很 基本概念、基本理概念、基本理论和基本概念、基本理论本概念、基本理基本掌握好学握基本 论和基本运算技 运算技能,为学习后继和基本运算技 论和基本运算技部分基本概念、基本理 棵程和进 一步获得数 为学习后 为学习后继 ,基论和基本运 一步获得 学知识奠定必要的数 课程和进 课程和进一步获本理论和算技能,为学 数学知识奠定必学基础:1、函数、极 获得数学知识 得数学知识奠定基本运算啊后继课程 要的数学基础:1、限、连续:2、一元函 奠定必要的数必要的数学基技能,为和进一步获 函数、极限、连续:数微积分学3、常微学基础:1、函础:1、函数、极学习后继得数学知识 2 元函数微积份方程: 4、向量代数 数、极限、连续:限 、连续: 分学:3、常微 和空间解析几何:5、 元函数微元函数微积分 方程:4、向量代多元函数微积分学:6、积分学:3、常学:3、常微分方数学知识函数、极限、 数和空间解析几 无穷级数。 微分方程:4、 程:4、向量代数奠定必要连续:2、 可:5、多元函数 同时要通过各个向量代数和空和空间解析几的数学基元函数微积 微积分学:6、 无教学环节步培学间醒几何, 何:5、多元函数陆:1、函分学:3、常 穷级数 生具有抽象概括问恩 多元函数微积 微积分学:6、 无数 极限 微 方程 同时要通过各个 的能力、逻辑推理能 分学:6、无穷 穷级数。 续:2向量代数和 评分量 教学环节深步培 力、空间相象能力和自级数。 具有比较熟一元函数空间解析几 养学生具有抽象 学能力,还要特别注意 具有抽象练的运算能力和微积分何:5、多元 表 概括问颗的能力 培养学生具有比较熟概括问题的能综合运用所学知学:3、常函数微积 逻辑推理能力」 练的运算能力和综合力、逻辑推理能识去分析问题和微 分 方学: 无穷 间想象能力和自 运用所学, 知识去 分析 空间想象能解决问题的能程: ,向级数等知 学能力,还要特别 )题和解决间题的能力和自学能力。力。 量代数和点。 注意培养学生具 。 空间解析 有比较熟练的运 几何:5 能力和综合 多元函数 用所学知识去分 微积分 析问题和解决问 学:6、无 题的能力。 穷级数等 知识点。 课程目标2. 对于高等数学基对于高等 对于高等数对于 对干言 深入认识高本概念、 其木论和其兰其木今 基高等数学等数学基本 等数学基本概念 本运算技能有深入的基本理论和 基本理论和基本运基本概概念、基本理 基本理论和基本以识。 体运算技能有算技能有一定的念、基本论和基本运 运算技能。 较深入的认识。以识。 理论和基算技能认识 本运算技不够。 能有基本 的认识
附表 《高等数学》课程目标评分量表 M 评分量 表 课程目标 优(X≧90) 良(80≦X< 90) 中(70≦X<80) 及格(60 ≦X< 70) 不及格(< 60) 课程目标 1. 掌握 基本概念、基本理 论和基本运算技 能,为学习后继课 程和进一步获得 数学知识奠定必 要的数学基础:1、 函数、极限、连续; 2、一元函数微积 分学;3、常微分 方程;4、向量代 数和空间解析几 何;5、多元函数 微积分学;6、无 穷级数。 同时要通过各个 教学环节逐步培 养学生具有抽象 概括问题的能力、 逻辑推理能力、空 间想象能力和自 学能力,还要特别 注意培养学生具 有比较熟练的运 算能力和综合运 用所学知识去分 析问题和解决问 题的能力。 能够扎实地掌握基本 概念、基本理论和基本 运算技能,为学习后继 课程和进一步获得数 学知识奠定必要的数 学基础:1、函数、极 限、连续;2、一元函 数微积分学;3、常微 分方程;4、向量代数 和空间解析几何;5、 多元函数微积分学;6、 无穷级数。 同 时 要通 过各 个 教学环节逐步培养学 生具有抽象概括问题 的能力、逻辑推理能 力、空间想象能力和自 学能力,还要特别注意 培养学生具有比较熟 练的运算能力和综合 运用所学知识去分析 问题和解决问题的能 力。 能够掌握基本 概念、基本理论 和基本运算技 能,为学习后继 课程和进一步 获得数学知识 奠定必要的数 学基础:1、函 数、极限、连续; 2、一元函数微 积分学;3、常 微分方程;4、 向量代数和空 间解析几何;5、 多元函数微积 分学;6、无穷 级数。 具有抽象 概括问题的能 力、逻辑推理能 力、空间想象能 力和自学能力。 能够基本掌握基 本概念、基本理 论和基本运算技 能,为学习后继 课程和进一步获 得数学知识奠定 必要的数学基 础:1、函数、极 限、连续;2、一 元函数微积分 学;3、常微分方 程;4、向量代数 和空间解析几 何;5、多元函数 微积分学;6、无 穷级数。 具有比较熟 练的运算能力和 综合运用所学知 识去分析问题和 解 决 问 题 的 能 力。 能 够 基本掌握 部分基本 概念、基 本理论和 基本运算 技能,为 学习后继 课程和进 一步获得 数学知识 奠定必要 的数学基 础:1、函 数、极限、 连续;2、 一元函数 微积分 学;3、常 微分方 程;4、向 量代数和 空间解析 几何;5、 多元函数 微积分 学;6、无 穷级数等 知识点。 未能很 好掌握 基 本 概念、基本理 论 和 基 本 运 算技能,为学 习 后 继 课 程 和 进 一 步 获 得 数 学 知 识 奠 定 必 要 的 数学基础:1、 函数、极限、 连续;2、一 元 函 数 微 积 分学;3、常 微分方程;4、 向 量 代 数 和 空 间 解 析 几 何;5、多元 函 数 微 积 分 学;6、无穷 级 数 等 知 识 点。 课程目标 2. 深入认识高 等数学基本概念、 基本理论和基本 运算技能。 对 于 高等 数学 基 本概念、基本理论和基 本运算技能有深入的 认识。 对于高等 数学基本概念、 基本理论和基 本运算技能有 较深入的认识。 对于高等数 学基本概念、基 本理论和基本运 算技能有一定的 认识。 对 于 高等数学 基本概 念、基本 理论和基 本运算技 能有基本 的认识。 对 于 高 等 数 学 基 本 概念、基本理 论 和 基 本 运 算技能 认 识 不够

课程目标3. 对高等数学发展对高等数对高等数学对高对高等 能够了解高使及国内外发展现状学发展史及国发展史及国内外等数学发数学发展史 等数学发展的趋和趋势有全面的认识:内外发展现状发展现状和趋势展史及国及国内外发 、动态以及与生能够很好的将理论知和趋势有较好有 触实我和社会生极写生产实我和在会识, 定的认识: 内外发展展现状和趋 能够将理论知识现状和趋势认识不足: 活的联系。 生活相联系。 理论知识与生与生实我和社势有认不能铭很 产实践和社会会生活相联系。识:能够的将理论知 生活相联系 在一定程识与生立实 暗上将理残和补△生 论知识与话相联系。 生产实践 和社会生 话相联 系。 课程目标4 具有较好的文献 能够自 能够对文献 能够 能够对 能够对岛等查阅、 整理和分析的能对文献进行查进行查阅、整理对文献进文献进行查 数学基础理论与力,能够自主选择高等阅、整理和分和分析,并选择行查阅、阅、整理和分 实践产生研究兴数学相关课题进行读析,并选择择高择高等数学相关整理和分析,并选择择 橄。 书报告的撰写:文献报等数学相关课课题进行读书报析,并选高等数学相 告质量高,在课堂上进 题进行读书报告的撰写: 文献择择高等关课题进行 行较好的小组讨论。 告的撰写:义 报告质量 般,数学 相关论文报告的 报告质量较高,在课堂上能够完课题进行撰写:文献报 在课堂上能够成小组讨论。 读书报告告质量较差。 进行较好的小 的撰写: 组讨论。 文献报告 质量 胶。 课程目标5. 能够熟练利用课 能够较好 能够利用课 能够 不能利 能够利用课程所学知识分析和解利用课程所学程所学知识分析基本利用用课程所学 程所学知识分析决基础科学研究、应用知识分析和解和解决基础科学课程所学知识分析和 和解决基础科学研发中的择高等数学快基础科学研研究、 应用开发知识分析解决基础利 研究、应用开 发可 可题。 究、应用开发中中的择高等数学 和解决基学研究、应月 的择高等数学问 的择高等数学问题。 础科学研开发中的择 题。 问题。 究、应用高等数学问 开发中的题。 择高等数 子题
课程目标 3. 能够了解高 等数学发展的趋 势、动态以及与生 产实践和社会生 活的联系。 对 高 等数 学发 展 史及国内外发展现状 和趋势有全面的认识; 能够很好的将理论知 识与生产实践和社会 生活相联系。 对高等数 学发展史及国 内外发展现状 和趋势有较好 的认识;能够将 理论知识与生 产实践和社会 生活相联系。 对高等数学 发展史及国内外 发展现状和趋势 有一定的认识; 能够将理论知识 与生产实践和社 会生活相联系。 对 高 等数学发 展史及国 内外发展 现状和趋 势有认 识;能够 在一定程 度上将理 论知识与 生产实践 和社会生 活相联 系。 对高等 数 学 发 展 史 及 国 内 外 发 展 现 状 和 趋 势认识不足; 不 能 够 很 好 的 将 理 论 知 识 与 生 产 实 践 和 社 会 生 活相联系。 课程目标 4. 能够对高等 数学基础理论与 实践产生研究兴 趣。 具 有 较好 的文 献 查阅、整理和分析的能 力,能够自主选择高等 数学相关课题进行读 书报告的撰写;文献报 告质量高,在课堂上进 行较好的小组讨论。 能够自主 对文献进行查 阅、整理和分 析,并选择择高 等数学相关课 题进行读书报 告的撰写;文献 报告质量较高, 在课堂上能够 进行较好的小 组讨论。 能够对文献 进行查阅、整理 和分析,并选择 择高等数学相关 课题进行读书报 告的撰写;文献 报告质量一般, 在课堂上能够完 成小组讨论。 能 够 对文献进 行查阅、 整理和分 析,并选 择择高等 数学相关 课题进行 读书报告 的撰写; 文献报告 质量一 般。 能够对 文 献 进 行 查 阅、整理和分 析,并选择择 高 等 数 学 相 关 课 题 进 行 论 文 报 告 的 撰写;文献报 告质量较差。 课程目标 5. 能够利用课 程所学知识分析 和解决基础科学 研究、应用开发中 的择高等数学问 题。 能 够 熟练 利用 课 程所学知识分析和解 决基础科学研究、应用 开发中的择高等数学 问题。 能够较好 利用课程所学 知识分析和解 决基础科学研 究、应用开发中 的择高等数学 问题。 能够利用课 程所学知识分析 和解决基础科学 研究、应用开发 中的择高等数学 问题。 能 够 基本利用 课程所学 知识分析 和解决基 础科学研 究、应用 开发中的 择高等数 学问题。 不能利 用 课 程 所 学 知 识 分 析 和 解 决 基 础 科 学研究、应用 开 发 中 的 择 高 等 数 学 问 题