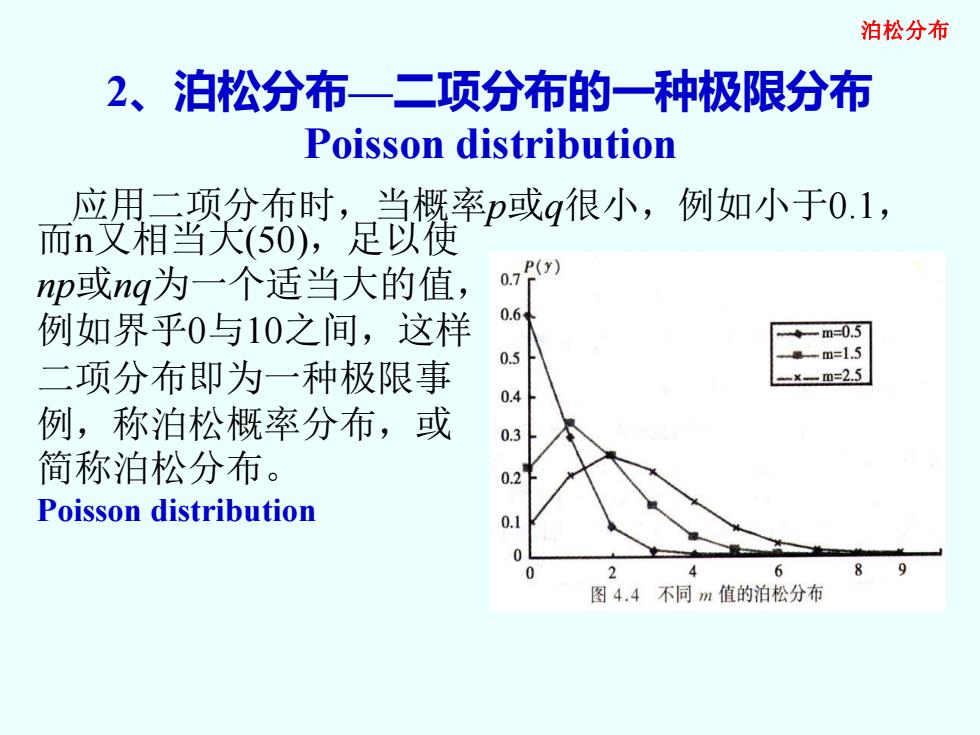
泊松分布 2、泊松分布一二项分布的一种极限分布 Poisson distribution 应用二项分布时,当概率p或q很小,例如小于0.1, 而n又相当天(50),足以使 np或ng为一个适当大的值, 07) 例如界乎0与10之间,这样 0.6 -m=0.5 0.5 最-m=1.5 二项分布即为一种极限事 =×m=2.5 例,称泊松概率分布,或 0.3 简称泊松分布。 0.2 Poisson distribution 0.1 2 6 89 图4.4不同m值的泊松分布
2、泊松分布—二项分布的一种极限分布 Poisson distribution 而n又相当大(50),足以使 np或nq为一个适当大的值, 例如界乎0与10之间,这样 二项分布即为一种极限事 例,称泊松概率分布,或 简称泊松分布。 Poisson distribution 应用二项分布时,当概率p或q很小,例如小于0.1, 泊松分布

泊松分布 如果将np=m,接近分布为: P()=e-m m r N(em+emm+em m te-m m 31 式中,=1,2,.,oo,为任意项的项数。m以平均数估计。 凡观察次数n(相当大),某事件出现的平均次数却很少,则 该事件符合泊松分布。泊松分布的平均数、方差、标准差为: u=m 62=m δ=Wm
如果将np = m,接近分布为: ! ( ) r m p e r m x − = 式中,x=1,2,., ∞,为任意项的项数。m以平均数估计。 凡观察次数n(相当大),某事件出现的平均次数却很少,则 该事件符合泊松分布。泊松分布的平均数、方差、标准差为: = m = m 2 = m ) ! . 2! 3! ( 2 3 r m e m e m N e e m e r −m −m −m −m −m + + + + 泊松分布