
4I0 CALCULUS IN THE EIGHTEENTH CENTURY Euler also answers.For example,Bernoulli had argued that since(-a), then log (-a)3 =log a2 and so 2 log (-a)2 log a or log (-a)log a. Euler counters that,since (av-1)=a',then log a=log(av-1)= log a log v-1 and so in this case,presumably log v-1 would have to be 0.But,Euler says,Bernoulli himself has proved in another connection that logv√-1=V-Iml2. Leibniz had argued that since ⑤ log(1+刘=x-万2+写0-年+. then for x =-2 lg(-)=-2-专-号, from which one sees at least that log (-1)is not 0 (in fact,Leibniz had said that log (-1)is nonexistent).Euler's answer to this argument is that from 1+本=1-*+2-+, for x=-3 one obtains -2=1+3+9+27+. and for *1 one obtains 复=1-1+1-1+. so that by adding the left and right sides 0=2+2+10+26+ Hence,says Euler,the argument from serics proves nothing. After refuting Leibniz and Bernoulli,Euler gives what is,by present standards,an incorrect argument.He writes x=60-(1+), wherein i is an infinitely large number.18 Then =1+智 18.In his earlier work Euler used i (the first letter of infinitus)for an infinitely large quantity.After 1777 he used i for v-1

ELLIPTIC INTEGRALS 41r and so y=(x2-1). Since x,"the root with infinitely large exponent i,"has infinitely many complex valucs,y has such values,and since y log *then so does log x. In fact Euler now writes1 x=a+bW-1=c(cos中+V-1inφ). Letting c be he has x=(cos中+isin)=PeW-ie±2, and so (6) y=lgx=C+(中±2A)V一I where A is a positive integer or zero.Thus,Euler affirms,for positive real numbers only one value of the logarithm is real and the others are all imaginary;but for negative real numbers and for imaginary numbers all valucs of the logarithm are imaginary.Despite this successful resolution of the problem,Euler's work was not accepted.D'Alembert advanced meta- physical,analytical,and geometrical arguments to show that log(-1)=0. 4.Elliptic Integrals John Bernoulli,having succeeded in integrating some rational functions by the method of partial fractions,asserted in the Acta Eruditorum of 1702 that the integral of any rational function need not involve any other tran- scendental functions than trigonometric or logarithmic functions.Since the denominator of a rational function can be an nth degree polynomial in the correctness of the assertion depended on whether any polynomial with real coefficients can be expressed as a product of first and second degree factors with real coefcients.Leibniz in his paper in the Acta of 1702 thought this was not possible and gave the example ofx+a.He pointed out that at=(x-av-1)(x+av1) =(+WW-)(x-W√-) x (x+av-v-I)(x-av-V-I) and,hesaid,no two of thesfour factors multiplied together givea quadratic factor with real coefficients.Had he been able to express the square root of 19.a+W万=v+(o++万va+动-ea+iim机

412 CALCULUS IN THE EIGHTEENTH CENTURY V-I and -V-I as ordinary complex numbers he would have seen his icholas Bernoulli (1687-1759),a nephew of James and John,po out in the Acta Eruditorum of 1719 that (a (a2+x2+axv2)(a2+x2-axv2);thus the function 1/(x4+a)could be integrated in terms of trigonometric and logarithmic functions The integration of irrational functions was also considered.James Bernoulli and Leibniz corresponded on this subject,because such integrands were being encountered frequently.James in16942 was concerned with the elastica,the shape assumed by a thin rod when forces are applied to it-as, for example,at its ends.For one set of end-conditions he found that the equation of the curve is given by (x2+ab)dx dy-Vaabi he could not integrate it in terms of the elementary functions.In connection with this work he introduced the lemniscate,whose rectangular coordinate 盟ae em ue o8 y2)and whose polar coordinate equation to an arbitrary point on the curve is given by a J0a-, and surmised that this integral,too,could not be integrated in terms of the elementary functions.Seventeenth-century attempts to rectify the ellipse whose arc length is important for astronomy,led to the problem of evaluating t(1-k22)d北 5=a0V0-0- when the equation of the ellipse is taken as +=1 and in the integrand k=(a2-62)/a2 andt =x/a.The problem of finding the period of a simple pendulum led to the integral Such irrational integrands also occurred in finding the length of arc of a hyperbola,the trigonometric functions,and other curves.These integrals were already known by 1700;and others involving such integrands kept occurring throughout the eighteenth century.Thus Euler,in a definitive 20.Acta Erud.,1694,262-76=0pera,2,576-600

ELLIPTIC INTEGRALS 43 treatment of the elastica in the appendix to his 1744 book on the calculus of variations,obtained dy (c +Bx+yx2)dx Vai-(a+Bx+yx2) where the constants are for us immaterial.Like his predecessors,he resorted to series in order to obtain physical results. The class of integrals comprised by the above examples is known as elliptic,the name coming from the problem of finding the length of arc of an ellipse.The eighteenth-century men did not know it,but these integrals cannot be evaluated in terms of the algebraic,circular,logarithmic,or exponential functions.21 The first investigations of elliptic integrals were directed not so much toward attempts to evaluate the integrals as toward the reduction of the more complicated ones to those arising in the rectification of ellipsc and hyperbola.The reason for this approach is that from the geometrical point of view,which dominated at that time,the integralsfor the clliptic and hyperbolic arcs seemed to be the simplest ones.A new point of view was opened up by the observation that the differential equation (7) f(x)d=±f(y), whereff()dx is a logarithmic function or an inverse trigonometric function, has as an integral an algebraic function of and y;that is,in spite of the fact that it isimpossible to find an algebraic integral off(itsefone can find an algebraic integral of the sum or difference of two such differentials. John Bernoulli then asked whether this property might not hold for other integrals than those of logarithmsor inverse trigonometric functions.He had discovered in 1698 that the difference of two arcs of the cubical parabola (y=)is integrable,a result he had obtained accidentally and regarded as most elegant.He then posed the more general problem of finding arcs of (higher)parabolas,ellipses,and hyperbolas whose sum or difference is equal to a rectilinear quantity,and affirmed that parabolic curves of the form amy=b"x,m +p =n+g,are such that arcs of such curves,added or subtracted,equal a straight line.He gave no proof. Count Giulio Carlo de'Toschi di Fagnano (1682-1766),an amateur mathematician,began in 1714 to take up these problems.23 He considered the curvesy=(2/m +2)xm+1/am with m rational.For such curves it is rather straightforward to show (Fig.19.1)that )arc PP:-(PR -PR) m个1 dx 21.This was proved by Liouville (Jour.de 'EcolePoly 14,1833,124-93). 22.Acta Erud.,0ct.1698,462E.=0pra,1,249-53. 23.Giornale dei Letterati d'Italia,Vols.19 ff
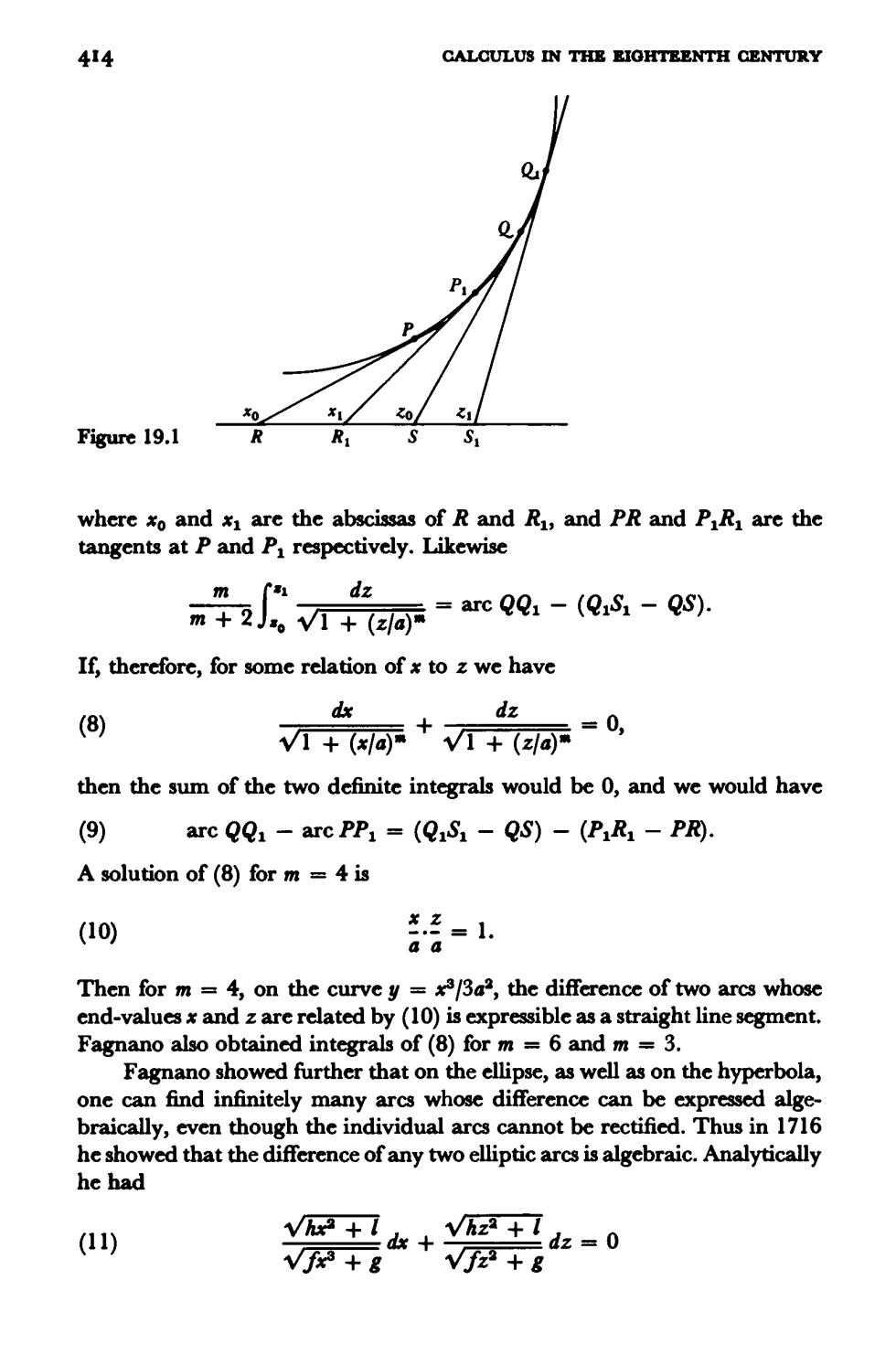
414 CALCULUS IN THE EIOHTEENTH CENTURY Figure 19.1 RR where xo and are the abscissas of R and R,and PR and PR are the tangents at P and P respectively.Likewise 干2v十g=ac0-Qs-Q dz If,therefore,for some relation of x to z we have dx (8) dz V1+网+V+z0=0, then the sum of the two definite integrals would be 0,and we would have ⊙ arc QQ-arc PP=(QS-QS)-(PR1 -PR). A solution of (8)for m =4 is (10) 经=1 Then for m=4,on the curve y =33a2,the difference of two arcs whose end-values*and z are related by(10)is expressible as a straight line segment. Fagnano also obtained integrals of(8)for m =6 and m=3. Fagnano showed further that on the ellipsc,as well ason the hyperbola, one can find infinitely many arcs whose difference can be expressed alge- braically,even though the individual arcs cannot be rectified.Thus in 1716 he showed that the difference of any two elliptic arcs is algebraic.Analytically he had (11) y+k+y2+z=0 √按+8 vf+&