
率为在束缚轨道上电子旋转的经典频率之半的整数倍,玻尔用牛 顿力学推导了氢原子的能级公式。用(1.2),他得到了与观察到的 氢光谱一致的结果。但是,把玻尔理论适用于氦光谱的尝试是失 败了。而且,此理论不能用于说明分子中的化学键。 玻尔模型的根本困难在于用经典牛顿力学去说明原子中电子 的运动。显示不连续频率的原子光谱数据表明只有某些能量的运 动是允许的,即,电子的能量是“量子化”的。而牛顿力学允许能量 有连续变化范围。波动运动中的确出现量子化;例如,提琴弦的基 音和泛音频率。因此,德布罗意(de Broglie)于1923年提出电子 的运动可能有波的样子;即一个质量m和速率v的电子有一波长 入与之相联系,为 2=b三b (1.3) mo p 式中p是线动量。德布罗意用与光子类比的推理得出(1.3)式*。根 据爱因斯坦狭义相对论,任何粒子(包括光子)的能量可以表示为 E=mc2,其中c是光速。对于一个以速率c运动的光子,用(1.1) 得mc2=v=hc/,所以=h/mc=b/p。因而(1.3)式是电子的 相应的关系式。 1927年,Davison和Germer由观察从金属上反射的电子的 衍射效应,从实验上证实了德布罗意假说。1932年,Stern用氨原 子和氢分子观察到了同样的效应,这证明了波的效应不是电子独 有的,而是作为微观粒子运动的普遍规律的结果。(电子显微镜是 电子波动性的一个实际应用。) 电子在某些方面表现象粒子,在另些方面表现象波。我们面对 着物质(和光)的好似矛盾的“波-粒二象性”。怎能既是一个粒 子一一定域的实体,又是一个离域的被呢?回答是:电子既不是一 *译者注:原书中Eq.(X.X)一律译为(X.X)式
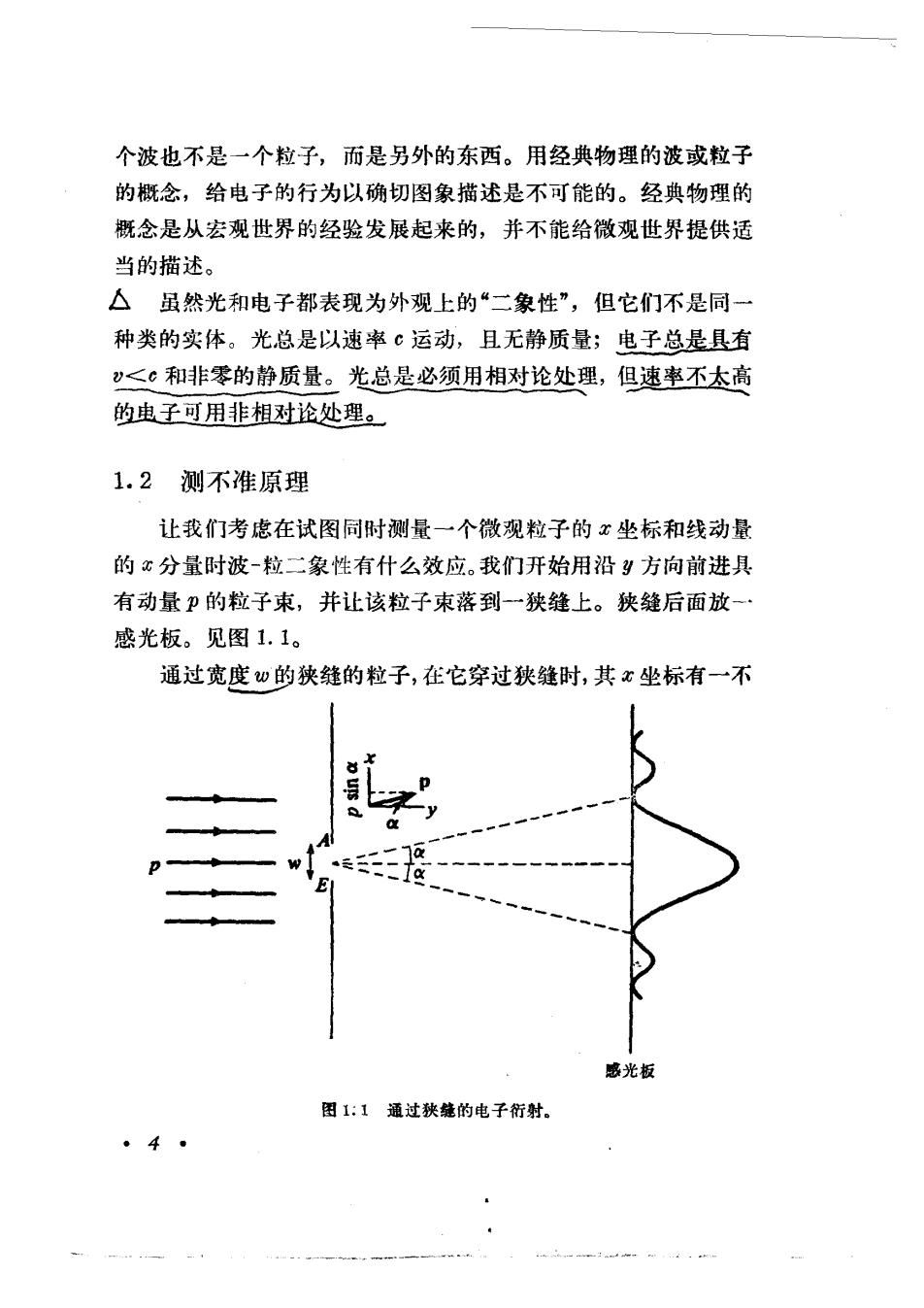
个波也不是一个粒子,而是另外的东西。用经典物理的波或粒子 的概念,给电子的行为以确切图象描述是不可能的。经典物理的 概念是从宏观世界的经验发展起来的,并不能给微观世界提供适 当的描述。 △虽然光和电子都表现为外观上的“二象性”,但它们不是同一 种类的实体。光总是以速率c运动,且无静质量;电子总是具有 <¢和非零的静质量。光总是必须用相对论处理,但速率不太高 的电子可用非相对论处理。 1.2 测不谁原理 让我们考虑在试图同时测量一个微观粒子的x坐标和线动量 的c分量时波-粒二象性有什么效应。我们开始用沿!方向前进具 有动量p的粒子束,并让该粒子束落到一狭缝上。狭缝后面放-· 感光板。见图1.1。 通过宽度w的狭缝的粒子,在它穿过狭缝时,其心坐标有一不 P 感光板 图1:1通过狭缝的电子衍射。 4

确定值0。称此x的展宽值为△,有△x=”。了二山) 由于微观“粒子”有波被动性,它们被狭缝衍射,在板上产生(象 光束那样)衍射图样。图1.1中,图线的高是到达指定点的粒子数 目的量度。衍射图样指出,当粒子被狭缝衍射时,它们的运动方向 改变了,从而一部分动量转移到x方向。动量的x分量是由动量 矢量在x方向的投影给出。一个向上偏转α角的粒子具有动量的 x分量为psina。一个向下偏转&角的粒子具有动量的x分量 一psina。由于多数粒子在一c到a范围内发生偏转,其中&是到 衍射图第一个最小处之角,因此我们取在中央行射峰展宽的动量 值之半作为动量的x分量的不确定值△Pz的量度:△pz=psinc。 于是 △xAPx=pwsina (1.4) 发生衍射第一最小的角度是容易计算的。第一最小的条件是: 在缝的上边缘通过缝的粒子与通过缝中央的粒子所经过的距离差 等于受,入是与粒子相联系的波的波长。从狭缝顶端发出的波和 从狭缝中心发出的波正好位相相反而彼此相消。从狭缝中点之下 距离d处发出的波与狭缝顶端之下距离d处发出的波相消。在图 1.2中作AC,使AD=CD,则路程长度之差为BC。狭缝到屏的距 图1.2第一最小衍射的计算

离比缝宽要大。因而AD与BD几乎平行。这使得角ACB基本上 是一直角,所以角BAC=&。于是路程差BC是wsin&。o令BC= 号1,得0sina=2,(1.4)式变为△Ap:=p。波长入由德布罗意 关系给出,1=h/p,于是△x△pz=h。由于不确定度尚未精确定义, 等号不真正确切,代之而写为 △x△p≈h (1.5) 这指出x和Px的不确定度的乘积是普朗克常数的数量级。在5.1 节中,我们将给出不确定度的精确的统计定义和精确的不等式以 代替(1.5)。 虽然我们只用了一个实验装置来说明(1.5),但它的正确性是 普遍的。不管做怎样的尝试,微观“粒子”的波-粒二象性对于我们 同时测定这样的粒子的位置和动量的能力是加有限制。位置测定 得愈精确,则动量测定得愈不精确。(在图1.1中,sina=/w,所 以狭缝变窄则增大衍射图样的宽展。)这个限制叫做测不准原理, 在1927年由海森堡(Heisenberg)发现。 由于波-粒二象性,测量动作在被测系统中引入一不可控制的 扰动。我们开始时用具有一精确P值(譬如为零)的粒子,由于加 一个狭缝,我们测量粒子的x坐标到准确度w,但此测量引入一不 确定度于粒子的Px值中,这个测量改变了体系的态。 1.3含时间的薛定谔方程 经典力学只适用于宏观粒子。对于微观“粒子”,需要一个新 形式的力学,叫做量子力学(或波动力学)。现在考虑经典力学与 量子力学之间的一些对比。为简单起见,我们处理一维的一粒子 体系。 经典力学中粒子的运动服从牛顿第二定律: 6●

d2x F=m dt? (1.6) 式中F是作用于粒子的力,m是粒子的质量,t是时间。(1.6)式 含有坐标x对t的二阶导数。要解它必须进行两次积分。这样在 解中引入二个任意常数c1和c2,于是 =g(t,c1,C2) (1.7) 9是飞的某个函数。现在问,在给定时刻t。必须具有什么情况才 能预知粒子的未来运动?如果知道在t0时粒子在x0点,则有 x0=9(t0,C1,c2) (1.8) 由于有两个常数要确定,还需要知道更多的情况。微分(1.7),可 得 =0=品9,c,) dx 式中)是粒子的速度。如果也知道在t。时粒子具有速度0,于 是有另外一个关系式 d gi9(t,c1,c2) (1.9) 则我们可用(1.8)和(1.9)去解c1和c2,以和t0表示。知道了 c1和c2,可用(1.7)式去预期粒子确切的未来运动。 “态”字在经典力学中意味着体系的每个粒子在某一瞬间有确 定的位置和速度,以及有确定的力作用于粒子上。按牛顿第二定 律,给出在任何时刻体系的态,它的未来的态和未来的运动是完 全确定的。牛顿力学在解释天体运动时的深刻成功,使得许多哲 学家用牛顿定律作为哲学决定论的论据。数学家与天文学家 Laplace(1749一1827)认为字宙只不过是由服从牛顿定律的粒子 所组成。所以,给定某时刻字宙的状态,字宙中一切事物的未来运 动是完全决定了的。若有超然能力知道在任一时刻字宙的状态, 就可在原则上计算所有的未来运动