e Center for Theoretical Chemical Physics Laboratory of molecular Catalysis Innovative material (1)正态克体u的置信区间(o已和) f(x) 0.4 单侧问题: 如果被估计的总体均值 u藏在≥x或是≤H区间 01241-a 内的话,那就是单侧问 题它们的置信限应是: XU=UCL=X+Z n f(x) 0.4 xLCL=x-。 0.241-a -3 -2 0 2 3 X 振华 数理统1仕忆子中W凹用 造
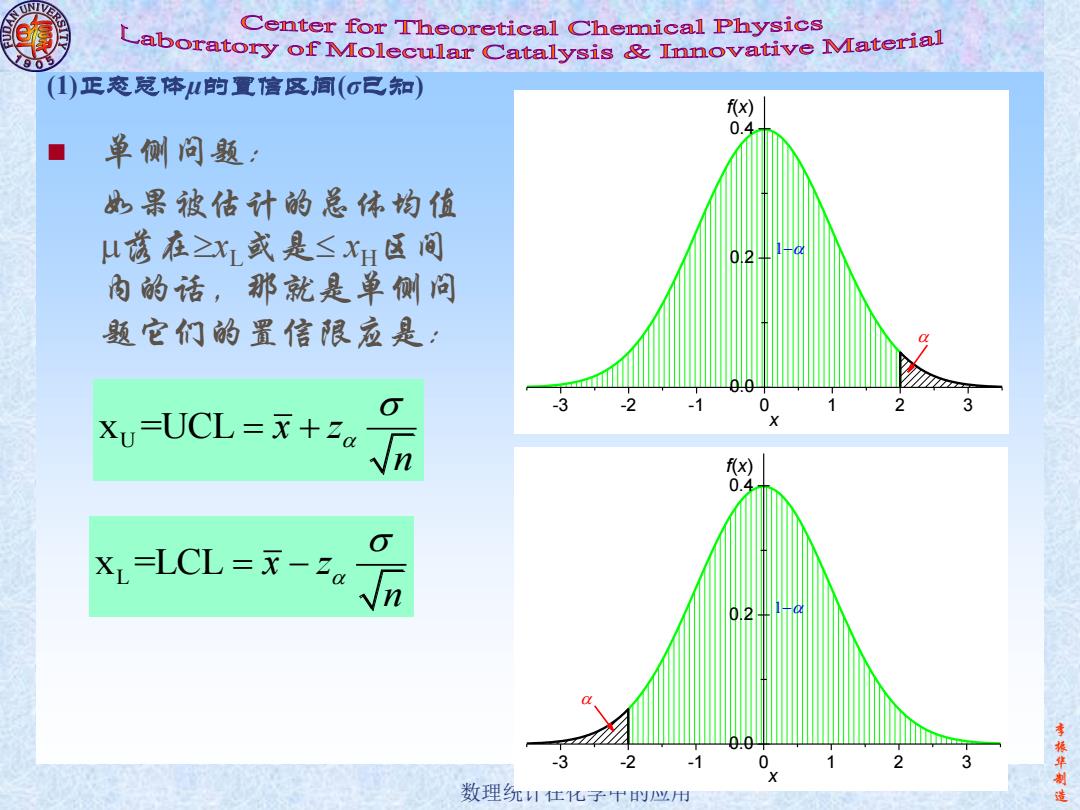
李 振 华 制 数理统计在化学中的应用 造 (1)正态总体µ的置信区间(σ已知) 单侧问题: 如果被估计的总体均值 落在xL或是 xH区间 内的话,那就是单侧问 题它们的置信限应是: U x =UCL x z n L x =LCL x z n -3 -2 -1 0 1 2 3 0.0 0.2 0.4 x f(x) -3 -2 -1 0 1 2 3 0.0 0.2 0.4 x f(x)
Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Inovative Material 1例3-2 为测得一标准物质中某元素含量,对它共进行了80次 的测定,得到样品中该元素的平均含量为12.73%,标 准偏差为0.056%,试问由此而得到的总体均值在概率 为95%的情况下,应小于何值? 解:单侧问题: x=12.73% 6=0.056% n=80 0.056 UCL=x+za =12.73+1.645× n √80 有95%的可能≤12.74% =12.73+0.01 =12.74 李振华制 数理统计在化学中的应用
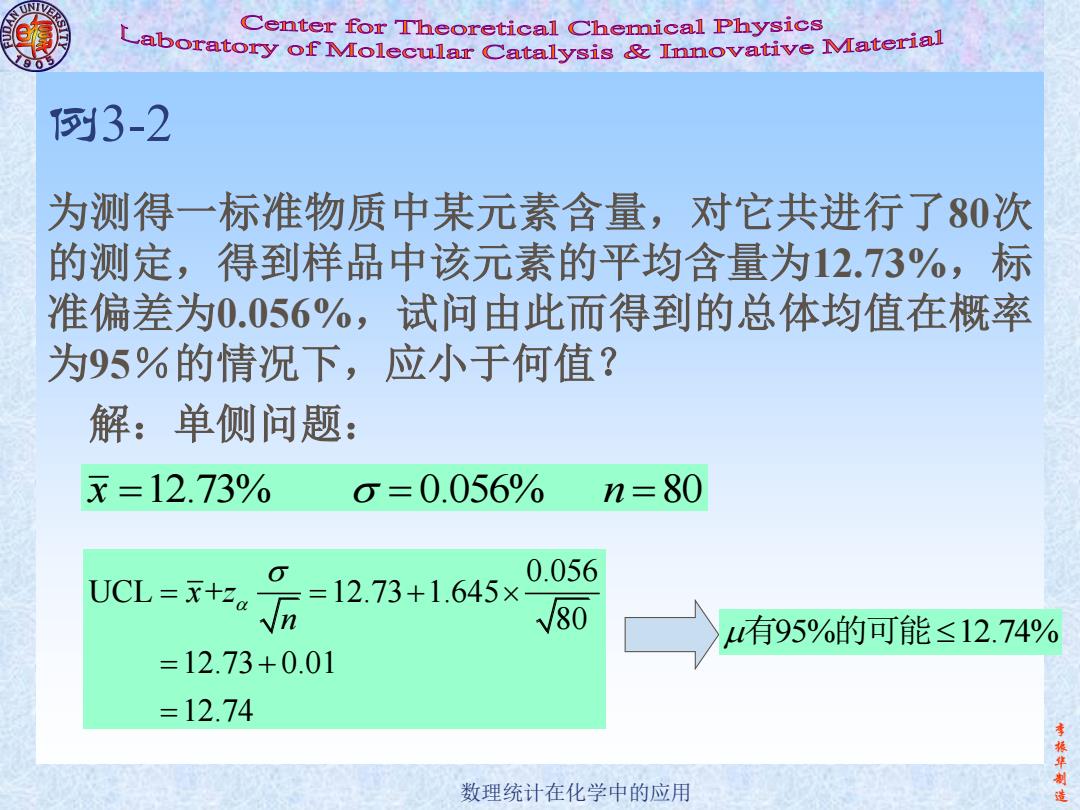
李 振 华 制 数理统计在化学中的应用 造 例3-2 为测得一标准物质中某元素含量,对它共进行了80次 的测定,得到样品中该元素的平均含量为12.73%,标 准偏差为0.056%,试问由此而得到的总体均值在概率 为95%的情况下,应小于何值? 解:单侧问题: 0.056 UCL + 12.73 1.645 80 12.73 0.01 12.74 x z n x n 12.73% 0.056% 80 有95% 12.74% 的可能
Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material (1)正态克体u的置信区间(σ未和) 只有在大样本时,>20 f(x) 0.4 ,才可以近似地用S来代替 口,此时只能用分布来求山 得置信区间 双侧问题: 0.241-a LCL=X-ta/2. S n UCL=x+ta/2.y S n 单侧问题: LCL=X-la. S UCL=X+la. S n n 振华制 数理统计在化学中的应用
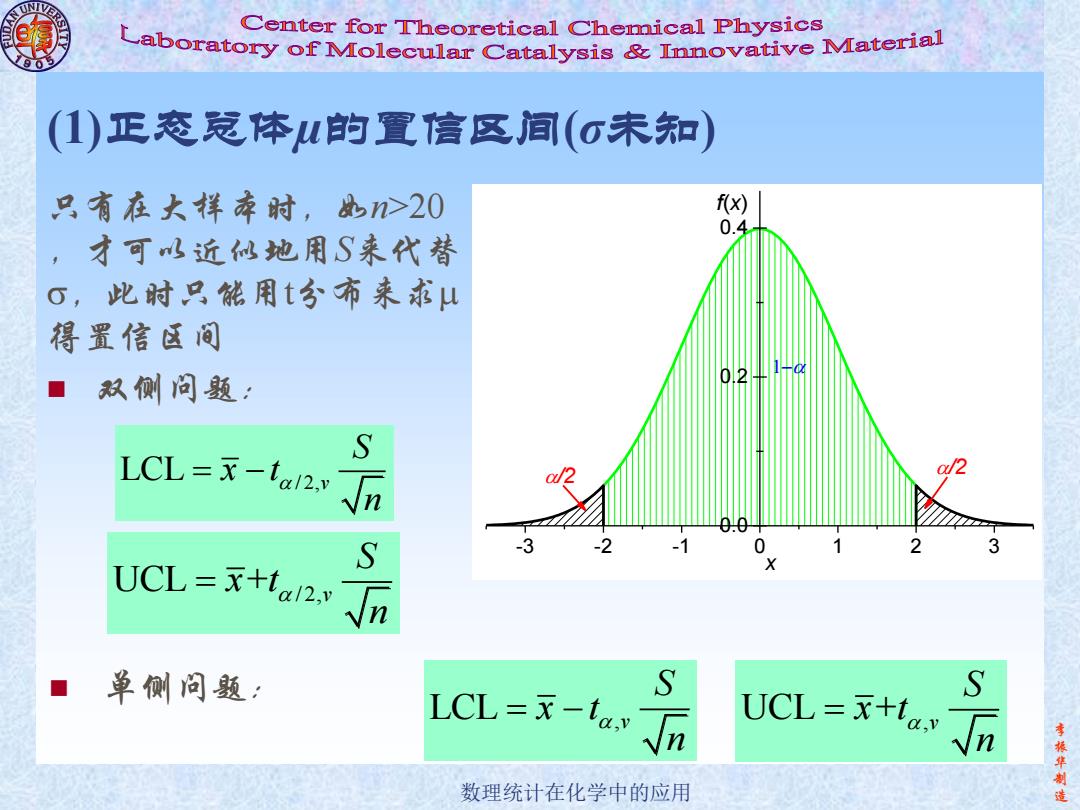
李 振 华 制 数理统计在化学中的应用 造 (1)正态总体µ的置信区间(σ未知) 只有在大样本时,如n>20 ,才可以近似地用S来代替 ,此时只能用t分布来求 得置信区间 双侧问题: LCL / 2,v S x t n -3 -2 -1 0 1 2 3 0.0 0.2 0.4 /2 /2 x f(x) UCL + / 2,v S x t n 单侧问题: UCL + ,v S x t n LCL ,v S x t n

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis Innovative Material 例3-21 为测得一标准物质中某元素含量,对它共进行了80次 的测定,得到样品中该元素的平均含量为12.73%,样 本标准偏差为0.056%,试问由此而得到的总体均值在 概率为95%的情况下,应小于何值? 解:单侧问题: x=12.73% S=0.056% n=80 0.056 UCL=x+ua.y =12.73+1.664× n √80 有95%的可能≤12.74% =12.73+0.01 =12.74 李振华制 数理统计在化学中的应用
李 振 华 制 数理统计在化学中的应用 造 例3-2’ 为测得一标准物质中某元素含量,对它共进行了80次 的测定,得到样品中该元素的平均含量为12.73%,样 本标准偏差为0.056%,试问由此而得到的总体均值在 概率为95%的情况下,应小于何值? 解:单侧问题: , 0.056 UCL + 12.73 1.664 80 12.73 0.01 12.74 v S x u n x S n 12.73% 0.056% 80 有95% 12.74% 的可能

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis&lnovative Material 例3-3 为检查某湖泊中鱼受污染情况,捕得鱼龄相近 的9条鱼,测得胸肌中汞含量(微克/克)如下 :1.85、1.86、1.93、2.01、2.03、2.05、2.07、 2.16、2.15,试求鱼胸肌中汞含量的99%置信 区间(假定汞含量服从正态分布)。 x=2.01 S=0.11 .005.8=3.355 UCL=2.01+3.355×0.11/V9=2.14 LCL=2.01-3.355×0.11/√9=1.89 李 振华制 数理统计在化学中的应用
李 振 华 制 数理统计在化学中的应用 造 例3-3 为检查某湖泊中鱼受污染情况,捕得鱼龄相近 的9条鱼,测得胸肌中汞含量(微克/克)如下 :1.85、1.86、1.93、2.01、2.03、2.05、2.07、 2.16、2.15 ,试求鱼胸肌中汞含量的99%置信 区间(假定汞含量服从正态分布)。 UCL 2.01+3.355 0.11/ 9=2.14 0.005,8 x S t 2.01 0.11 3.355 LCL 2.01 3.355 0.11/ 9=1.89