
设 E(x,y)=f(x)8(y) 代入方程和边界条件,得到 f"(x)+kf(x)=0 g"(y)+kg(y)=0 f(0)=0,f(a=0 k2+k=k足 8(0)=0,g(b)=0 其解分别为 m元 n元 ky= m=1,2,3,… a b (x)=Asin(x) mit a ()=Csin() n元 n=1,2,3,… 72元 n元 故 E.)(()E.sin(a )sin() a 2-2+2=(P+()- 截止波数只与波导 的结构尺寸有关。 K
设 E (x, y) f (x)g(y) z = 代入方程和边界条件,得到 = = + = (0) 0, ( ) 0 ( ) ( ) 0 2 f f a f x k f x x 2 ( ) ( ) 0 (0) 0, ( ) 0 y g y k g y g g b + = = = 2 2 2 x y c k k k + = π π ( ) sin( ) x m m k a m f x A x a = = π π ( ) sin( ) y n n k b n g y C y b = = m =1 2 3, ,, n =1 2 3, ,, 其解分别为 2 2 2 2 2 c π π ( ) ( ) mn xm yn m n k k k a b = + = + 故 π π ( , ) ( ) ( ) sin( )sin( ) zmn m n mn m n E x y f x g y E x y a b = = 截止波数只与波导 的结构尺寸有关

TM波的场分布 En(x)=Exe=5 sin)sin(答火 1m兀 En(xy,2)=- fk-mm m元 nπ Ox a 6E n元 m元 E3mn(x,y,)= jk:m oy in)cox(答e b Hs(x,y,2) jocd正m Jos nn k2 b .)co(答g m兀 n元 "cmn Hxm(x,y,2)=- Jos mn n元 n元 Ox co)sin(分e H-m(x,y,2)=0 m=1,2,3,·· n=1,2,32
2 2 mn cmn cmn 2 2 mn cmn cmn 2 2 mn cmn c π π π ( , , ) cos( )sin( )e π π π ( , , ) sin( )cos( )e j j π π ( , , ) sin( )cos zmn zmn zmn zmn zmn jk z xmn zmn zmn zmn jk z ymn znm xmn jk E jk m m n E x y z E x y k x k a a b jk E jk n m n E x y z E x y k y k b a b E n m H x y z E x k y k b a − − = − = − = − = − = = 2 2 mn cmn cmn π ( )e j j π π π ( , , ) cos( )sin( )e ( , , ) 0 zmn zmn jk z zmn jk z ymn zmn n y b E m m n H x y z E x y k x k a a b H x y z − − = − = − = TM波的场分布 mn π π ( , , ) ( , )e sin( )sin( )e zmn zmn jk z jk z znm zmn m n E x y z E x y E x y a b − − = = m =1 2 3, ,, n =1 2 3,
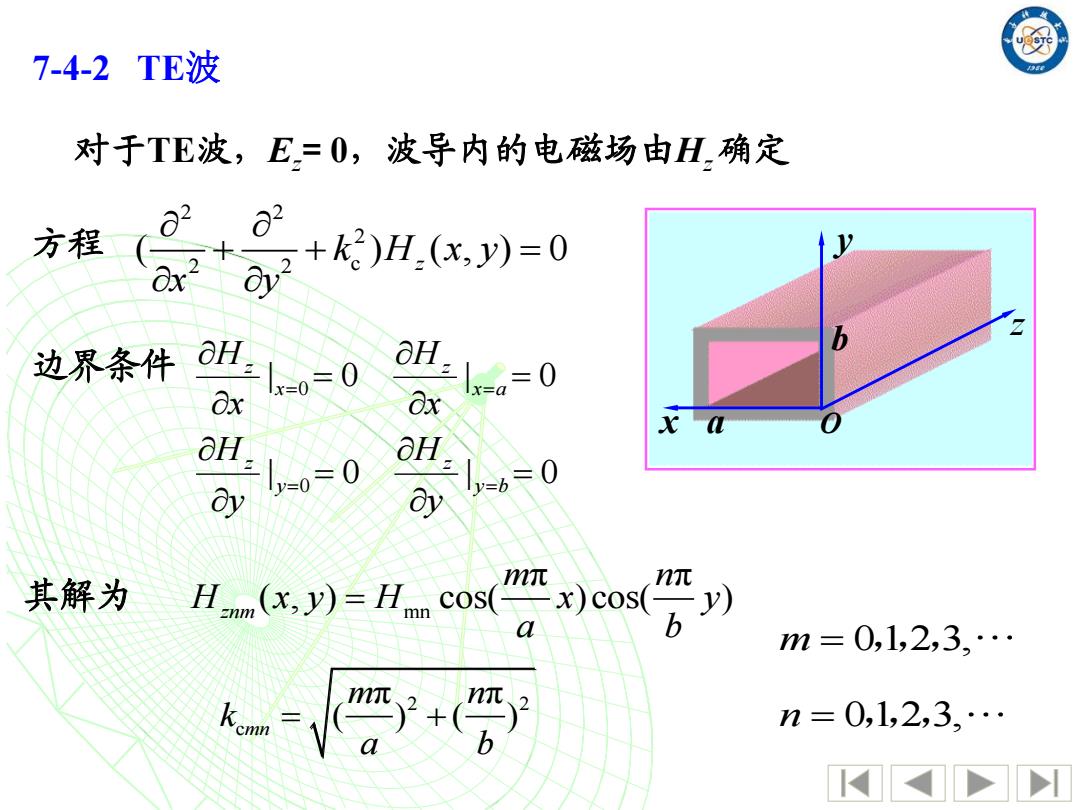
例 7-4-2TE波 对于TE波,E=0,波导内的电磁场由H,确定 方程 E+k)H,x川-0 边界条件 lx-0=0 Is-a=0 x a OH 1-0=0 1y6=0 其解为 H.月-H.cos0co(分y mπ m=0,1,2,3,… n=0,1,2,3,…
对于TE波,Ez = 0,波导内的电磁场由Hz 确定 7-4-2 TE波 2 2 2 2 2 c ( ) ( , ) 0 z k H x y x y + + = 方程 其解为 mn π π ( , ) cos( )cos( ) znm m n H x y H x y a b = 2 2 c π π ( ) ( ) mn m n k a b = + m = 0 1 2 3, ,,, n = 0 1 2 3, ,,, | 0 | 0 | 0 | 0 0 0 = = = = = = = = y b z y z x a z x z y H y H x H x 边界条件 H x y z O b a

TE波的场分布 H(xy)=Hcos(cos(ge m元 n兀 Hkg)-nyco(5e a jkm」 丑eosx小sin m元 n Hm(x,y,)= k2 b cmn Ew(x,y,2)= eg丑co()sin(答水 m元 n元 b a Eym(x,y,2)=- 匹coye 04业m n元 Em(x,y,2)=0 m=0,1,2,3,·n=0,1,2,3,… I
mn π π ( , , ) cos( )cos( )e zmn jk z zmn m n H x y z H x y a b − = 2 mn cmn 2 mn cmn 2 mn cmn 2 mn cmn π π π ( , , ) sin( )cos( )e π π π ( , , ) cos( )sin( )e j π π π ( , , ) cos( )sin( )e j π π ( , , ) sin( )cos( zmn zmn zmn zmn jk z xmn zmn jk z ymn jk z xmn ymn jk m m n H x y z H x y k a a b jk n m n H x y z H x y k b a b n m n E x y z H x y k b a b m m E x y z H x k a a − − − = = = = − π )e ( , , ) 0 zmn jk z zmn n y b E x y z − = m = 0 1 2 3, ,,, n = 0 1 2 3, ,,, TE波的场分布

7-4-3模式特性 m和n有不同的取值,对于m和n的每一种组合都有相应的 截波数kmm和场分布,即一种可能的模式,称为TMmm模或 TEmm模; 不同的模式有不同的截止波数k。m; 由于对相同的m和n,TMmn模和TEmn模的截止波数kcmm相 同,这种情况称为模式的简并; 对于TEm模,其m和n可以为0,但不能同时为0;而对于 TMmn模,其m和n不能为0,即不存在TMw模和TMon模
7-4-3 模式特性 m 和n 有不同的取值,对于m 和n 的每一种组合都有相应的 截波数kcmn和场分布,即一种可能的模式,称为TMmn模或 TEmn模; 不同的模式有不同的截止波数kcmn ; 由于对相同的m 和n,TMmn模和TEmn模的截止波数kcmn相 同, 这种情况称为模式的简并; 对于TEmn模,其m 和n可以为0,但不能同时为0;而对于 TMmn模, 其m 和n不能为0,即不存在TMm0模和TM0n模