
二、对函数形式的进一步讨论 ,1、关于对数函数形式的深入讨论 首先,我们回忆一下如何解释模型 log(price)=B+B log(nox)+B:rooms +u (6.6) 中的参数,其中变量都取自例4.5。记住,全书的log(x)都表示x的自然对数。系数B就是price 对o.xr(污染)的弹性。系数A是在△rooms=1时log(pric)的变化;就像我们多次看到的那样, 把它乘以100就近似等于价格变化的百分数。记得100·B有时也被称为price对roos的半弹性。 当使用HPRICE2中的数据进行估计时,我们得到 log (price)=9.23-0.718log(nox)+0.306rooms (0.19)(0.066) (0.019) (6.7) n=506,R=0.514 因此,当nox提高1%时,price在保持roos不变的情况下会下降0.718%。当rooms增加1时, price会提高近100X0.306=30.6%。 这个应用研究最终表明,增加一个房间会使价格提高约30.6%,这多少有些不太准确。因为随 着1og(y)变得越来越大,%△y≈100·△log(y)的近似就会越来越不准确,所以就出现了近似误 差。幸运的是,使用一种简单的运算就能计算出精确的百分比变化。 >I1 中级计量经济学
二、对函数形式的进一步讨论 1、关于对数函数形式的深入讨论 11 中级计量经济学

二、对函数形式的进一步讨论 ,利用对数函数形式优缺点: 优点: 1. 可用于计算弹性 2. 由于斜率系数不随测度单位变化而变化,所以可以忽略 以对数形式出现的变量的度量单位, 3. 以Ogy)作为因变量通常比使用y作为因变量更接近CLM假 定 4. 缩小变量的取值范围(对于取值为大额数值的变量,缓解异常值 对系数估计的影响) 》缺点 I. 当变量的取值在0至|之间时,取对数值后为负;变量取0 和负值 2. 更难预测原变量的值 12 中级计量经济学
利用对数函数形式优缺点: 优点: 1. 可用于计算弹性 2. 由于斜率系数不随测度单位变化而变化,所以可以忽略 以对数形式出现的变量的度量单位, 3. 以log(y)作为因变量通常比使用y作为因变量更接近CLM假 定 4. 缩小变量的取值范围(对于取值为大额数值的变量,缓解异常值 对系数估计的影响) 缺点: 1. 当变量的取值在0至1之间时,取对数值后为负;变量取0 和负值 2. 更难预测原变量的值 二、对函数形式的进一步讨论 12 中级计量经济学

二、对函数形式的进 一步讨论 2、含二次式的模型 在应用经济学中,为描述递减或递增的边际效应,常常用 到二次函数。或随Y随X非线性的变化关系。 在最简单的情形中,y只取决于一个单独可观测因素x,但又取决于其二次形式: y=R十3x+Ax2十u 比如,取y=uage和x=expr。如我们在第3章所讨论的那样,这个模型算不上简单回归分析, 但又很容易用多元回归来处理。 重要的是要记住,B并没有度量y相对x的变化;保持x不变而改变x是毫无意义的。如果我 们将估计方程写成 y=B十Bx十32x (6.10) 那么,我们就有如下近似: y对X的影响取决于X的取值 △夕≈(3十2Bx)△x,所以△/△r≈3十23x (6.11) 这说明,x和y之间的斜率取决于x的值;所估计的斜率是十23x。如果我们代入x=0,就会看 到,3可被解释为从x=0到x=1的近似斜率。此外,都必须考虑第二项23x。 如果我们只对给定x的起始值及其变化时计算y的预计变化量感兴趣,我们就可以直接使用 (6.10):完全没有理由去使用微积分做近似计算。但我们通常对概括x对y的影响更感兴趣,那么 方程(6.11)中对3和的解释就为我们提供了这种概括。通常,我们可以代入样本中x的平均 值,或某些有意义的数值,比如中位数或上下四分位点 >1 中级计量经济学
二、对函数形式的进一步讨论 2、含二次式的模型 在应用经济学中,为描述递减或递增的边际效应,常常用 到二次函数。或随Y随X非线性的变化关系。 13 中级计量经济学 y对x的影响取决于x的取值
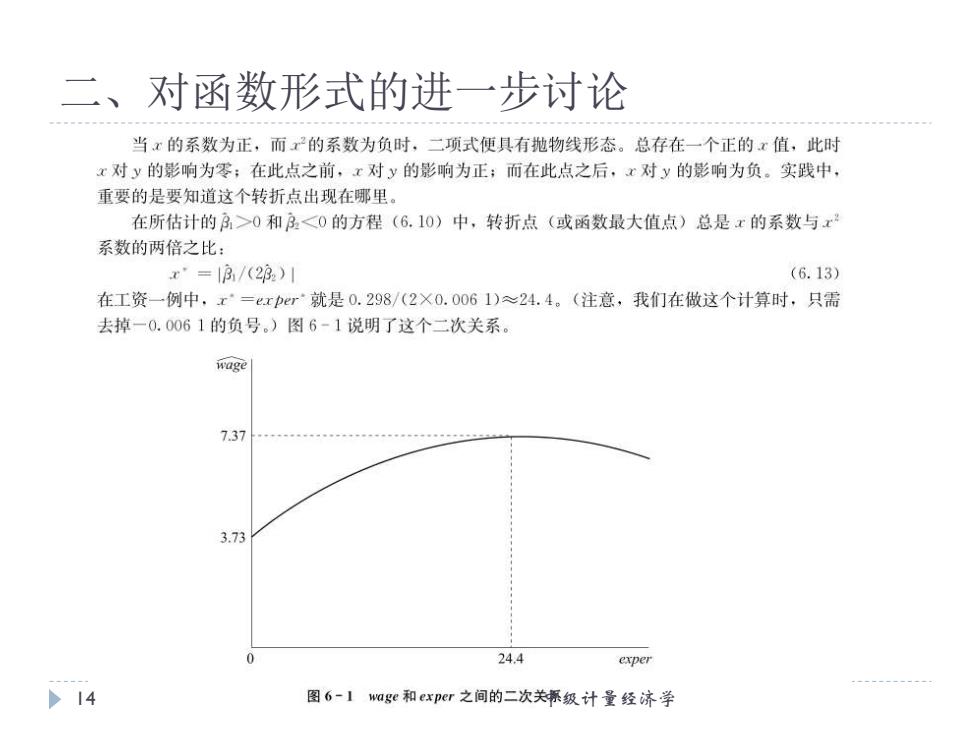
二、对函数形式的进一步讨论 当x的系数为正,而产的系数为负时,二项式便具有抛物线形态。总存在一个正的x值,此时 x对y的影响为零;在此点之前,x对y的影响为正;而在此点之后,x对y的影响为负。实践中, 重要的是要知道这个转折点出现在哪里。 在所估计的月>0和3<0的方程(6.10)中,转折点(或函数最大值点)总是x的系数与x 系数的两倍之比: x·=13/(28)1 (6.13) 在工资一例中,x=exper就是0.298/(2×0.0061)≈24.4。(注意,我们在做这个计算时,只需 去掉一0.0061的负号。)图6-1说明了这个二次关系。 wage 7.37 3.73 24.4 exper >14 图6-1wage和exper之间的二次关抓级计量经济学
二、对函数形式的进一步讨论 14 中级计量经济学

二、对函数形式的进 一步讨论 例子6.2 例6.2 污染对住房价格的影响 我们通过在例4.5中包括r00ms的二次项而修改住房价格模型: log(price)=B+月log(ox)+log(dist)+Amos +B:rooms'+Bstratio +u (6.14) 利用HPRICE2中的数据估计上述模型,得到 log(price)=13.39-0.902log(noxr)-0.087log(dist) (0.57) (0.115) (0.043) -0.545roo1s+0.062 rooms2-0.048s1rati0 (0.165)(0.013)(0.006) n=506,R2=0.603 二次项roo1s2的t统计量约为4.77,所以它在统计上是相当显著的。但解释roos对log(price)的影响会怎 么样呢?起初,其影响看起来有些奇怪。由于rO0s的系数为负,而ro0s的系数为正,所以这个方程确实 意味着,在roos的值很低时,增加一个房间对log(price)具有负影响。到某个点后,开始变为正影响,这 个二次项的形态意味着,price对ooms的半弹性随着ooms的增加而递增。这种情况示于图6-2。 15 中级计量经济学
例子6.2 二、对函数形式的进一步讨论 15 中级计量经济学