
线性规划问题的数学模型 例1.9将线性规划问题化为标准型 Min f-3x+5x,+8x3-7x st.2x1-3x2+5x3+6x4≤28 4x1+2x2+3x3-9x4≥39 6x2+2x3+3x4≤-58 X1,x3,x4≥0;x2无约束 解: Maxz=3x,-5x2+5x2”-8x3+7x4 s.t2x3x2'+3x2”+5x3+6x4+x=28 4x十2x2’-2x2"”+3x3-9x4x=39 -6x2+6x2”-2x33x4x7=58 X1x2'x2,3x4x5,x6,x7≥0
例1.9 将线性规划问题化为标准型 解: Min f= -3 x1 + 5 x2 + 8 x3 - 7 x4 s.t. 2 x1 - 3 x2 + 5 x3 + 6 x4 ≤ 28 4 x1 + 2 x2 + 3 x3 - 9 x4 ≥ 39 6 x2 + 2 x3 + 3 x4 ≤ - 58 x1 , x3 , x4 ≥ 0; x2无约束 Max z = 3x1 –5x2 ’+5x2 ”–8x3 +7x4 s.t. 2x1 –3x2 ’+3x2 ”+5x3 +6x4 +x5 = 28 4x1 +2x2 ’-2x2 ”+3x3 -9x4 -x6 = 39 -6x2 ’+6x2 ”-2x3 -3x4 -x7 = 58 x1 ,x2 ’,x2 ”,x3 ,x4 ,x5 ,x6 ,x7 ≥ 0 线性规划问题的数学模型
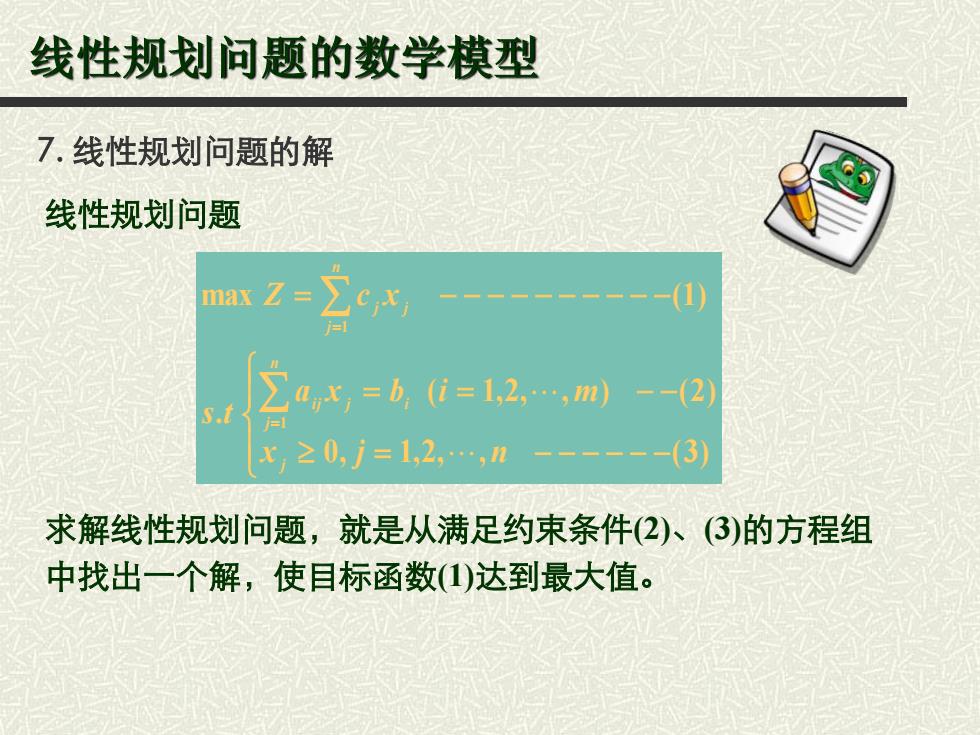
线性规划问题的数学模型 7.线性规划问题的解 线性规划问题 max Z= -2 5.t ∑a=b0=12,m x20,=12,n (3 求解线性规划问题,就是从满足约束条件(2)(3)的方程组 中找出一个解,使目标函数(1)达到最大值
线性规划问题的数学模型 7. 线性规划问题的解 0, 1,2, , (3) ( 1,2, , ) (2) . max (1) 1 1 x j n a x b i m s t Z c x j n j i j j i n j j j 线性规划问题 求解线性规划问题,就是从满足约束条件(2)、(3)的方程组 中找出一个解,使目标函数(1)达到最大值

线性规划问题的数学模型 ·可行解:满足约束条件②、③的解为可行解。所有可行解 的集合为可行域。 最优解:使目标函数达到最大值的可行解。 ·基:设A为约束条件②的m×n阶系数矩阵(m<n),其秩为m, B是矩阵A中m阶满秩子矩阵(|B|0),称B是规划问题的 个基。设: 1m B= =(p.pn) 称B中每个列向量P,(j=12·.例为基向量。与基向量P 对应的变量x,为基变量。除基变量以外的变量为非基变量
线性规划问题的数学模型 • 可行解:满足约束条件②、③的解为可行解。所有可行解 的集合为可行域。 • 最优解:使目标函数达到最大值的可行解。 • 基:设A为约束条件②的m×n阶系数矩阵(m<n),其秩为m, B是矩阵A中m阶满秩子矩阵(∣B∣≠0),称B是规划问题的 一个基。设: ( ) 1 1 1 1 1 m m mm m p p a a a a B 称 B中每个列向量Pj ( j = 1 2 . . m) 为基向量。与基向量Pj 对应的变量xj 为基变量。除基变量以外的变量为非基变量

线性规划问题的数学模型 ·基解:某一确定的基B,令非基变量等于零,由约束条件 方程②解出基变量,称这组解为基解。在基解中变量取非0 值的个数不大于方程数m,基解的总数不超过Cm ·基可行解:满足变量非负约束条件的基本解,简称基可行 解。 ·可行基:对应于基可行解的基称为可行基。 可行解 基解 非可行解 基可行解
线性规划问题的数学模型 • 基解:某一确定的基B,令非基变量等于零,由约束条件 方程②解出基变量,称这组解为基解。在基解中变量取非0 值的个数不大于方程数m,基解的总数不超过 • 基可行解:满足变量非负约束条件的基本解,简称基可行 解。 • 可行基:对应于基可行解的基称为可行基。 m C n 非可行解 可 行 解 基解 基可行解

线性规划问题的数学模型 例1.4求线性规划问题的所有基、基解、基可行解和最优解 maxZ=2x1+3x2+0x3+0x4+0x5 2x1+2x2+X3=12 4x1+x4=16 5x2+X5=15 x≥0,j=1,.,5
线性规划问题的数学模型 例1.4 求线性规划问题的所有基、基解、基可行解和最优解 0, 1, ,5 5 15 4 16 2 2 12 max 2 3 0 0 0 2 5 1 4 1 2 3 1 2 3 4 5 x j x x x x x x x Z x x x x x j