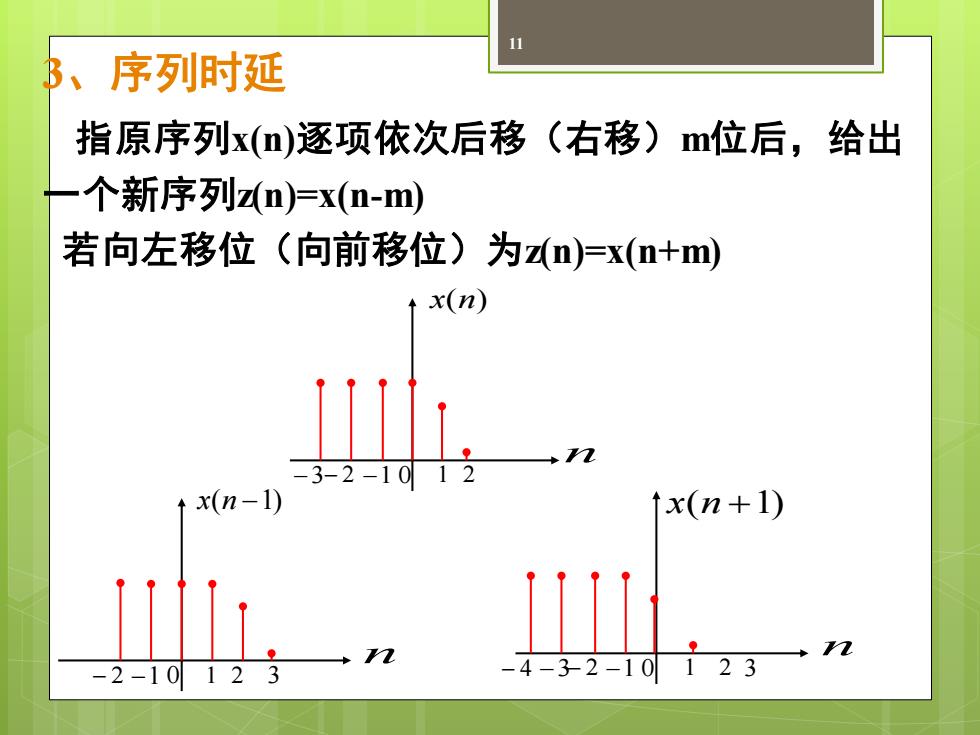
11 3、序列时延 指原序列x(n)逐项依次后移(右移)位后,给出 一个新序列n)=x(n-m) 若向左移位(向前移位)为n)=x(n+m) +x(n) I. -3-2-1012 x(n-1) ↑x(n+1) -2-10123 -4-32-10 123→ n
11 3、序列时延 指原序列x(n)逐项依次后移(右移)m位后,给出 一个新序列z(n)=x(n-m) 若向左移位(向前移位)为z(n)=x(n+m) n −3− 2 −1 0 1 2 x(n) n x(n −1) − 2 −1 0 1 2 3 n x(n +1) − 4 −3− 2 −1 0 1 2 3
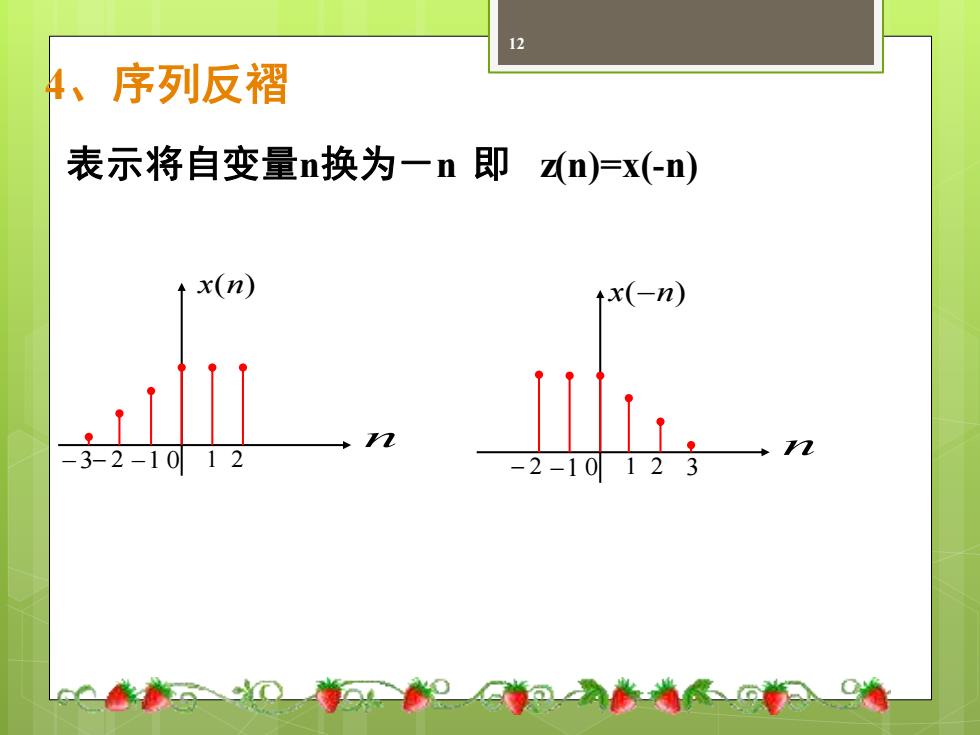
12 4、序列反褶 表示将自变量n换为一n即zn)=x(n) tx(n) x(-n) 32-1012 -2-1012 一0-0把和》-49
12 4、序列反褶 表示将自变量n换为-n 即 z(n)=x(-n) n x(n) −3− 2 −1 0 1 2 n x(−n) − 2 −1 0 1 2 3

13 5、尺度变换 将波形压缩或扩展,这时要按规律去处某些点 或补足相应的零点值,这种运算又称序列重排。 若将自变量n乘以正数a,构成x(an)为压缩。 而x()则为波形的扩展。 a
13 5、尺度变换 将波形压缩或扩展,这时要按规律去处某些点 或补足相应的零点值,这种运算又称序列重排。 而 则为波形的扩展。 若将自变量n乘以正整数 构 成 为压缩。 ) a n x( a, x(an)
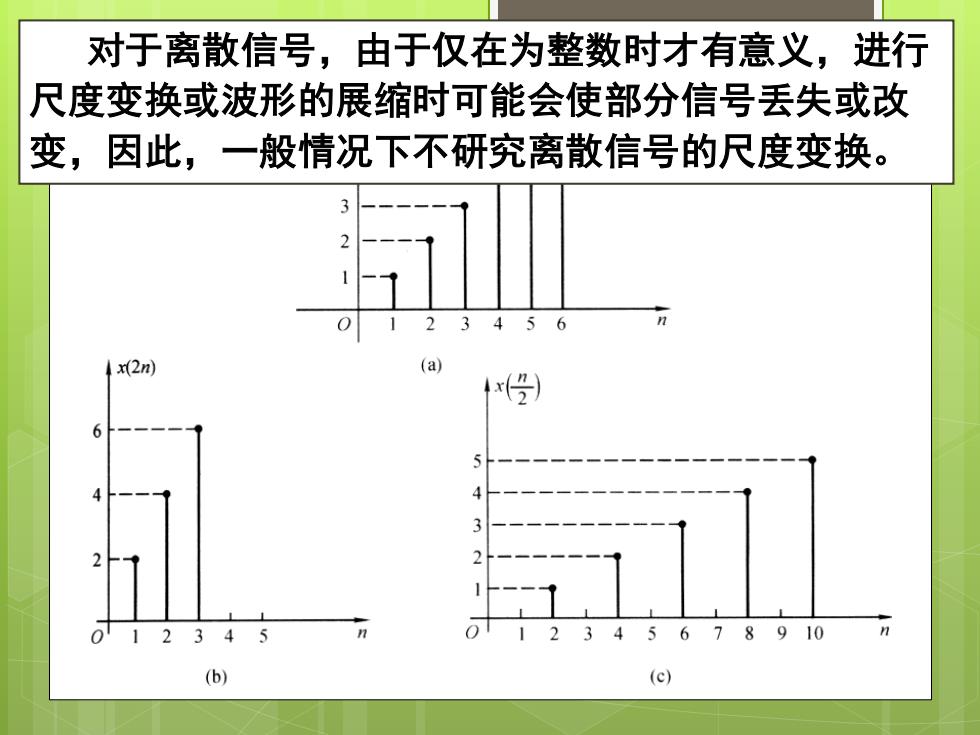
对于离散信号,由于仅在为整数时才有意义,进行 尺度变换或波形的展缩时可能会使部分信号丢失或改 变,因此,一般情况下不研究离散信号的尺度变换。 3 4x2m) (a 4x( 234 78910 (b) (c)
对于离散信号,由于仅在为整数时才有意义,进行 14 尺度变换或波形的展缩时可能会使部分信号丢失或改 变,因此,一般情况下不研究离散信号的尺度变换

15 6、 序列差分(对应于连续信号的微分) 十阶前向差分 △x(n)=x(n+1)-x(n) 土阶前向差分 △[△x(n]=A'x(n)=△x(n+1)-△x(n =x(n+2)-2x(n+1)+x(n 阶后向差分 Vx(n)=x(n)-x(n-1) 二阶后向差分 [x(n]=72x(n)=Vx(n)-Vx(n-1) =x(n-2x(n-1)+x(n-2)
15 6、序列差分(对应于连续信号的微分) 一阶前向差分 二阶前向差分 一阶后向差分 x(n) = x(n +1) − x(n) ( ) ( ) ( 1) ( ) 2 x n = x n = x n + − x n = x(n + 2) − 2x(n +1) + x(n) x(n) = x(n) − x(n −1) 二阶后向差分 ( ) 2 ( 1) ( 2) ( ) ( ) ( ) ( 1) 2 = − − + − = = − − x n x n x n x n x n x n x n