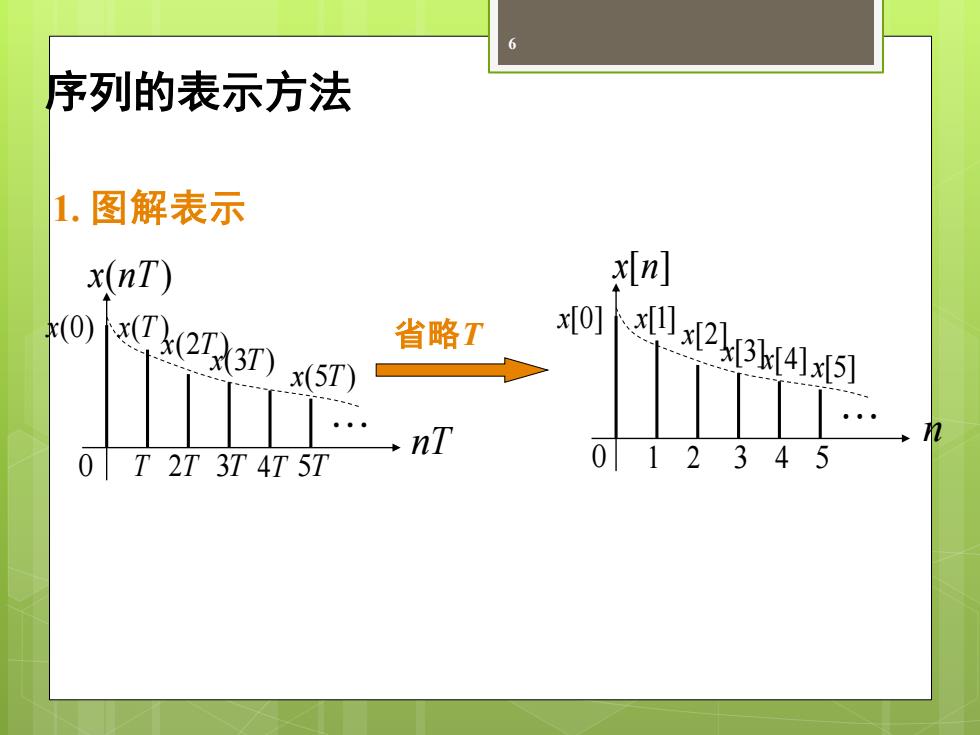
序列的表示方法 1.图解表示 x(nT) x(n] O) 省略T x[0] 5T) 0234 .nT . 0 T 2T 3T 4T 5T 012345
6 x nT ( ) x(0) x(T ) x(2T ) x(3T) x(5T) nT T 2T 3T 4T 5T 0 x n[ ] x[0] x[1] x[2]x[3] x[5] n 1 2 3 4 5 0 x[4] 省略T 1. 图解表示 序列的表示方法
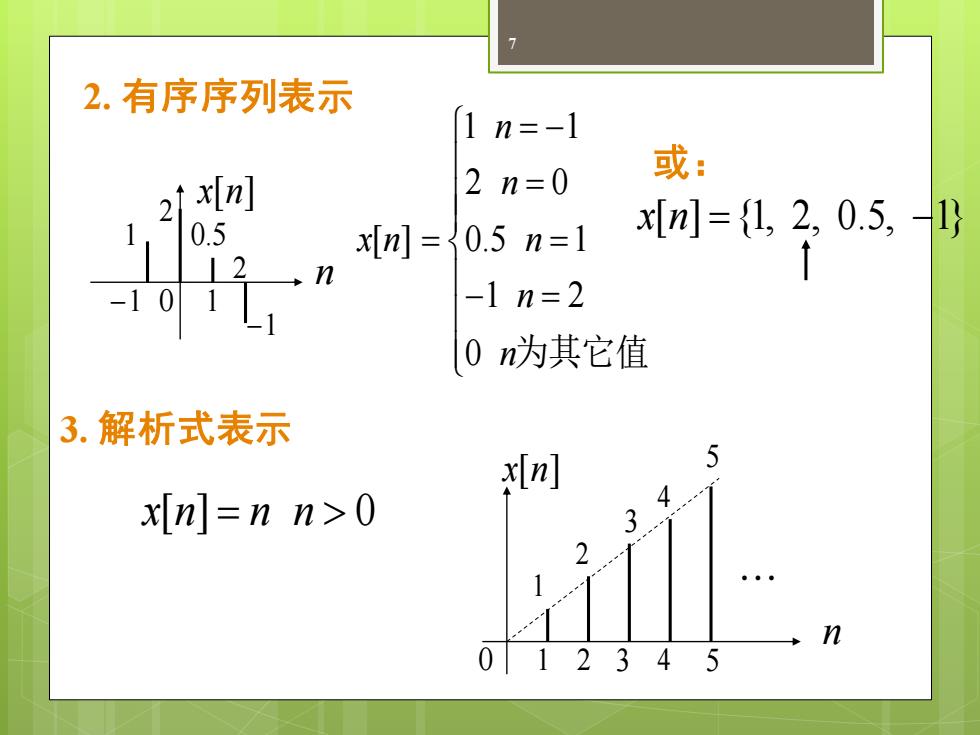
2.有序序列表示 1n=-1 2n=0 或: 21 xln] 0.5 x[n]=0.5n=1 x[n={L,2,0.5,1 -1n=2 0n为其它值 3.解析式表示 *In] 5 xn=nn>O 41 3 2 1 n 0 12345
7 2. 有序序列表示 1 1 2 0 [ ] 0.5 1 1 2 0 n n x n n n n = − = = = − = 为其它值 x n[ ] {1, 2, 0.5, 1} = − 或: −1 0 1 2 n x n[ ] 2 1 −1 0.5 3. 解析式表示 x n n n [ ] 0 = x n[ ] n 1 2 3 4 5 0 5 4 3 2 1

二、序列的分类 1.双边序列 序列x(n)对所有的整数n(-oo<<co)都存在确定的非零值。 2.单边序列 有始序列(右边序列):当n≤n,时,x(n)=0 n,≥0的有始序列称为因果例 有终序列(左边序列):当n≥n,时,x(n)=0 3.有限序列 n,≤0的有终序列称为反因黥列 序列x(n汉在n1≤n≤n,区间有非零确定值
8 二、 序列的分类 1. 双边序列 序列 x (n) 对所有的整数 n (-<n<)都存在确定的非零值。 2. 单边序列 有始序列(右边序列): 当n n1 时,x(n) = 0 有终序列(左边序列): n2 0的有终序列称为反因果序 列 3. 有限序列 n1 0的有始序列称为因果序列

三、离散信号的一些基本运算 1.序列相加 序列x(m)与y(m相加,是指两个序列同序号的数 值逐项相应相加,而构成一个新的序列z,即 z(n)=x(n)+y(n) 2.序列相乘 序列x(m)与yn相乘,是指两个序列同序号的数值 逐项相应相乘,而构成一个新的序列z),即: z(n)=x(n).y(n)
9 三、离散信号的一些基本运算 1. 序列相加 序列x(n) 与y(n)相加,是指两个序列同序号的数 值逐项相应相加,而构成一个新的序列z(n) ,即 z(n) = x(n) + y(n) z(n) = x(n) y(n) 2. 序列相乘 序列x(n) 与y(n)相乘,是指两个序列同序号的数值 逐项相应相乘,而构成一个新的序列z(n) ,即:

0 xm)= n<-1 2 2m+5n≥-1 x2(n)= n+2 n≥0 0 n<-1 2"” n<-1 n=-1 x2(n)= n=-1 2-m+5n≥0 n+2 n≥0 2” n<-1 x(n)+x2(n)= 153 n=-1 2"+n+7 n≥0 0 n<-1 x (n)x2(n)= 75 n=-1 n2"+2"+1+5n+10 n≥0
10 + = − − = − 2 5 0 7 1 0 1 ( ) 1 n n n x n n 解: + = − − = 2 0 1 2 1 2 1 ( ) 2 n n n n x n n + + = − − + = − 2 7 0 1 2 15 2 1 ( ) ( ) 1 2 n n n n x n x n n n + + + = − − = − − + 2 2 5 10 0 1 2 7 0 1 ( ) ( ) 1 1 2 n n n n n x n x n n n + − − = − 2 5 1 0 1 ( ) 1 n n x n n + = 2 0 2 0 ( ) 2 n n n x n n