第7章通信信道与无线链路 表711各种调制方式在香农容量限速率时的误码特性 带 R=C时比特误码特性P-E,/N。 102 103103106 调制 调制 率 进制 方式 CIW E E (bps/Hz) N N M=2 BPSK 1 0(dB) 0.075 4.30 6.77 9.56 10.5 QPSK 1.76 0.045430 6.779.56 10.5 M- MOWM 0.0981 4.36 678 956 10.5 MPSK 3.68 0.051 7.33 10.05 12.99 13.96 MPAM 3.68 012661203 14g1770 1878 MOWM 34 0414 0.103 3.8 5.85 828 9.14 MPSK 5.74 0.07311.54 14.4117.45 18.45 MPAM 5.74 01423 1654 1945 2151 2152 M=16 5.74 801 10.58 13.45 14.41 MAPSK 5.74 0.08311.01 13.5816.45 17.41 MOWM 0817 0.21563554 5237.409 821 MPSK 792 009011624 19262238 2339 MPAM 7.92 0.149221.35 24.3727.52 28.53 M=32 MAPSK 7.92 0.076 13.06 15.69 18.6 19.56 MOWM 5/16 027533163 745 10.2 0.028 12.21 14.92 18.83 M=64 MOWM 3/16 -145 0.349 2882 4.25 6.153 6.87 MOAM 0060710R2 266 M-256 MOWM 16 -1.50 0.4328 2.486 2.65 539 6.02 M=1024MOwM5256 -1.56 0.48092.255 326 4.781 5.37 M=8192MOWM13/4096 .1587 388 188 472 M=2 MOWM 32x2 -1.600 0.5-81.62 2.02 2.73 305 从图7-15、表1-1-1以及(7-1-12武,我们可以得到下述结论: ①当C/W=1时,E,/N。=1,即(OB);即频谱效率为1bps/Hz时,可靠通信(误码率 可任意小)所需要最低信噪比为0B。 ②当C/W→o时,E。/N。呈指数规律增长: 5成器导8-号 7-1-13) ③当C/W→0时 E,-.2-a-16 ⑦-114 E,/N。一1.6B被称为香农极限,它是能进行无误码传输的最低归一化信噪比值:但此时频谱 效率趋近于无穷小。 西安电子科技大学 6
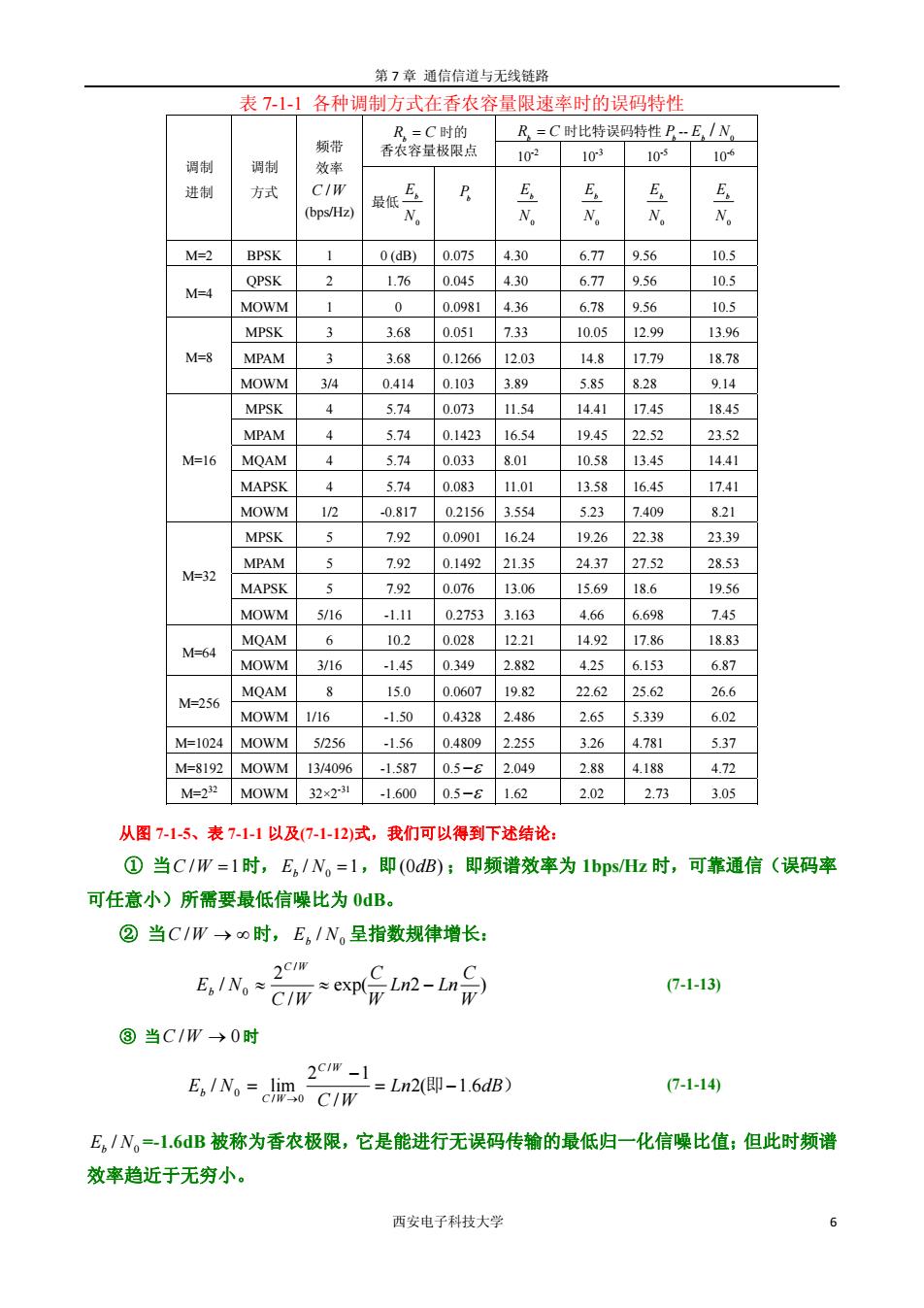
第 7 章 通信信道与无线链路 西安电子科技大学 6 表 7-1-1 各种调制方式在香农容量限速率时的误码特性 b R C= 时比特误码特性 b P - 0 / b E N b R C= 时的 香农容量极限点 10-2 10-3 10-5 10-6 调制 进制 调制 方式 频带 效率 C W/ (bps/Hz) 最低 0 Eb N b P 0 Eb N 0 Eb N 0 Eb N 0 Eb N M=2 BPSK 1 0 (dB) 0.075 4.30 6.77 9.56 10.5 QPSK 2 1.76 0.045 4.30 6.77 9.56 10.5 M=4 MOWM 1 0 0.0981 4.36 6.78 9.56 10.5 MPSK 3 3.68 0.051 7.33 10.05 12.99 13.96 M=8 MPAM 3 3.68 0.1266 12.03 14.8 17.79 18.78 MOWM 3/4 0.414 0.103 3.89 5.85 8.28 9.14 MPSK 4 5.74 0.073 11.54 14.41 17.45 18.45 MPAM 4 5.74 0.1423 16.54 19.45 22.52 23.52 MQAM 4 5.74 0.033 8.01 10.58 13.45 14.41 MAPSK 4 5.74 0.083 11.01 13.58 16.45 17.41 M=16 MOWM 1/2 -0.817 0.2156 3.554 5.23 7.409 8.21 MPSK 5 7.92 0.0901 16.24 19.26 22.38 23.39 MPAM 5 7.92 0.1492 21.35 24.37 27.52 28.53 MAPSK 5 7.92 0.076 13.06 15.69 18.6 19.56 M=32 MOWM 5/16 -1.11 0.2753 3.163 4.66 6.698 7.45 MQAM 6 10.2 0.028 12.21 14.92 17.86 18.83 M=64 MOWM 3/16 -1.45 0.349 2.882 4.25 6.153 6.87 MQAM 8 15.0 0.0607 19.82 22.62 25.62 26.6 M=256 MOWM 1/16 -1.50 0.4328 2.486 2.65 5.339 6.02 M=1024 MOWM 5/256 -1.56 0.4809 2.255 3.26 4.781 5.37 M=8192 MOWM 13/4096 -1.587 0.5 −ε 2.049 2.88 4.188 4.72 M=232 MOWM 32×2-31 -1.600 0.5 −ε 1.62 2.02 2.73 3.05 从图 7-1-5、表 7-1-1 以及(7-1-12)式,我们可以得到下述结论: ① 当C W/ 1 = 时, 0 / 1 E N b = ,即(0 ) dB ;即频谱效率为 1bps/Hz 时,可靠通信(误码率 可任意小)所需要最低信噪比为 0dB。 ② 当C /W → ∞ 时, 0 Eb / N 呈指数规律增长: exp( 2 ) / 2 / / 0 W C Ln Ln W C C W E N C W b ≈ ≈ − (7-1-13) ③ 当C /W → 0时 Ln 即 dB) C W E N C W C W b 2( 1.6 / 2 1 / lim / / 0 0 = − − = → (7-1-14) 0 / Eb N =-1.6dB 被称为香农极限,它是能进行无误码传输的最低归一化信噪比值;但此时频谱 效率趋近于无穷小

第7章通信信道与无线链路 ④图中香农限容量限曲线上的任一点,对应于以纵坐标所指频带效率进行无误码传输时 所需的最低信噪比E。/N。(横坐标),或以横坐标所指E,/N。值进行无误码传输时最高可能达 到的频带效率。例如:CW=3bp/H时,最低信噪比为73(约为3.68dB);当E。/N。=10B时,最高频 带效率约为5.877bs/Hz。同香农功率限一样,实现无误码传输只能无限逼近这条曲线所表示的容量极限。 ⑤在105误码率下,常用的各种调制方式都与相同频带效率下的香农信噪比极限有很大 的差距;如BPSK所需信噪比为9.6dB,而相同频带效率下的香农信噪比极限为0B,相差9.6dB:缩小 这种差距的主要方法就是进行信道编码。 ⑥任意一种调制方式当向左靠近香农容量限曲线时其误码率越来越高,但一直到曲线上 时其误码率一般还是显著低于50%;这说明超出香农容量限并不是完全不能进行通信,而只是不能 以波形信道方式进行无误码的通信。 7.1.3各种波形信道的容量及其逼近香农限的方法 ·构成波形信道的主要因素就是数字调制,不同调制方式所构成的波形信道具有不同的信 道容量和不同的误码特性。要使一种波形信道实现其信道容量,即逼近香农极限容量, 一般都需要通过信道编码才能实现。 ·数据传输特性逼近香农限有两层含义: ①传输速率接近香农容量限,追求频带效率; ②在给定速率下使所需E,/N。逼近香农容量限的最低值;追求功率效率。 ·香农容量限曲线的两个伸展方向,分别对应于高频带效率区和高功率效率区,这两个区都 有许多特殊的应用:中间区域是频带效率和功率效率折中的情况,常规通信系统应用最多。 任何一种波形信道,总是可以结合信道编码而逼近香农限:其依据是下面的定理。 【有噪信道编码定理】在一个信道容量为C的信道中传输信息速率为R的数字信息,如 果R<C,则总存在一种信道编码方法能使传输信息的差错率任意小;而若R>C,则不可能找 到一种信道编码方法使信息传输差错率趋于0。 这个定理表明,任何一种调制方式都可以采用码率略小于1的无穷长码的编码方法,使 它在以小于香农容量限的速率传输时能做到无误码传输。 基于M进制数字调制的波形信道,其归一化信道容量应该是: C/W=(Log,M0/W-△(bps (7-115) 这里△值的大小与调制方式有关,其值应该显著小于C/W。其所以存在这个差距△,是因为 采用码率等于1的任何一种信道编码方法都不具有足够大的编码增益,能使信道在以凡/W的 西安电子科技大学
第 7 章 通信信道与无线链路 西安电子科技大学 7 ④ 图中香农限容量限曲线上的任一点,对应于以纵坐标所指频带效率进行无误码传输时 所需的最低信噪比 0 / E N b (横坐标),或以横坐标所指 0 / E N b 值进行无误码传输时最高可能达 到的频带效率。例如:C/W=3bp/Hz 时,最低信噪比为 7/3(约为 3.68dB);当 0 / E N b =10dB 时,最高频 带效率约为 5.877bps/Hz。同香农功率限一样,实现无误码传输只能无限逼近这条曲线所表示的容量极限。 ⑤ 在 10-5 误码率下,常用的各种调制方式都与相同频带效率下的香农信噪比极限有很大 的差距;如 BPSK 所需信噪比为 9.6dB,而相同频带效率下的香农信噪比极限为 0dB,相差 9.6dB;缩小 这种差距的主要方法就是进行信道编码。 ⑥ 任意一种调制方式当向左靠近香农容量限曲线时其误码率越来越高,但一直到曲线上 时其误码率一般还是显著低于 50%;这说明超出香农容量限并不是完全不能进行通信,而只是不能 以波形信道方式进行无误码的通信。 7.1.3 各种波形信道的容量及其逼近香农限的方法 z 构成波形信道的主要因素就是数字调制,不同调制方式所构成的波形信道具有不同的信 道容量和不同的误码特性。要使一种波形信道实现其信道容量,即逼近香农极限容量, 一般都需要通过信道编码才能实现。 z 数据传输特性逼近香农限有两层含义: ① 传输速率接近香农容量限,追求频带效率; ② 在给定速率下使所需 0 / E N b 逼近香农容量限的最低值;追求功率效率。 z 香农容量限曲线的两个伸展方向,分别对应于高频带效率区和高功率效率区,这两个区都 有许多特殊的应用;中间区域是频带效率和功率效率折中的情况,常规通信系统应用最多。 任何一种波形信道,总是可以结合信道编码而逼近香农限;其依据是下面的定理。 【有噪信道编码定理】在一个信道容量为 C 的信道中传输信息速率为 R 的数字信息,如 果 R<C,则总存在一种信道编码方法能使传输信息的差错率任意小;而若 R>C,则不可能找 到一种信道编码方法使信息传输差错率趋于 0。 这个定理表明,任何一种调制方式都可以采用码率略小于 1 的无穷长码的编码方法,使 它在以小于香农容量限的速率传输时能做到无误码传输。 基于 M 进制数字调制的波形信道,其归一化信道容量应该是: C W/ = 2 ( )/ Log M W − Δ (bps) (7-1-15) 这里Δ值的大小与调制方式有关,其值应该显著小于C W/ 。其所以存在这个差距Δ,是因为 采用码率等于 1 的任何一种信道编码方法都不具有足够大的编码增益,能使信道在以 / Rb W 的

第7章通信信道与无线链路 归一化速率传输信息时的误码率降低到儿乎等于0。 表7-1-1中还提供了图7-1-5中102和10两种误码率情况下各种调制方式所需E。/N。值,以及10 和10两种误码率情况下各种调制方式所需E,/N。值。这些数据是选用逼近香农限的实际信道编码方法的 重要依据或参考:一般数据传输的误比特率要求为10°左右,而采用码率较高(接近于1)的有限长码的信道 编码方法,要想能获得较高的编码增益,一般需要译码器输入数据的误比特率小于102103。表中MOWM 表示M进制正交波形调制, 表7.1列出的各种调制方式在以香农容量限的速率传输信息时的误码特性,都是基于相干解调、理 想成形滤波器的情况。其中M进制正交波形调制MOWM),例如M元扩频,其频带效率计算公式和比特 误码表达式,在第5章中已经推导, 逼近香农限的数据传输,除了信道编码方法的讲究之外,调制方式的选择也是十分重要的:表7山 中提供的数据也是调制方式选择的重要参考。 结合信道编码逼近香农容量限的方法有多种,主要有以下三类: ()基于高效信道编码通近香农容量限 采用如Tubo码、LDPC码等编码增益很高、译码门限较低的信道编码方法,对于各种调 制方式的输入数据进行编码,对输出的软判决量进行译码,就可以有效地逼近香农容量限:一般采用适当 长的码,码率在78时即可使比特误码率降低到10,而E,/N。只比香农容量限处的值高1-2dB。 (②)采用M进制正交波形调制通近香农限 从图7-15和表7-11可以看出,M进制正交波形调制随着M的增大而逐渐逼近香农限, 因为它本质上就是一种随机码信道编码与数字调制相结合的产物;它是在高功率效率区通近香农 限的,不过逼近过程的比较缓慢:真正接近香农极限信噪比E,/N。一16B,所需的M值非常大。 如果将M进制正交波形调制再与某种基于代数码(如Tubo码、LDPC码等)的信道编码方 法相结合,则可以显著改善它逼近香农限的程度。 ()基于编码调制方法逼近香农容量限 将信道编码与数字调制融合在一起,使码间的汉明距离与信号矢量间的欧氏距离有更好 的对应关系,即构成编码调制系统,可以使系统以更有效地逼近香农限,例如TCM编码调 制就是很好的例子。 7.1.4信道可靠性函数E(R) 无限带宽AWGN信道的信道可靠性函数定义为 [C./2-R(0≤R≤C./4) E(R)= (,-R2 (C /4sRsC) (7-1-16) 西安电子科技大学
第 7 章 通信信道与无线链路 西安电子科技大学 8 归一化速率传输信息时的误码率降低到几乎等于 0。 表 7-1-1 中还提供了图 7-1-5 中 10-2 和 10-5 两种误码率情况下各种调制方式所需 0 / E N b 值,以及 10-3 和 10-6 两种误码率情况下各种调制方式所需 0 / E N b 值。这些数据是选用逼近香农限的实际信道编码方法的 重要依据或参考;一般数据传输的误比特率要求为 10-6 左右,而采用码率较高(接近于 1)的有限长码的信道 编码方法,要想能获得较高的编码增益,一般需要译码器输入数据的误比特率小于 10-2~10-3。表中 MOWM 表示 M 进制正交波形调制。 表 7-1-1 列出的各种调制方式在以香农容量限的速率传输信息时的误码特性,都是基于相干解调、理 想成形滤波器的情况。其中 M 进制正交波形调制(MOWM),例如 M 元扩频,其频带效率计算公式和比特 误码表达式,在第 5 章中已经推导。 逼近香农限的数据传输,除了信道编码方法的讲究之外,调制方式的选择也是十分重要的;表 7-1-1 中提供的数据也是调制方式选择的重要参考。 结合信道编码逼近香农容量限的方法有多种,主要有以下三类: (1) 基于高效信道编码逼近香农容量限 采用如 Turbo 码、LDPC 码等编码增益很高、译码门限较低的信道编码方法,对于各种调 制方式的输入数据进行编码,对输出的软判决量进行译码,就可以有效地逼近香农容量限;一般采用适当 长的码,码率在 7/8 时即可使比特误码率降低到 10-6,而 0 / E N b 只比香农容量限处的值高 1~2dB。 (2) 采用 M 进制正交波形调制逼近香农限 从图 7-1-5 和表 7-1-1 可以看出,M 进制正交波形调制随着 M 的增大而逐渐逼近香农限, 因为它本质上就是一种随机码信道编码与数字调制相结合的产物;它是在高功率效率区逼近香农 限的,不过逼近过程的比较缓慢;真正接近香农极限信噪比 0 / E N b =-1.6dB,所需的 M 值非常大。 如果将 M 进制正交波形调制再与某种基于代数码(如 Turbo 码、LDPC 码等)的信道编码方 法相结合,则可以显著改善它逼近香农限的程度。 (3) 基于编码调制方法逼近香农容量限 将信道编码与数字调制融合在一起,使码间的汉明距离与信号矢量间的欧氏距离有更好 的对应关系,即构成编码调制系统,可以使系统以更有效地逼近香农限,例如 TCM 编码调 制就是很好的例子。 7.1.4 信道可靠性函数E( ) R 无限带宽 AWGN 信道的信道可靠性函数定义为 2 / 2 (0 / 4) ( ) ( ) ( /4 ) C R RC E R C R C RC ∞ ∞ ∞ ∞ ∞ ⎧ − ≤≤ ⎪ = ⎨ ⎪ − ≤≤ ⎩ (7-1-16)