拉压③全应力分解为:★垂直于截面的应力称为“正应力”(Normal Stress) ;ANdNTD0=1limdAAOAA福MO★位于截面内的应力称为“剪应力”(Shearing Stress)。AQ_ do-lmwu
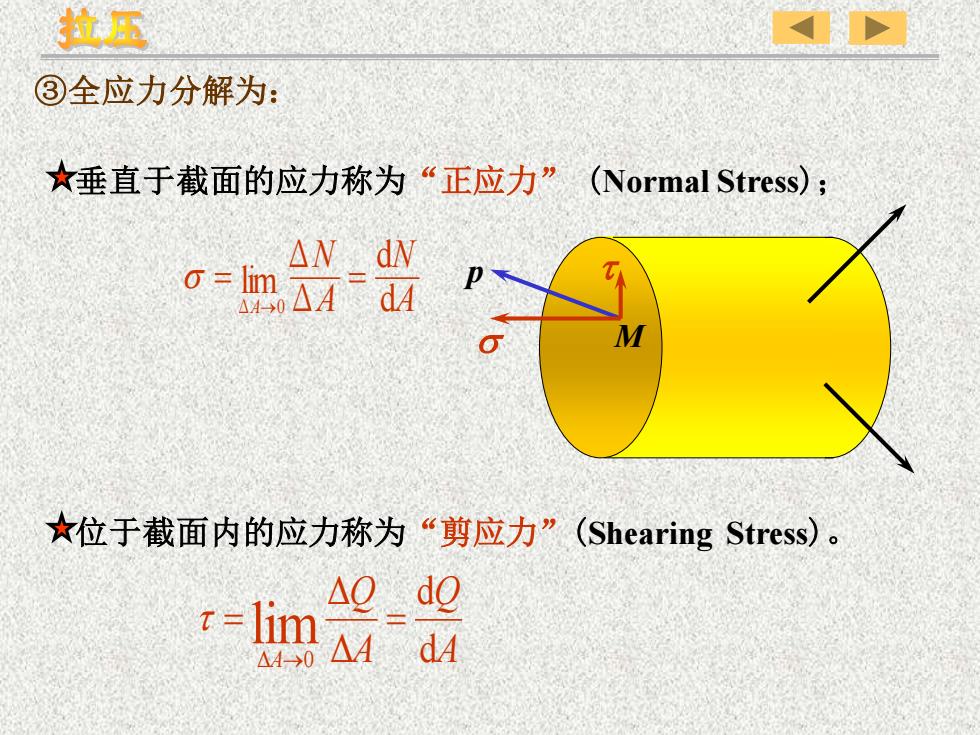
③全应力分解为: p M A N A N A d d Δ Δ lim Δ 0 = = → A Q A Q A d d Δ Δ lim Δ 0 = = → 垂直于截面的应力称为“正应力” (Normal Stress); 位于截面内的应力称为“剪应力”(Shearing Stress)
拉压拉(压)杆横截面上的应力1.变形规律试验及平面假设:横截面6a变形前dCba受载后dC平面假设:原为平面的横截面在变形后仍为平面。纵向纤维变形相同
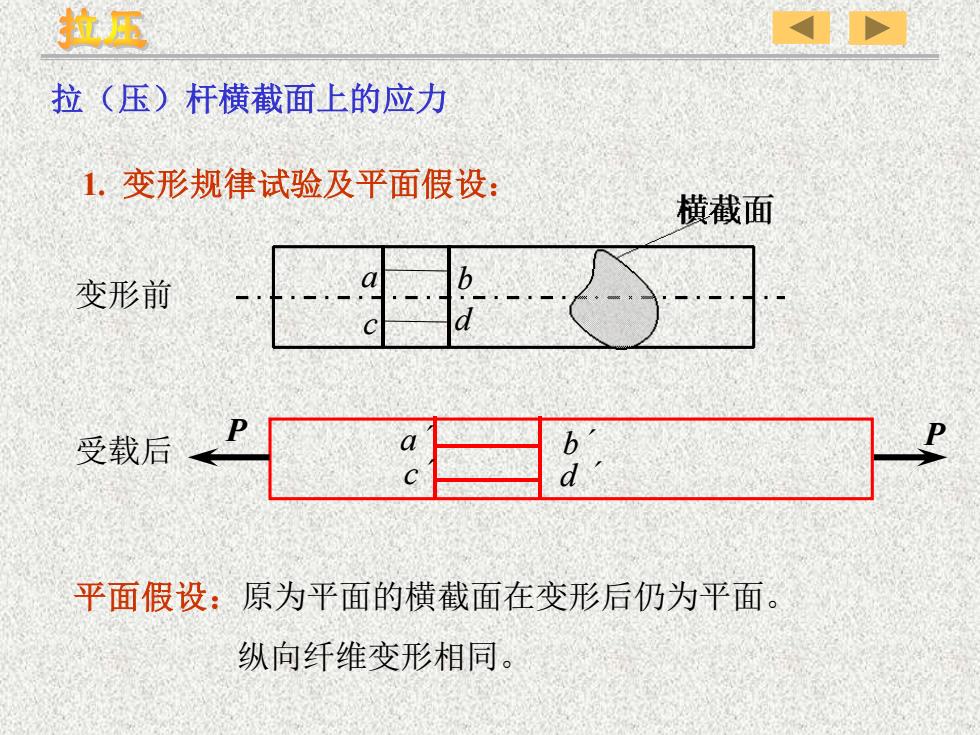
变形前 1. 变形规律试验及平面假设: 平面假设:原为平面的横截面在变形后仍为平面。 纵向纤维变形相同。 a b c d 受载后 P P d ´ a´ c´ b´ 拉(压)杆横截面上的应力

拉压均匀材料、均匀变形,应力当然均匀分布。2.拉伸应力:N(x)9:N(x)PA轴力引起的正应力一α:在横截面上均布。3.危险截面及最大工作应力:危险截面:内力最大的面,截面尺寸最小的面。危险点:应力最大的点。N(x)o=maxOmaxA(x)
均匀材料、均匀变形,应力当然均匀分布。 2. 拉伸应力: N(x) P A N(x) = 轴力引起的正应力 —— : 在横截面上均布。 危险截面:内力最大的面,截面尺寸最小的面。 危险点:应力最大的点。 3. 危险截面及最大工作应力: ) ( ) ( ) max( max A x N x =

拉压4.公式的应用条件直杆、杆的截面无突变、截面到载荷作用点有一定的距离。5.圣维南原理离开载荷作用处一定距离,应力分布与大小不受外载荷作用方式的影响。P.aPPD
直杆、杆的截面无突变、截面到载荷作用点有一定 的距离。 4. 公式的应用条件: 5. 圣维南原理: 离开载荷作用处一定距离,应力分布与大小不受外载荷作 用方式的影响
拉压例4图示结构,试求杆件AB、CB的应力。已知F=20kN:斜杆AB为直径20mm的圆截面杆,水平杆CB为15×15的方截面杆。解:1、计算各杆件的轴力345°(设斜杆为1杆,水平杆为2杆)B用截面法取节点B为研究对象2-FFNI-ZF=0Fni COS 45° + FN2 = 0B45°FNXF sin 45°- F = 0ZF,=0FFMl = 28.3kNFv2 = -20kN
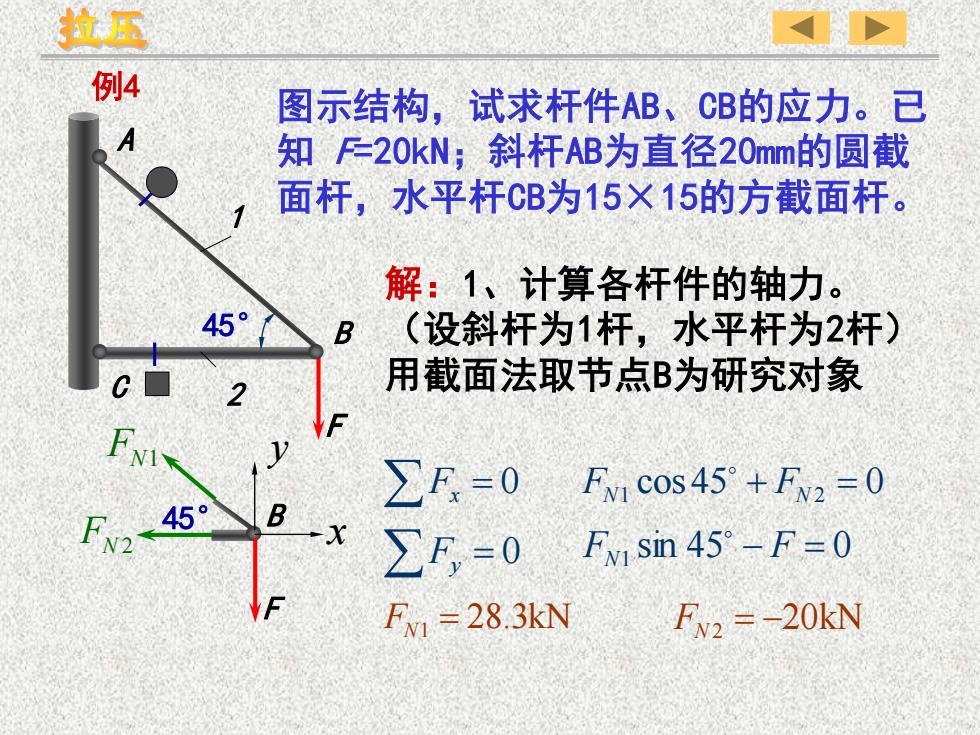
例4 图示结构,试求杆件AB、CB的应力。已 知 F=20kN;斜杆AB为直径20mm的圆截 面杆,水平杆CB为15×15的方截面杆。 F A B C Fy = 0 FN1 = 28.3kN 解:1、计算各杆件的轴力。 (设斜杆为1杆,水平杆为2杆) 用截面法取节点B为研究对象 FN2 = −20kN Fx = 0 45° FN1 cos 45 + FN 2 = 0 sin 45 0 FN1 − F = 1 2 F B F FN1 FN 2 x y 45°