
拉压[例21图示杆的A、B、C、D点分别作用着大小为5P、8P、4PP的力,方向如图,试画出杆的轴力图DBCOPDPPBDBCAPPPBP解:求OA段内力N:设置截面如图ZX=0 N -P +P-P-P,=0N -5P+8P-4P-P=0N. =2P
[例2] 图示杆的A、B、C、D点分别作用着大小为5P、8P、4P、 P 的力,方向如图,试画出杆的轴力图。 解: 求OA段内力N1:设置截面如图 A B C D PA PB PC PD O A B C D PA PB PC PD N1 X = 0 N1 − PA + PB − PC − PD = 0 N1 −5P +8P − 4P − P = 0 N1 = 2P

拉压DBCN2同理,求得AB、BC、CD段内力分PcPDPBD别为:CN3N2- -3PPDPcN3= 5PDNN4- PPD轴力图如右图5PN2P1PU3P
同理,求得AB 、 BC 、CD段内力分 别为: N2= – 3 P N3= 5 P N4= P 轴力图如右图 B C D PB P C PD N2 C D P C PD N3 DPD N4 N x 2 P 3 P 5 P+ P + –

拉压[例3]图示杆长为L,受分布力 q=kx 作用,方向如图,试画出杆的轴力图2解:x坐标向右为正,坐标原点在q(x)自由端。取左侧x 段为对象,内力N(x)为:q(x)qx2N(x)OXqLN(x)=16-kxdx=-kxNxOSkBN(x)max = -一kP2
解:x 坐标向右为正,坐标原点在 自由端。 取左侧x 段为对象,内力N(x)为: q qL x O 2 0 2 1 N(x) k xdx k x x = − = − 2 max 2 1 N(x) = − k L [例3] 图示杆长为L,受分布力 q = kx 作用,方向如图,试画出 杆的轴力图。 L q(x) N(x) x q(x) N x O – 2 2 kL

拉压S 6.2 轴向拉伸或压缩时横截面上的应力问题提出:pPpP1.内力大小不能衡量构件强度的大小。2.强度:①材料承受载荷的能力:②内力在截面分布集度一应力。应力概念的回顾1.定义:由外力引起的内力集度
问题提出: P P P P 1. 内力大小不能衡量构件强度的大小。 2. 强度:①材料承受载荷的能力; ②内力在截面分布集度⎯应力。 1. 定义:由外力引起的内力集度。 应力概念的回顾 §6.2 轴向拉伸或压缩时横截面上的应力
拉压工程构件,大多数情形下,内力并非均匀分布,集度的定义不仅准确而且重要,因为“破坏”或“失效”往往从内力集度最大处开始。2.应力的表示:MAP①平均应力:△PAAPmNA②全应力(总应力):△pdPlimp= IdA△A
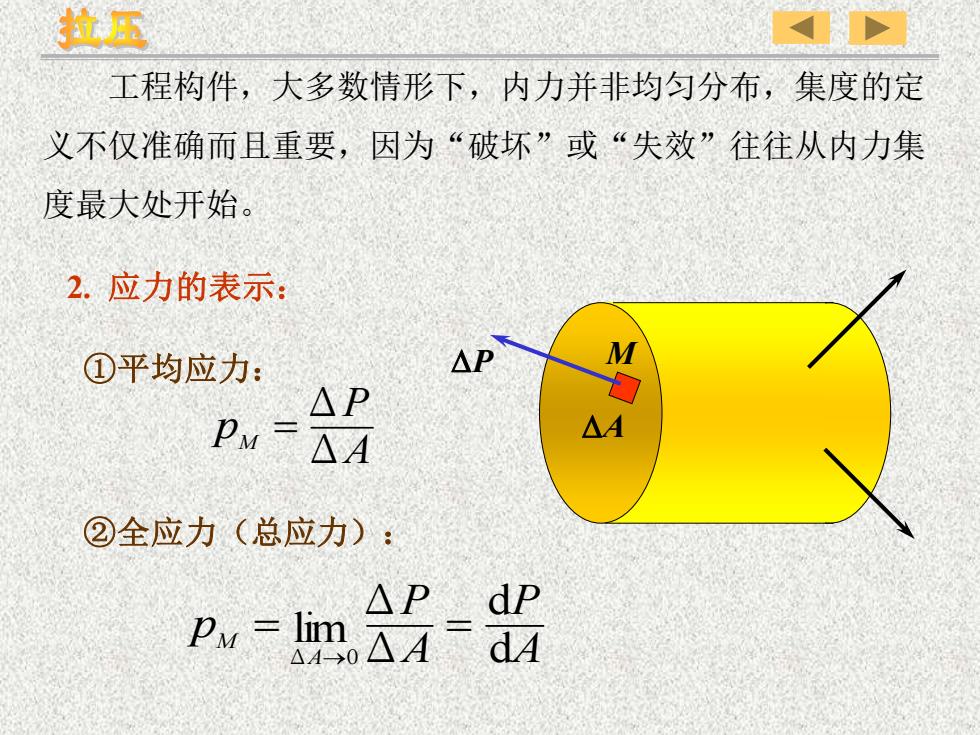
工程构件,大多数情形下,内力并非均匀分布,集度的定 义不仅准确而且重要,因为“破坏”或“失效”往往从内力集 度最大处开始。 P A ①平均应力: M ②全应力(总应力): A P pM Δ Δ = A P A P p A M d d Δ Δ lim Δ 0 = = → 2. 应力的表示: