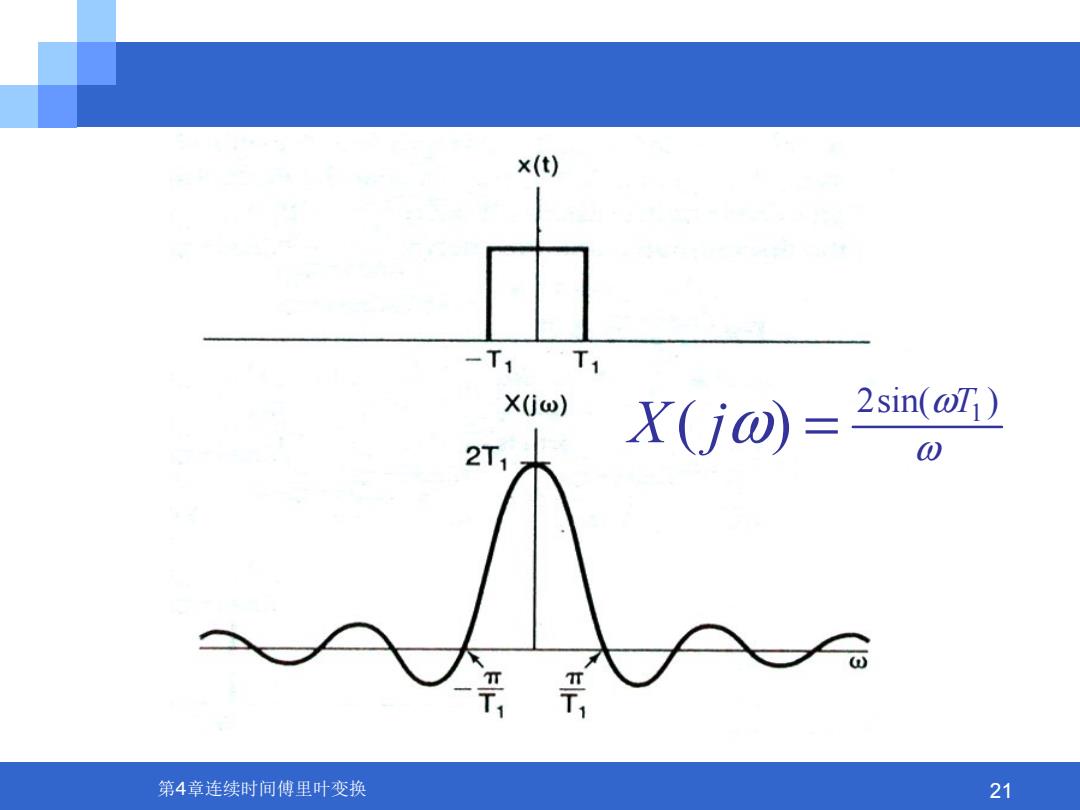
x(t) -T1T1 X0ω) X(jω)= 2sin(@) 2T1 0 第4章连续时间傅里叶变换 21
第4章连续时间傅里叶变换 21 ω ω ω 1 )sin(2 )( T jX =

4.1.2傅里叶变换的收敛 冬与傅里叶级数是否收敛所要求的那一组条件一样。 Dirichlet条件: 条件1:绝对可积 ∫Ix(u)ldh<o 条件2:单个周期内,x()的最大最小值的数 目有限 条件3:在任何有限区间内,X()有有限个不连续点,并且在 每个不连续,点都必须是有限值。 第4章连续时间傅里叶变换 22
第4章连续时间傅里叶变换 22 4.1.2傅里叶变换的收敛 与傅里叶级数是否收敛所要求的那一组条件一样。 Dirichlet 条件: 条件1:绝对可积 ∞< T |)(| dttx 条件2:单个周期内,x(t)的最大最小值的数 目有限 条件3:在任何有限区间内, x(t)有有限个不连续点,并且在 每个不连续点都必须是有限值

4.1.3连续时间傅里叶变换举例 例题4.1 4.2 4.3 4.44.5 第4章连续时间傅里叶变换 23
第4章连续时间傅里叶变换 23 例题 4.1 4.2 4.3 4.4 4.5 4.1.3 连续时间傅里叶变换举例

P207例题4.1 己知:x(t)=e(t) a>0 求:x(t)←7→X(j0)=? 作图 讨论,若: (0) a<0 (2) a=0 (3) a为复数:Re{a<0,或Re{a=0,或Re{a>0 X(U0=? 第4章连续时间傅里叶变换 24
第4章连续时间傅里叶变换 24 P207 例题 4.1 = > 0)()(: − atuetx 已知 at ←⎯→ jXtx ω = ?)()(: 求 FT a < 0)1( 讨论,若: a = 0)2( )3( a为复数 a < 或 a = 或 a > 0}Re{,0}Re{,0}Re{: jX ω = ?)( 作图

例4.1考虑信号 IX(jo)I x(t)=e“u(t}a>0 由(49式,有 1/a xi)d v2a/2 、、1 -e-(a+i): a jw 也就是 XGw)=、1 a+jo, a>0 -a a 这个博里叶变换是复数,要画出作为 山的函数,就需要利用它的模和相位 来表示X(w) 支Xo) π/2 文X5如)=-sn(g) /4 iX(jw)川和文X(Gm)如图4.5所示。 -a 注意,若a是复数而不是实数,那么 0 -4 只要观{a}>0,x(t)就是绝对可积 的,并且在这种情况下X(Gw)具有同 n/2 样的形式,即 X(jo)=-1 jw' %la}>0 图4.5例4.1中信号x(t)=e"u(t),a>0的傅里叶变换 例4.2母,11为