
P207例题4.2 己知:x(t)=ea4 a>0 求:x(t)←可→X(U0)=? 作图 讨论,若: (0) a<0 (2) a=0 (3) a为复数:Re{a<0,或Re{a=0,或Re{a>0 X(jo)=? 第4章连续时间傅里叶变换 26
第4章连续时间傅里叶变换 26 P207 例题 4.2 )(: >= 0 − aetx ta 已知 ←⎯→ jXtx ω = ?)()(: 求 FT a < 0)1( 讨论,若: a = 0)2( )3( a为复数 a < 或 a = 或 a > 0}Re{,0}Re{,0}Re{: jX ω = ?)( 作图
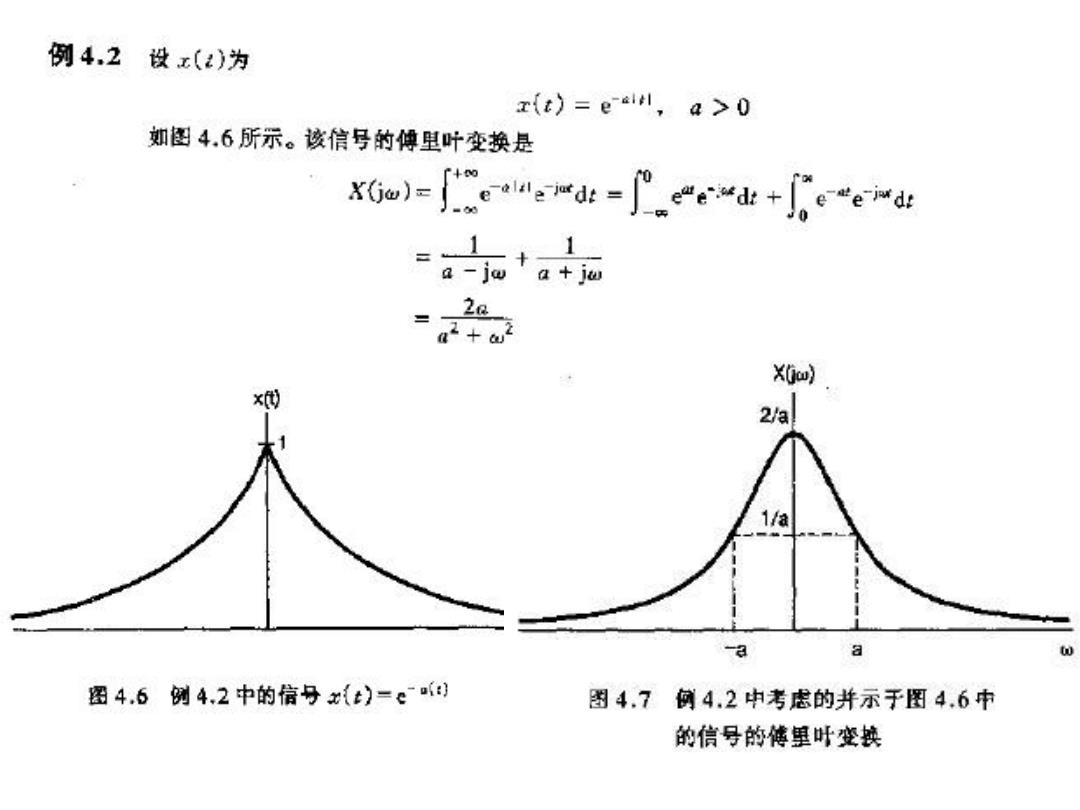
例4.2 设x()为 r(t)=esin,a>0 如图4.6所示。该信号的傅里叶变换是 x0o=d-j.c产e+ee a-jw 2 a2+ X(jc) ) 2/a 1/a -a 图4.6 例4,2中的信号x{t)=e) 图4.7何4.2中考虑的并示于图4.6中 的信号的傅里叶变换

P208令 例题4.3 已知:x(t)=6t) 求:x0←可→X(j)=? 作图 时域有限,频域无限 第4章连续时间傅里叶变换 28
第4章连续时间傅里叶变换 28 P208 例题 4.3 已知 =δ ttx )()(: ←⎯→ jXtx ω = ?)()(: 求 FT 作图 时域有限,频域无限

例4.3求单位冲激函数的傅里叶变换 x(t)=(t) 解: X(jo)=∫rx(t)edh =」rou)edt e-j@0 =1 这就是说,单位冲激函数的频谱在所有频率上都是 相同的
例4.3 求单位冲激函数的傅里叶变换 解: 这就是说,单位冲激函数的频谱在所有频率上都是 相同的。 x() () t t = δ 0 ( ) () ( ) 1 j t j t j X j x t e dt t e dt e ω ω ω ω δ +∞ − −∞ +∞ − −∞ − = = = =

P208例题4.4 已知:x0可 1,4<☑ 0,4>T 作图 求:x(t)←7→X(j0)=? 时域有限,频域无限 第4章连续时间傅里叶变换 30
第4章连续时间傅里叶变换 30 P208 例题 4.4 > < = 1 1 ,0 ,1 )(: Tt Tt 已知 tx ←⎯→ jXtx ω = ?)()(: 求 FT 作图 时域有限,频域无限