
十0 当T→∞, x(t0) T→x() (t)=∑aeka k T→0 k=-∞ 2rT-∞→d0 T d.=)e-Aavdr 因此 aT=∫x()edh=X(jw) x()=mm。∑a4etm, T∞ k=- = lim Σ X(jkω。) T→∞ k=- T 1im。∑X(koo)e*' 00 00→0 2π ∫X(jo)eodo 第4章连续时间傅里叶变换 16
第 4章连续时间傅里叶变换 16 当 T→∞ , ⎯⎯ →⎯ ωω T ∞→ k 0 因此 )( ω )( ω jXdtetxTa tj k = = +∞∞− − ∞+ ∞− ∞+ = −∞ → ∞+ = −∞ ∞→ +∞ = −∞ ∞→ = = = = ω ω π π ω ω ω ω ω ω ω ω dejX ejkX e T jkX tx ea tj k tjk k tjk T k tjk k T )( 2 1 2 lim )( )( lim lim)( 0 0 0 0 0 0 0 0 )()( ~ txtx ⎯T⎯ →⎯∞→ ω π ω d T 2 ⎯= T⎯ →⎯∞→ 0 0 0 ( ) 1 ( ) jk t k k jk t k T xt ae a x t e dt T ω ω + ∞ =−∞ − = =

()的傅里叶级数是 (t)=∑aew k=-o∞ a,0e- (t)ek'dt 由于在<T2内,(t)=x(t),而在其余地方x()=0, 所以有 a)ede 因此,定义Ta的包络Xjw)为 X(j)=x(t)e-jdi
的傅里叶级数是 由于在|t|<T/2内, ,而在其余地方x(t)=0, 所以有 因此,定义Tak的包络X(jω)为 x ( )t 0 0 0 / 2 / 2 ( ) 1 1 () () jk t k k T jk t jk t k T T xt ae a x t e dt x t e dt T T ω ω ω +∞ =−∞ − − − = = = x () () t xt = 0 0 / 2 / 2 1 11 () () () T jk t jk t j t k T a x t e dt x t e dt x t e dt T TT ω ω ω +∞ +∞ − − − − −∞ −∞ = == ( ) () j t X j x t e dt ω ω +∞ − −∞ =
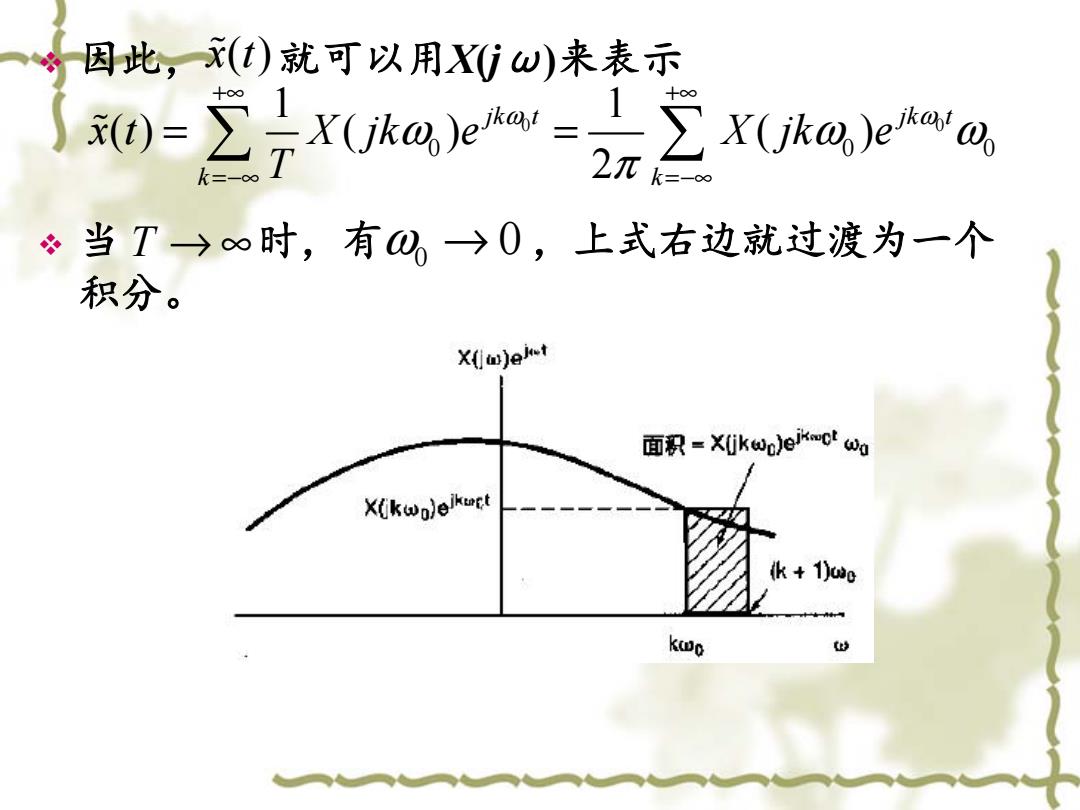
因此,(t)就可以用Xω)来表示 正网g=三a 一●● K=-00 必 当T→∞时,有0,→0,上式右边就过渡为一个 积分。 X(w)eht 面积=jkw)ikw'a X(kwp)eikoct k+1)0 koo
因此, 就可以用 X(j ω )来表示 当 时,有 ,上式右边就过渡为一个 积分。 x( )t 0 0 0 0 0 1 1 () ( ) ( ) 2 jk t jk t k k x t X jk e X jk e T ω ω ω ω ω π +∞ +∞ =−∞ =−∞ = = T → ∞ 0 ω → 0

所以,一当0,→0,求和收敛于X(jo)ea的积分, 此时,T→∞,有()=x(),因此有: x(t)= x」“do 式4.8 X(jo)=x(t)ejdt 式4.9 式4.8和式4.9称为傅里叶变换对。函数Xiw)称为x() 的傅里叶变换或傅里叶积分,而式4.8称为傅里叶反 变换。 对照上一章讲的式3.38,都相当于把一个信号表示 为一组复指数信号的线性组合。对周期信号而言, 这些复指数信号的幅度为k,并且在成谐波关系的 一子 组离散点kw上出现。而对非周期信号而言,这 些复指数信号出现在连续频率上,其幅度为X(ω) (dw/2π)。X(w)通常称为x(t)的频谱
所以,当 ,求和收敛于 的积分, 此时, ,有 ,因此有: 式4.8和式4.9称为傅里叶变换对。函数X(j ω )称为 x ( t) 的傅里叶变换或傅里叶积分,而式4.8称为傅里叶反 变换 。 对照上一章讲的式3.38,都相当于把一个信号表示 为一组复指数信号的线性组合。对周期信号而言, 这些复指数信号的幅度为 a k,并且在成谐波关系的 一组离散点 k ω 0上出现。而对非周期信号而言,这 些复指数信号出现在连续频率上,其幅度为 X(j ω ) ( d ω/2 π)。 X(j ω )通常称为 x ( t)的频谱 。 ( ) j t X j e ω ω0 → 0 ω T → ∞ x() () t xt = 式4.8 式4.9 1 () ( ) 2 ( ) () j t j t x t Xj e d X j x t e dt ω ω ω ω π ω +∞ −∞ +∞ − −∞ = =

傅里叶变换 X(jo)=[x(t)e-idt w=2元X(juyedo 或者 x)←m→X(U0 傅里叶变换和傅里叶级数的关系: 4=xolew 周期信号)》 X(j0)=T·axlk,-o(非周期信号) 第4章连续时间傅里叶变换 20
第4章连续时间傅里叶变换 20 = = ∞+ ∞− +∞ ∞− − ωω π ω ω ω tx dejX dtetxjX tj tj )( 21 )( )()( 傅里叶变换和傅里叶级数的关系: 0 0 ( ) 1 ( )| () | k k k k a Xj ( ) T Xj Ta ω ω ω ω ω ω = = = = ⋅ 周期信号 非周期信号 或者 jXtx ω)()( ←⎯→FT 傅里叶变换