
3 Primer Plus,.(关)普拉塔(Prata,S.)著,云巅工作室译,人民郎电出版社,(第五版 4.The Art of Computer Programing,Donald E..Knuth(高德纳)译者:苏运霖,机械工业出版社 5.深入理解计算机系绕,Randal E.B肛yant/DavidR.0'allaron编若,机械工业出版社 七、本课程与其它课程的联系与分工 通过课程学习可以爹握编程的基本和方法,可较为轻松地学习其它程序设计语言,是后续的面向对 象程序设计基础I【、Jva架构编程等程序设计语言类课程的基础。 八、说明: 无 撰写人:冯国富 审核人:郑宗生 教学院长:袁红春 日期:2021年6月25日 2008 空间信息与数字技术系 Dept.Spatial informaion Digital technolog
3.Primer Plus,(美)普拉塔(Prata, S.) 著,云巅工作室译,人民邮电出版社 , (第五版) 4.The Art of Computer Programming,Donald E. Knuth(高德纳)译者:苏运霖,机械工业出版社 5.深入理解计算机系统,Randal E.Bryant / David R.O’Hallaron 编著 ,机械工业出版社 七、本课程与其它课程的联系与分工 通过课程学习可以掌握编程的基本和方法,可较为轻松地学习其它程序设计语言, 是后续的面向对 象程序设计基础 II、Java 架构编程等程序设计语言类课程的基础。 八、说明: 无 撰写人:冯国富 审核人:郑宗生 教学院长:袁红春 日期:2021 年 6 月 25 日

《线性代数》教学大纲 课程名称(中文/英文):《线性代数》(Linear A1 gebra)课程编号:1102129 学分:3学分 学时:总学时48学时 学时分配:讲授学时:48实验学时:0上机学时:0讨论学时:0其他学时:0 课程负责人:张蕾 1、课程衡介 1,课程概述 《线性代数》是高等院校的一门数学基础课。线性代数包括行列式、矩阵、线性相关性及方程组的求 解等内容,由于线性问题广泛存在于科学技术的各个领域,将非线性问题线性化十分重要。错助于计算机 来解大型线性方程组,求矩阵的特征值与特向量等已成为科学技术工作者经常遇到的课,因此学习和 掌握线性代数的理论和方法是掌握现代科学技术以及从事科学研究的重要基础和手段,本课程要求学生然 练掌握行列式的、矩阵的一些基本知识和方法,线性方程组及其有关的基本计算方法,并具有熟练的矩阵 运算能力和利用矩阵方法解决一些实际问题的能力。从而为后继课的学习及进一步提高览定必要的数学基 础。 Linear algebra is a basic course of aathematics in colleges sand universities.Linear r correlation and solution or equations. 21 and eige of matrices have and mastering the theory and methods of linear algebra is an important basis and means for astering modern science and technology and engaging in scientific research.This course requires students to master some basic knowledge and methods of determinants and matrices. linear equations and their related basic computational methods,and have the ability of matrix operation and solving some practical problems by atrix method.Thus,it lays the necessary ion for the subsequent courses and further improvement 2.课程目标 要程目标:通过学习线性代数的基本知识和基本理论,掌提信息领域复杂工程问题所需的数学知识,包括 常用的行列式、矩阵、向量和线性方程组基础知识。熟练进行行列式、矩阵的相关计算,能将相关代数知 识用于工程问题的表述。 课程目标2:掌提基于空思维建立和求解系统或过程数学模型所需的数学知识,能够运用线性方程组的 解的性质及解的结构、相似矩阵及正交对角化的概念用于工程问题的建模和求解。 课程目标3:能够利用内积、特征值和特征向量等知识对数字信息进行处理,分析结论的有效性,用于正确 表达空间信息获取、处理、分析和应用等方面的复杂工得问题。 课程目标4:利用二次型相关知识,能够正确处理数据,分析和解释结果,通过信息综合推断合理有效的研 究结论
《线性代数》教学大纲 课程名称(中文/英文):《线性代数》(Linear Algebra)课程编号:1102129 学分:3 学分 学时:总学时 48 学时 学时分配:讲授学时:48 实验学时:0 上机学时:0 讨论学时:0 其他学时:0 课程负责人:张蕾 1、 课程简介 1.课程概述 《线性代数》是高等院校的一门数学基础课。线性代数包括行列式、矩阵、线性相关性及方程组的求 解等内容。由于线性问题广泛存在于科学技术的各个领域,将非线性问题线性化十分重要。借助于计算机 来解大型线性方程组,求矩阵的特征值与特征向量等已成为科学技术工作者经常遇到的课题,因此学习和 掌握线性代数的理论和方法是掌握现代科学技术以及从事科学研究的重要基础和手段。本课程要求学生熟 练掌握行列式的、矩阵的一些基本知识和方法,线性方程组及其有关的基本计算方法,并具有熟练的矩阵 运算能力和利用矩阵方法解决一些实际问题的能力。从而为后继课的学习及进一步提高奠定必要的数学基 础。 Linear algebra is a basic course of mathematics in colleges and universities. Linear algebra includes determinant, matrix, linear correlation and solution of equations. Linear problems exist in many fields of science and technology, so it is very important to linearize them. Solving large-scale linear equations by computer and finding eigenvalues and eigenvectors of matrices have become a common problem for scientists and technicians. Therefore, learning and mastering the theory and methods of linear algebra is an important basis and means for mastering modern science and technology and engaging in scientific research. This course requires students to master some basic knowledge and methods of determinants and matrices, linear equations and their related basic computational methods, and have the ability of matrix operation and solving some practical problems by matrix method. Thus, it lays the necessary mathematical foundation for the subsequent courses and further improvement. 2. 课程目标 课程目标 1:通过学习线性代数的基本知识和基本理论,掌握信息领域复杂工程问题所需的数学知识,包括 常用的行列式、矩阵、向量和线性方程组基础知识,熟练进行行列式、矩阵的相关计算,能将相关代数知 识用于工程问题的表述。 课程目标 2:掌握基于空间思维建立和求解系统或过程数学模型所需的数学知识,能够运用线性方程组的 解的性质及解的结构、相似矩阵及正交对角化的概念用于工程问题的建模和求解。 课程目标 3:能够利用内积、特征值和特征向量等知识对数字信息进行处理,分析结论的有效性,用于正确 表达空间信息获取、处理、分析和应用等方面的复杂工程问题。 课程目标 4:利用二次型相关知识,能够正确处理数据,分析和解释结果,通过信息综合推断合理有效的研 究结论
课程目标与半业要求的关系炬阵 毕业要求指标点 1.1 1.2 2.2 4.4 课程目标1 课程目标2 课程目标3 课程目标4 附支撑点内容: 1.】(表述)掌提信息领域复杂工程问题所需的数学、自然科学、工程基础知识,并能将相关知识用 于工程问愿的表述,强化空间思锥与实验思维能力: 1.2(健模)掌握基于空间思维建立和求解系统或过程数学模型所需的致学、自然科学和工程基础知 识,并能将相关知识用于工程问题的建模和求解: 22(表达)具有系统观点,能基于相关科学原理和数学模型,正确表达空间信息获取、处理、分析和应用 等方面的复杂工程问题: 4.4(归纳)能够正确处理实验数据,分析和解释实验结果,通过信息综合得到合理有效的研究结论。 二、散学内容 1.论散学安排 教学内容 学时 备注 著列 8 作业为课后习题 行(列)展开 第二章矩阵 第四节短 初等变换与初等矩阵 10 作业为课后习题 的 第五节分块矩阵 我性方线为程组的基木概念 12 作业为课后习题
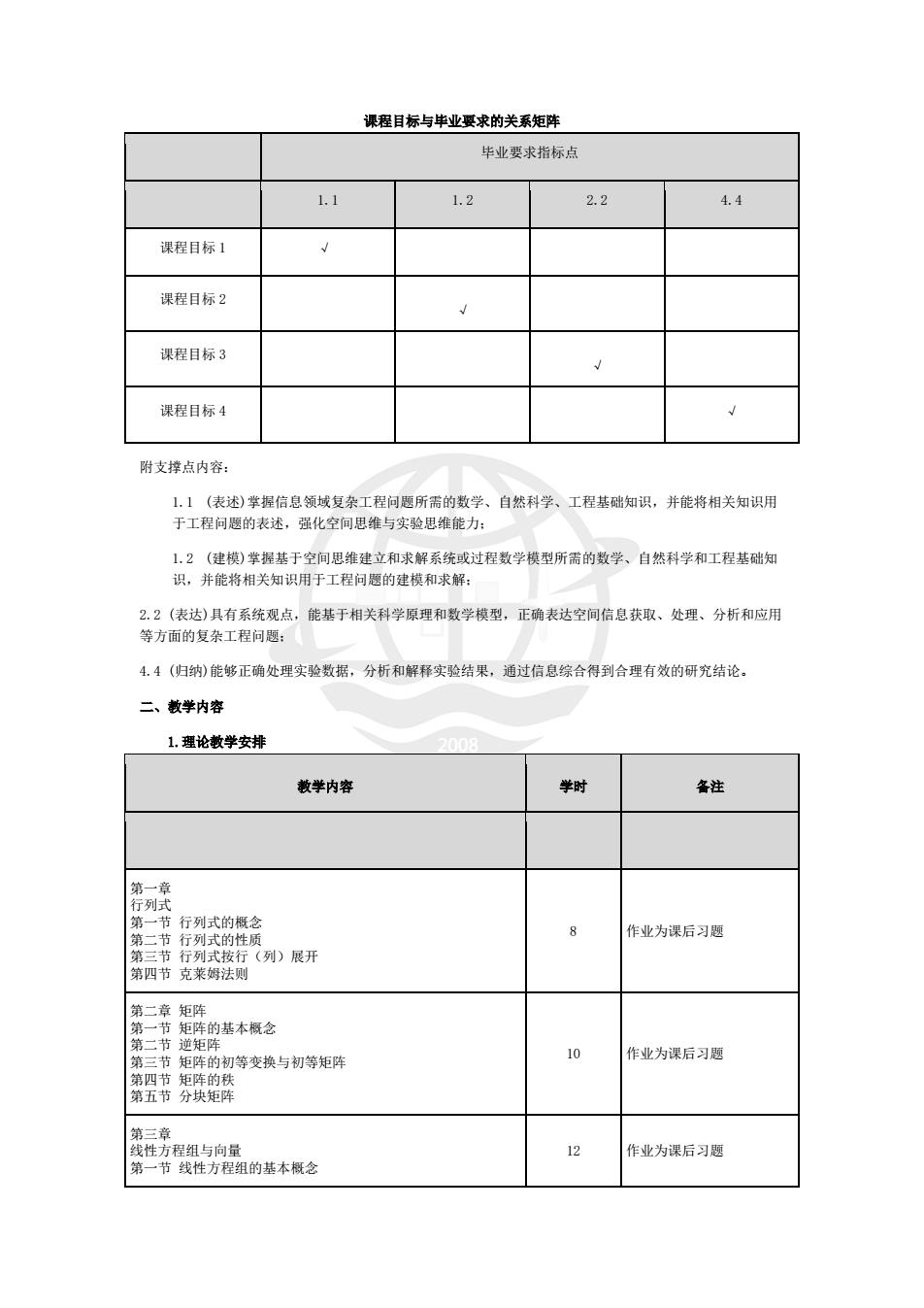
课程目标与毕业要求的关系矩阵 毕业要求指标点 1.1 1.2 2.2 4.4 课程目标 1 √ 课程目标 2 √ 课程目标 3 √ 课程目标 4 √ 附支撑点内容: 1.1 (表述)掌握信息领域复杂工程问题所需的数学、自然科学、工程基础知识,并能将相关知识用 于工程问题的表述,强化空间思维与实验思维能力; 1.2 (建模)掌握基于空间思维建立和求解系统或过程数学模型所需的数学、自然科学和工程基础知 识,并能将相关知识用于工程问题的建模和求解; 2.2 (表达)具有系统观点,能基于相关科学原理和数学模型,正确表达空间信息获取、处理、分析和应用 等方面的复杂工程问题; 4.4 (归纳)能够正确处理实验数据,分析和解释实验结果,通过信息综合得到合理有效的研究结论。 二、教学内容 1.理论教学安排 教学内容 学时 备注 第一章 行列式 第一节 行列式的概念 第二节 行列式的性质 第三节 行列式按行(列)展开 第四节 克莱姆法则 8 作业为课后习题 第二章 矩阵 第一节 矩阵的基本概念 第二节 逆矩阵 第三节 矩阵的初等变换与初等矩阵 第四节 矩阵的秩 第五节 分块矩阵 10 作业为课后习题 第三章 线性方程组与向量 第一节 线性方程组的基本概念 12 作业为课后习题
第节 10 作业为课后习圈 第五三次型 概念 作业为课后习避 三、教学方法 根据数学课程的特点。丰要采用多媒体课堂教学捕式。尝试微课、韩转课堂等多种教学辅式相结合, 注意详细讲解每节课的重点、难点内容,结合多媒体动画,加深学生对概念的理解。保证课上的练习时间, 可以及时针对问愿,当场解答。课下结合微信群、QQ群,及时解答学生在微题过程中的问题。 四、考核与评价方式及标准 1、考核与评价方式 成绩=期末成绩70%+平时成续30%。 (1)期末考试:闭卷,笔试。考试愿目应能客观反映出学生对课程内容的理解、掌提程度及综合运用 能力。 (2)平时成绩:每次课布置课下作业,配合2-3次课堂作业,加深学生对所学知识的理解和运用。 教学环节成绩比例(多) 成绩比例(男) 平时成绩 课程考试 课程目标1 8 19 之 课程目标2 8 21 高 课程目标3 8 18 课程目标4 6 2 18 合计(成绩构成》 100 2、考核与评价标准细
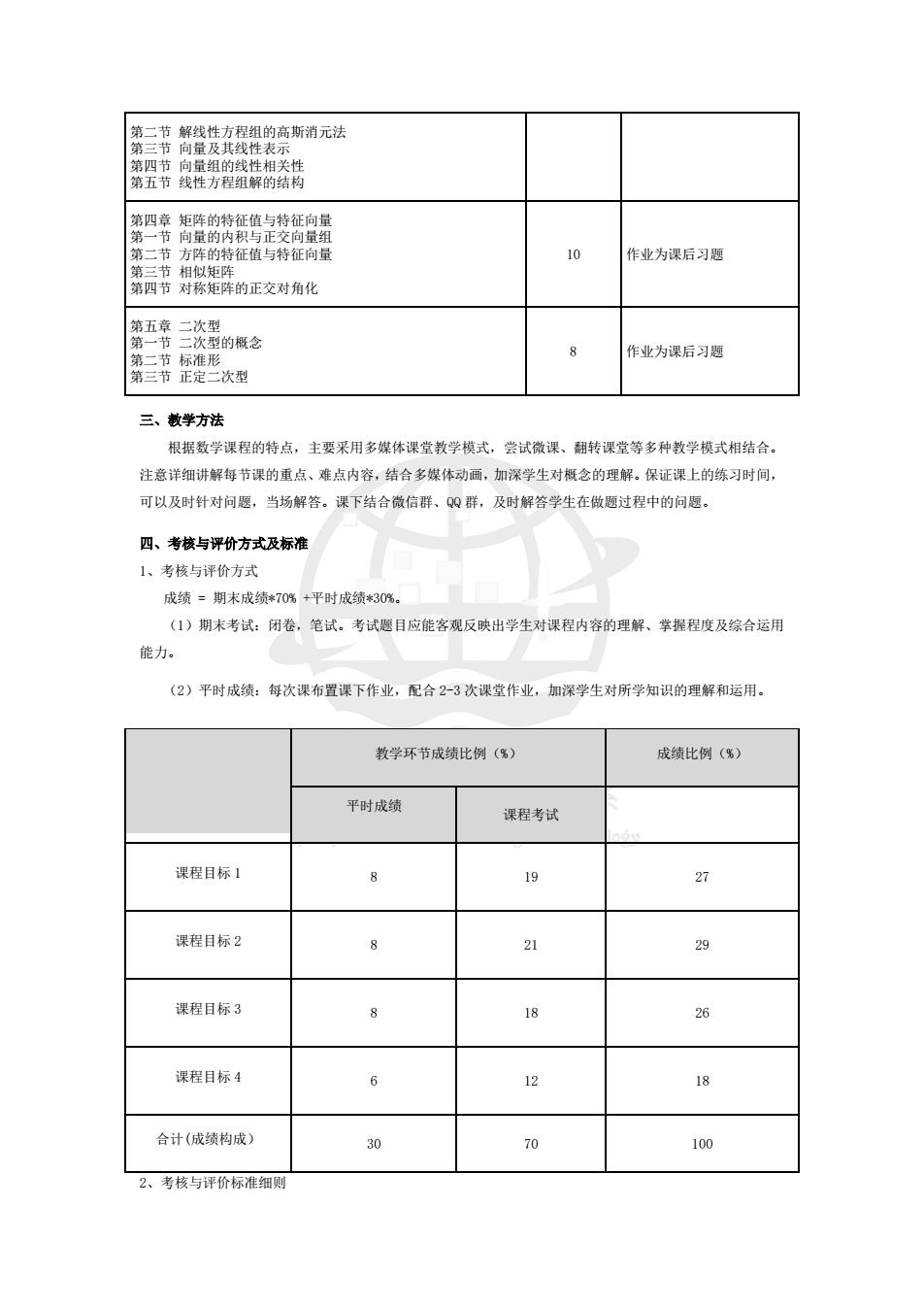
第二节 解线性方程组的高斯消元法 第三节 向量及其线性表示 第四节 向量组的线性相关性 第五节 线性方程组解的结构 第四章 矩阵的特征值与特征向量 第一节 向量的内积与正交向量组 第二节 方阵的特征值与特征向量 第三节 相似矩阵 第四节 对称矩阵的正交对角化 10 作业为课后习题 第五章 二次型 第一节 二次型的概念 第二节 标准形 第三节 正定二次型 8 作业为课后习题 三、教学方法 根据数学课程的特点,主要采用多媒体课堂教学模式,尝试微课、翻转课堂等多种教学模式相结合。 注意详细讲解每节课的重点、难点内容,结合多媒体动画,加深学生对概念的理解。保证课上的练习时间, 可以及时针对问题,当场解答。课下结合微信群、QQ 群,及时解答学生在做题过程中的问题。 四、考核与评价方式及标准 1、考核与评价方式 成绩 = 期末成绩*70% +平时成绩*30%。 (1)期末考试:闭卷,笔试。考试题目应能客观反映出学生对课程内容的理解、掌握程度及综合运用 能力。 (2)平时成绩:每次课布置课下作业,配合 2-3 次课堂作业,加深学生对所学知识的理解和运用。 教学环节成绩比例(%) 成绩比例(%) 平时成绩 课程考试 课程目标 1 8 19 27 课程目标 2 8 21 29 课程目标 3 8 18 26 课程目标 4 6 12 18 合计(成绩构成) 30 70 100 2、考核与评价标准细则
(1)期末考试成绩:70%。考试范围几乎通盖所有讲授的内容,主要题型为:判新愿、选择愿、填空 题、计算题和证明题 评价标准 基本要求 优秀(90-100) 良好(70-89】 合格(60-69) 不合格(60) 基本概念表述正确, 基本据今表述基本基本概今不清 论 思 课程目标1 及格 掌提线性方程组的 较好草提线性方格 基本草线性方程 能李提线性方程到 度的 课程涉及的工程。 课程涉及的工程问涉及的工程问 课程目标2 绩及格 期末 其太成抽 成 课程目标3 结 星问思,成锁良好 工程品题 成结及绩不及格。 能够正确处理实 能够较好地正确处 基本能够正确处理 不能正确处理实验翌 数据,分析和解释实 课程目标4 合得到合理有效的 信息综合得到合理 良所究结论。 得到合理有效的研究 成绩及格究 结论,成绩不及格。 」 (2)平时成敛 评价标准 基本要求 优秀 良好 的 不合格 误堂表现活跃,按时 课堂表现良好,按时 域复杂工程趣 信领域城复杂工 本掌信息领域匀 现象,不能掌信 需的数 所需的 平时 成绩课程目标1 并能将相关 知识月 只,并能将相关为 础知识 工程基知 化空间思维与 具有空间思维上 不 ,阶月 练习成良好 阶段练习成绩不及格。 绩及格
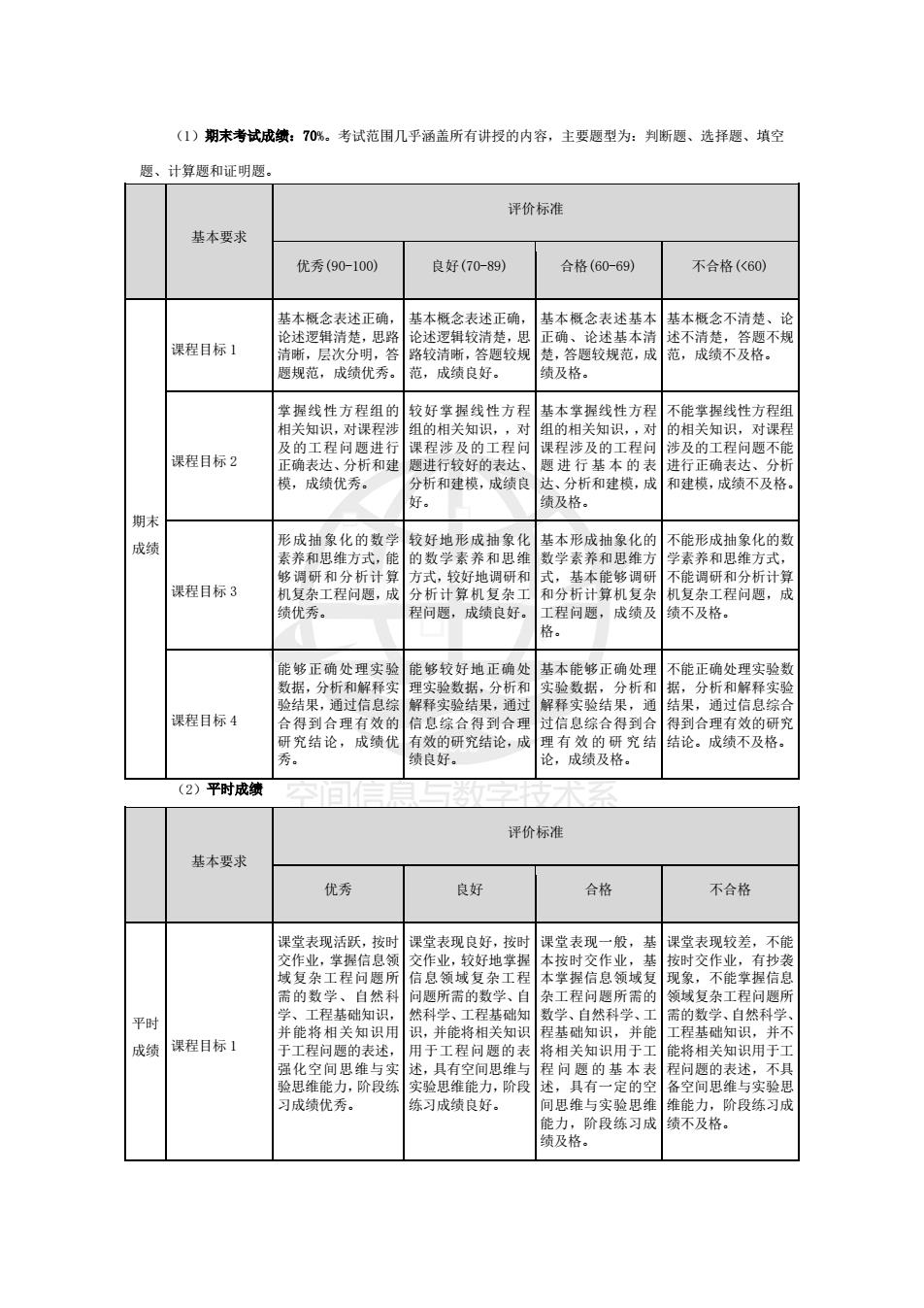
(1)期末考试成绩:70%。考试范围几乎涵盖所有讲授的内容,主要题型为:判断题、选择题、填空 题、计算题和证明题。 基本要求 评价标准 优秀(90-100) 良好(70-89) 合格(60-69) 不合格(<60) 期末 成绩 课程目标 1 基本概念表述正确, 论述逻辑清楚,思路 清晰,层次分明,答 题规范,成绩优秀。 基本概念表述正确, 论述逻辑较清楚,思 路较清晰,答题较规 范,成绩良好。 基本概念表述基本 正确、论述基本清 楚,答题较规范,成 绩及格。 基本概念不清楚、论 述不清楚,答题不规 范,成绩不及格。 课程目标 2 掌握线性方程组的 相关知识,对课程涉 及的工程问题进行 正确表达、分析和建 模,成绩优秀。 较好掌握线性方程 组的相关知识,,对 课程涉及的工程问 题进行较好的表达、 分析和建模,成绩良 好。 基本掌握线性方程 组的相关知识,,对 课程涉及的工程问 题 进 行 基 本 的 表 达、分析和建模,成 绩及格。 不能掌握线性方程组 的相关知识,对课程 涉及的工程问题不能 进行正确表达、分析 和建模,成绩不及格。 课程目标 3 形成抽象化的数学 素养和思维方式,能 够调研和分析计算 机复杂工程问题,成 绩优秀。 较好地形成抽象化 的数学素养和思维 方式,较好地调研和 分析计算机复杂工 程问题,成绩良好。 基本形成抽象化的 数学素养和思维方 式,基本能够调研 和分析计算机复杂 工程问题,成绩及 格。 不能形成抽象化的数 学素养和思维方式, 不能调研和分析计算 机复杂工程问题,成 绩不及格。 课程目标 4 能够正确处理实验 数据,分析和解释实 验结果,通过信息综 合得到合理有效的 研究结论,成绩优 秀。 能够较好地正确处 理实验数据,分析和 解释实验结果,通过 信息综合得到合理 有效的研究结论,成 绩良好。 基本能够正确处理 实验数据,分析和 解释实验结果,通 过信息综合得到合 理 有 效 的 研 究 结 论,成绩及格。 不能正确处理实验数 据,分析和解释实验 结果,通过信息综合 得到合理有效的研究 结论。成绩不及格。 (2)平时成绩 基本要求 评价标准 优秀 良好 合格 不合格 平时 成绩 课程目标 1 课堂表现活跃,按时 交作业,掌握信息领 域复杂工程问题所 需的数学、自然科 学、工程基础知识, 并能将相关知识用 于工程问题的表述, 强化空间思维与实 验思维能力,阶段练 习成绩优秀。 课堂表现良好,按时 交作业,较好地掌握 信息领域复杂工程 问题所需的数学、自 然科学、工程基础知 识,并能将相关知识 用于工程问题的表 述,具有空间思维与 实验思维能力,阶段 练习成绩良好。 课堂表现一般,基 本按时交作业,基 本掌握信息领域复 杂工程问题所需的 数学、自然科学、工 程基础知识,并能 将相关知识用于工 程 问 题 的 基 本 表 述,具有一定的空 间思维与实验思维 能力,阶段练习成 绩及格。 课堂表现较差,不能 按时交作业,有抄袭 现象,不能掌握信息 领域复杂工程问题所 需的数学、自然科学、 工程基础知识,并不 能将相关知识用于工 程问题的表述,不具 备空间思维与实验思 维能力,阶段练习成 绩不及格