
」.5逻辑函数及其表示方法 .17 1.5逻辑函数及其表示方法 1.5.1逻辑函数 从上面讲过的各种逻辑关系中可以看到,如果以逻辑变量作为输入,以运算 结果作为输出,那么当翰人变量的取值确定之后,输出的取值便随之而定。因 此,输出与输人之间乃是一种函数关系。这种函数关系称为逻辑函数,写作 Y=F(A,B,C,.) 由于变量和输出(函数)的取值只有0和1两种状态,所以我们所讨论的都是二 值逻辑函数 任何一件具体的因果关系都可以用一个逻辑函数描述。例如,图1.5.1是 一个举重栽判电路,可以用一个逻辑函数描述它的逻辑功能 比赛规则规定,在一名主裁判和两名副 裁判中,必须有两人以上(而且必须包括主裁 判)认定运动员的动作合格,试举才算成功。 此赛时主裁判掌握若开关A,两名副裁判分 别举握着开关B和C。当运动员举起杠铃 时,裁判认为动作合格了就合上开关,否则不 合。显然,指示灯Y的状态(亮与暗)是开关 图1.5,1举重裁判电路 A,B、C状态(合上与晰开)的函数。 若以1表示开关闭合,0表示开关断开:以1表示灯亮,以0表示灯暗,则指 示灯Y是开关A,B、C的二值逻辑函数,即 Y=F(A,B,C) 1.5.2逻辑函数的表示方法 常用的逻辑函数表示方法有逻辑真值表(简称真值表)、逻辑函数式(也称逻 辑式或函数式)、逻辑图和卡诺图等。这一节只介绍前面三种方法,用卡诺图表 示逻辑函数的方法将在后面作专门介绍。 一、更辑真值表 将输人变量所有的取值下对应的输出值找出来,列成表格,即可得到真值 表

·18 第一章逻辑代敛基碰 仍以图1.5.1的举重裁判电路为例,根据电路的工作原理不难看出,只有 A=1,同时B、C至少有个为1时Y才等于1,于是可列出图1.5.1的真值 表。 二、逻辑函数式 把输出与输入之间的逻辑关系写成与、或、非等运算的组合式,即逻辑代数 式,就得到了所需的逻辑函数式。 表15.1图1.5.1电路的真值表 输出 A Y 0 0 0 0 0 1 0 0 1 0 1 1 0 0 0 0 1 1 0 1 1 1 11 在图1.5.1电路中,根据对电路功能的要求和与、或的逻辑定义,“B和C 中至少有一个合上”可以表示为(B+C),“同时还要求合上A”,则应写作 A·(B+C),因此得到输出的逻辑函数式为 Y=A(B+C) (1.5.1) 三、逻辑图 将逻辑函数中各变量之间的与、或、非等逻辑关系用图形符号表示出来,就 可以画出表示函数关系的逻辑图。 为了出表示图1.5.1电路功能的逻辑图,只要用逻辑运算的图形符号代 替式(1.5.1)中的代数运算符号便可得到图1.5.2所示的逻辑图。 四、各种表示方法间的互相转换 既然同一个逻辑函数可以用三种不同的方A一 法描述,那么这三种方法之间必能互相转换。 经常用到的转换方式有以下几种。 C 1.从真值表写出逻辑函数式 图1.52图1.5.1电路的辑图 为便于理解转换的原理,先讨论一个具体

1.5漫辑函数及其表示方法 ·19- 的例子。 【例1.5,1】已知一个奇偶判别函数的真值表如表1.5.2所示,试写出它 的逻辑函数式。 表1.5,2例1.5.1的函数真值表 A c Y 0 0 0 0 0 0 1 0 0 1 0 1 .ABc 0 -ABC 1 1 0 解:由真值表可见,只有当A、B、C三个输入变量中两个同时为1时,Y 才为1。因此,在输入变量取值为以下三种情况时,Y将等于1: A=0、B=1,C=1 A=1、B=0、C=1 A=1、B=1、C=0 而当A=0、B=1、C=1时,必然使乘积项ABC=1;当A=1、B=0,C=1时,必 然使乘积项ABC=1;当A=1,B=1、C=0时,必然使ABC=1,因此Y的逻辑 函数应当等于这三个乘积项之利,即 Y=ABC+ABC+ABC 通过(例1.5.1】可以总结出从真值表写出逻辑函数式的一般方法,这就是 ①找出真值表中使逻辑函数Y=1的那些输入变量取值的组合: ②每组输入变量取值的组合对应一个乘积项,其中取值为1的写人原变 量,取值为0的写入反变量。 ③将这些乘积项相加,即得Y的逻朝函数式。 2.从逻辑式列出真值表 将输入变量取值的所有组合状态逐一代入逻辑式求出函数值,列成表,即可 得到真值表。 【例1.5,2】已知逻辑函数Y=A+BC+ABC,求它对应的真值表。 解:将A、B、C的各种取值逐一代入Y式中计算,将计算结果列表,即得 表1.5.3的真值表。初学时为避免差错可先将BC、ABC两项算出,然后将A、 BC和ABC相加求出Y的值
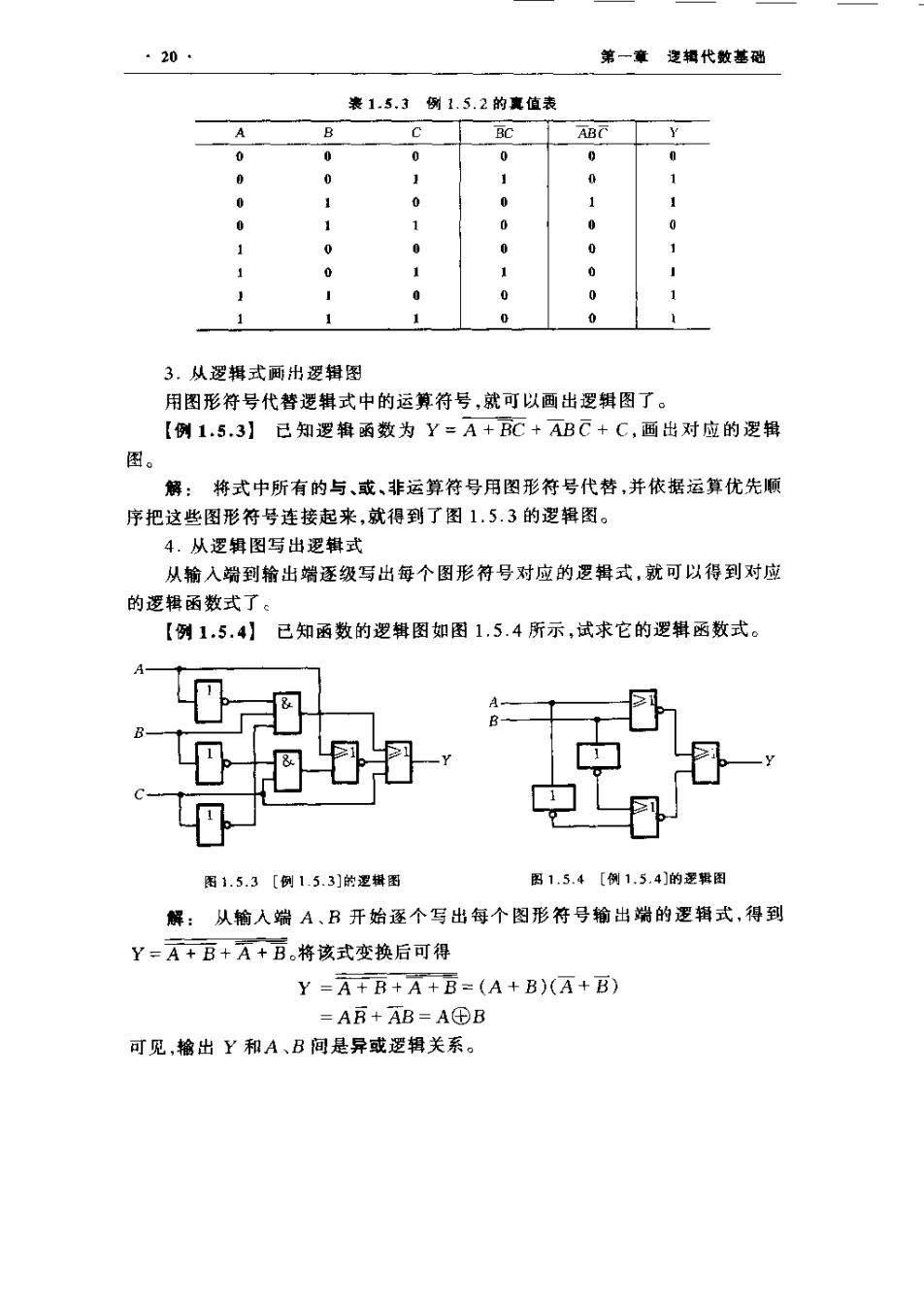
·20· 第一章逻辑代数基础 表1.5.3例1.5.2的夏值表 ABC 0 1 0 0 3.从逻辑式画出逻辑图 用图形符号代誓逻辑式中的运算符号,就可以画出逻辑图了。 【例1.5.3】已知逻辑函数为Y=A+C+ABC+C,画出对应的逻辑 解:将式中所有的与、或、非运算符号用图形符号代替,并依据运算优先顺 序把这些图形符号连接起来,就得到了图1.5.3的逻辑图。 4.从逻辑图写出逻辑式 从输入端到输出端逐级写出每个图形符号对应的逻辑式,就可以得到对应 的逻辐函数式了: 【例1.5.4】已知函数的逻辑图如图1.5.4所示,试求它的逻辑函数式。 图1.5.3〔例1.5.3)的逻辑图 图1.5.4[例1.5.4的是图 解:从输入端A、B开始逐个写出每个图形符号输出端的逻辑式,得到 Y=A+B+A+B。将该式变换后可得 Y=A+B+A+B=(A+B)(A+B) =AB+AB=A⊕B 可见,输出Y和A、B间是异或逻相关系
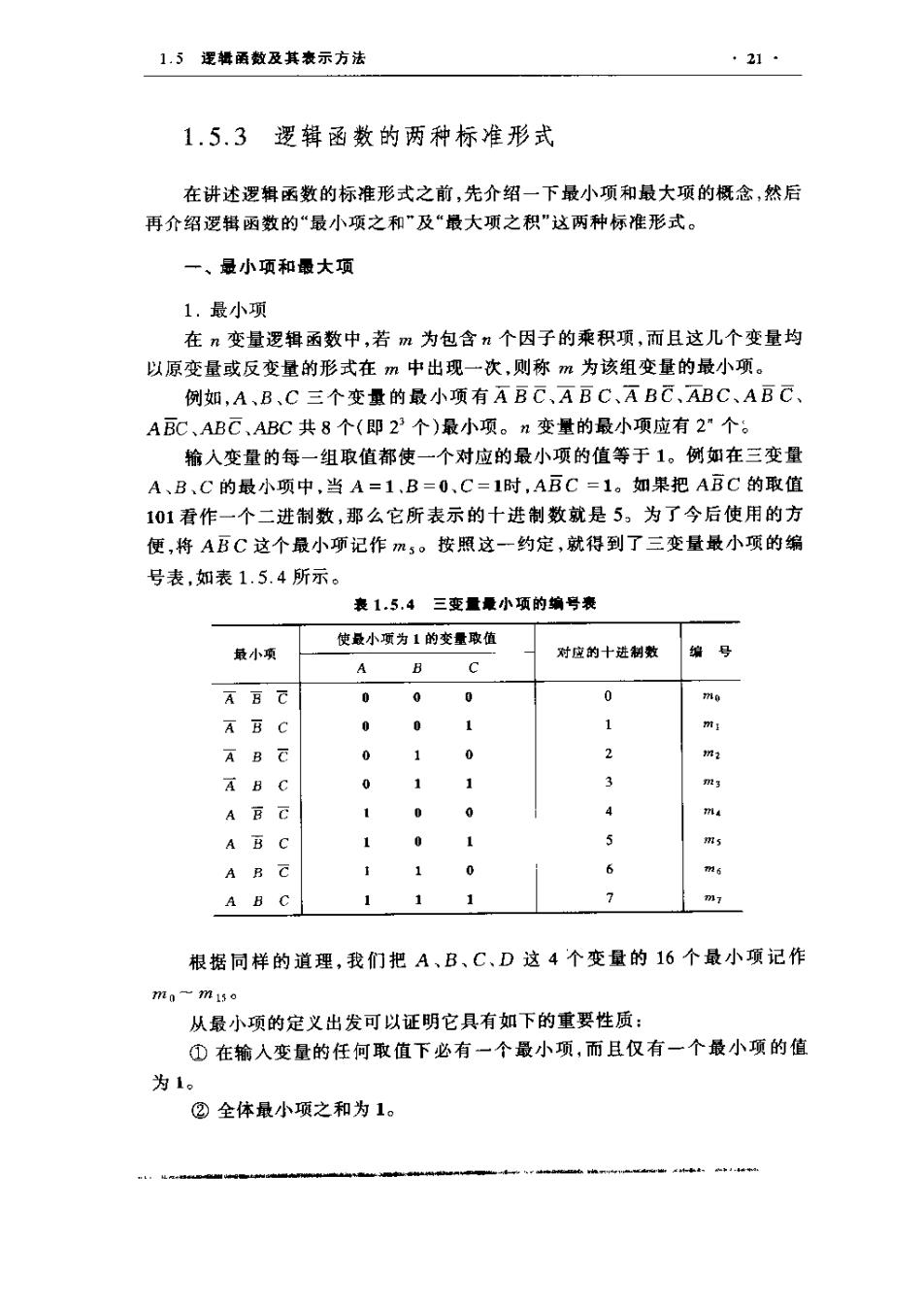
1.5逻辑函数及其表示方法 ·21· 1.5.3逻辑函数的两种标准形式 在讲述逻辑函数的标准形式之前,先介绍一下最小项和最大项的概念,然后 再介绍逻辑函数的“最小项之和“及“最大项之积”这两种标准形式。 一、最小项和最大项 1.最小项 在n变量逻辑函数中,若m为包含”个因子的乘积项,而且这儿个变量均 以原变量或反变量的形式在m中出现一次,则称m为该组变量的最小项。 例如,A、B、C三个变量的最小项有ABC,ABC、ABC、ABC、ABC ABC、ABC、ABC共8个(即2个)最小项。n变量的最小项应有2”个 输入变量的每一组取值都使一个对应的最小项的值等于1。例如在三变量 A、B、C的最小项中,当A=1,B=0、C=1时,ABC=1。如果把A豆C的取值 101看作一个二进制数,那么它所表示的十进制数就是5,为了今后使用的方 便,将ABC这个最小项记作m5。按照这-一约定,就得到了三变量最小项的编 号表,如表1.5.4所示。 表1.5.4三变量小项的编号表 使最小项为1的变量政植 最小项 对应的十进制数 编号 A C A B C 0 0 0 0 不BC 1 A B C 0 1 0 A B C 1 3 A万C 0 4 A B C 1 1 5 A R C ABC 1 1 1 1 根据同样的道理,我们把A、B、C、D这4个变量的16个最小项记作 ma-miso 从最小项的定义出发可以证明它具有如下的重要性质: ①在输入变量的任何取值下必有一个最小项,而且仅有一个最小项的值 为1。 ②全体最小项之和为1