
(2)欧拉法的特点具体如下: 1)欧拉法实际上是采用折线代替了实际曲线,也称之为折线法。 2)此类方法计算简单,容易实现。由前一点值y仅一步递推就可以求出后一点值yk+1, 称为单步法。 3)欧拉法处理时,只要给定初始值y。,即可开始进行递推运算,不需要其他信息,因此 它属于自启动模式。 4)由于欧拉法是一种近似的处理,存在计算误差,所以系统的计算精度较低。若要提高 计算精度,只能减小计算步长,但由于计算机字长有限,再加上增加了计算工作量,使用仿真 速度受到限制。 5)通常,欧拉法仿真方法简单,计算量小,多适用于精度要求不高的场合
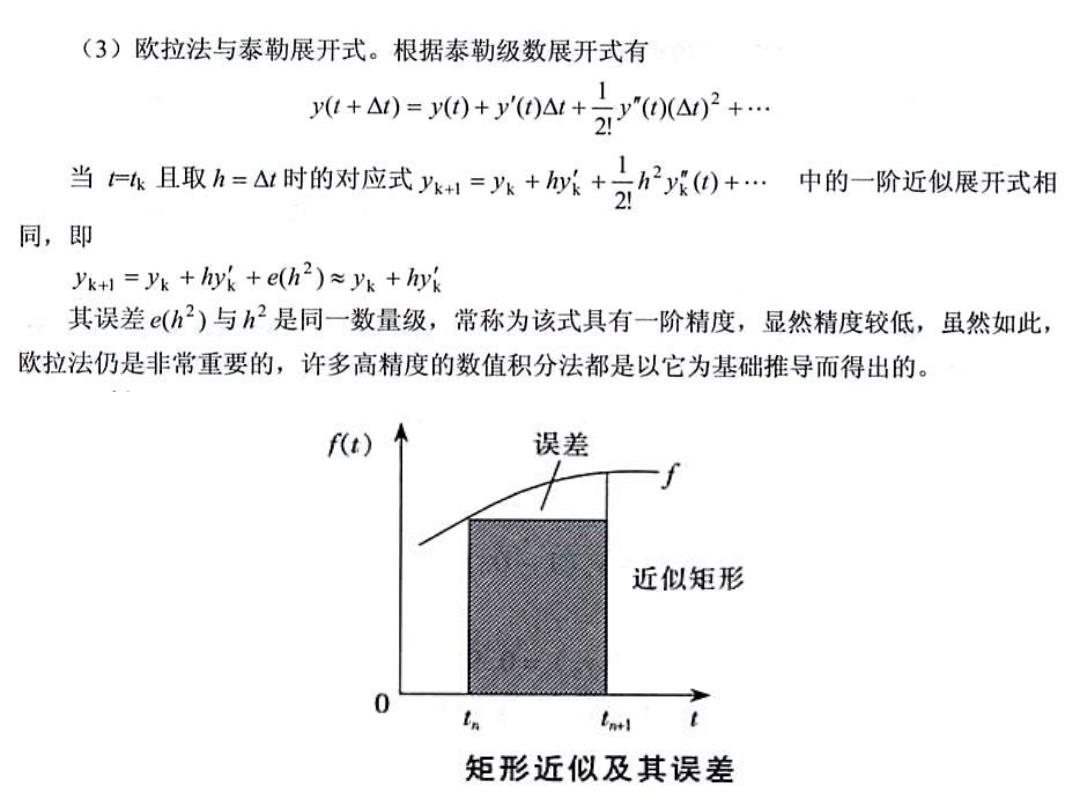
(3)欧拉法与泰勒展开式。根据泰勒级数展开式有 t+a)=0+0aw+yr0a2+ 当且取h=加时的对应式=%+城+分0+… 中的一阶近似展开式相 同,即 yk+=yk +hyk +e(h2)yk +hyk 其误差(h2)与h2是同一数量级,常称为该式具有一阶精度,显然精度较低,虽然如此, 欧拉法仍是非常重要的,许多高精度的数值积分法都是以它为基础推导而得出的。 f(t) 误差 近似矩形 0 Enel 矩形近似及其误差

例 设系统方程为: y+y2=0,y(0)=1 试用欧拉法求其数值解(取步长h=0.1,0≤t≤1)。 解:原方程为夕=-y,f八t,y)=-y 递推公式为: ym+1=yn+hf(tn,yn)=yn(1-0.1yn) o=0,y0=1 t1=0.1,y1=ya(1-0.1yo)=0.9 t2=0.2,y2=y1(1-0.1y1)=0.819 t10=1.0,y10=yg(1-0.1yg)=0.4628 已知方程的解析解为y=十。精确解与解析解比较如下:
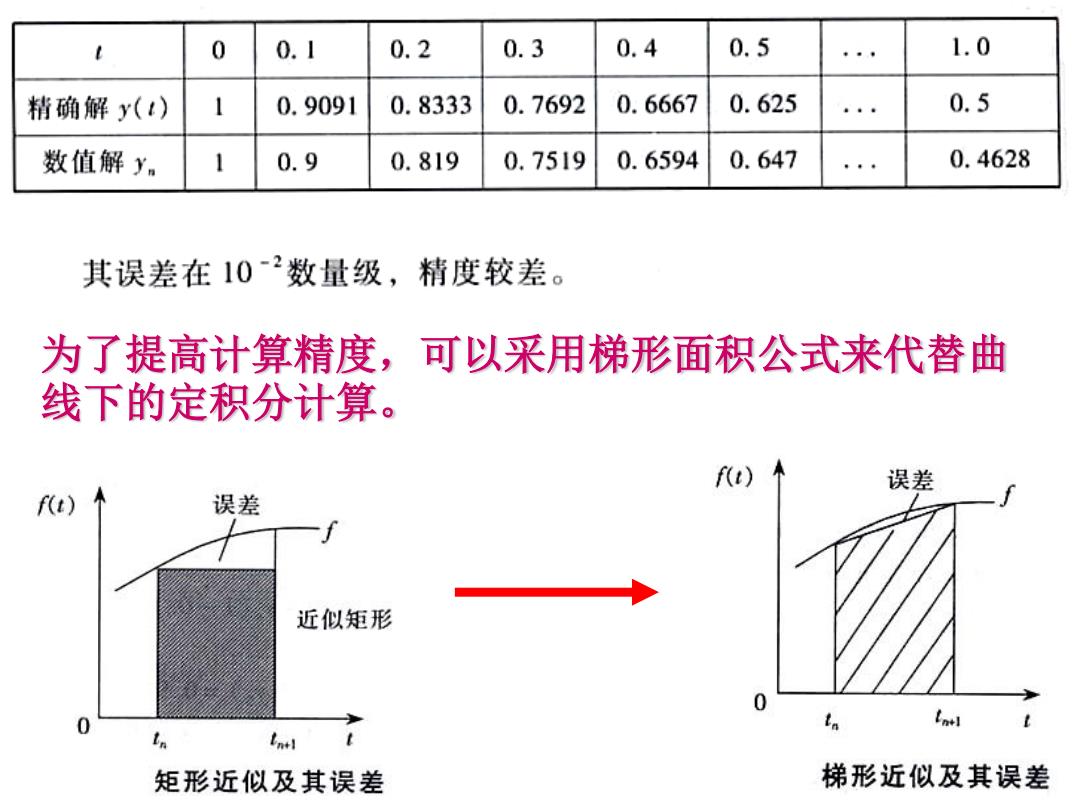
0 0.1 0.2 0.3 0.4 0.5 1.0 精确解y() 1 0.9091 0.8333 0.7692 0.6667 0.625 0.5 数值解y 0.9 0.819 0.7519 0.6594 0.647 0.4628 其误差在102数量级,精度较差。 为了提高计算精度,可以采用梯形面积公式来代替曲 线下的定积分计算。 ft) 误差 f(t) 误差 近似矩形 0 0 In Inel 矩形近似及其误差 梯形近似及其误差
为了提高计算精度,可以采用梯形面积公式来代替曲 线下的定积分计算
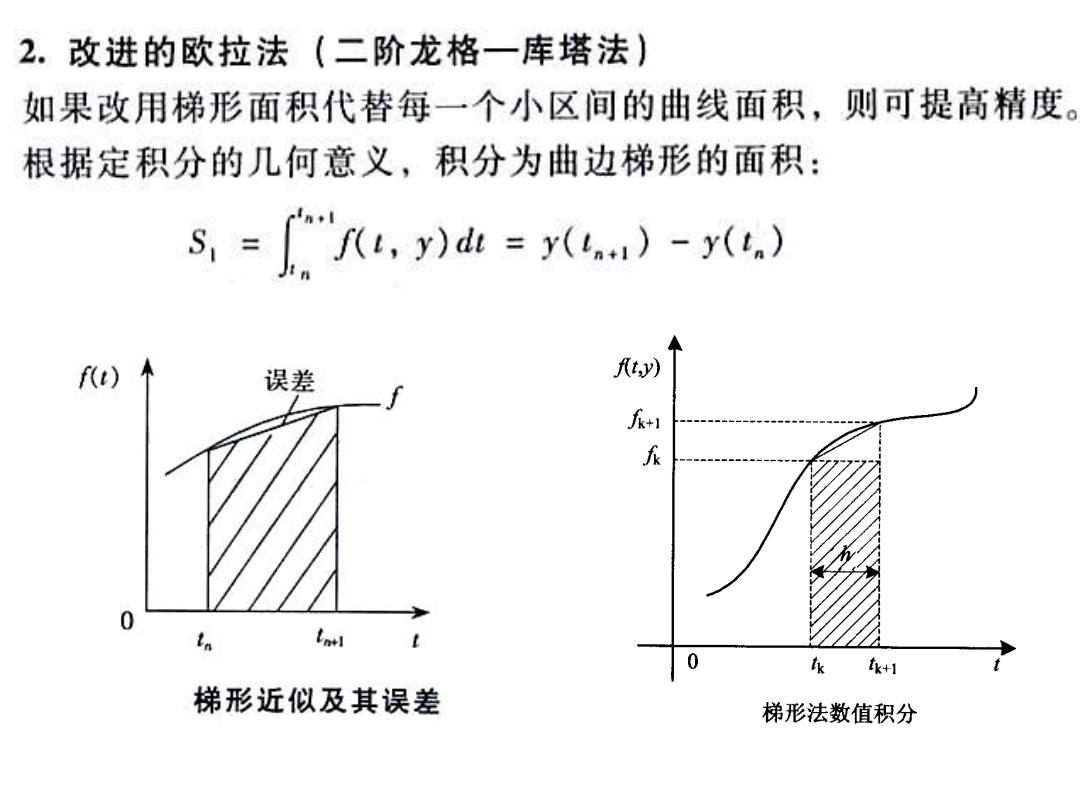
2.改进的欧拉法(二阶龙格一库塔法) 如果改用梯形面积代替每一个小区间的曲线面积,则可提高精度 根据定积分的几何意义,积分为曲边梯形的面积: 5,=,y)=y()-y(.) f(t) 误差 +1 众 0 Entl 0 k fk+1 梯形近似及其误差 梯形法数值积分