
一、常用的几种数值积分法 ■数值积分法可分为两大类: 单步法、多步法。 ■如果由当前时刻的数值yn, 就能求出后一时刻的 数值y+1,此外不需要其他时刻的任何信息,称 这种方法为单步法。 ■反之,为了求得tn+1,时刻的近似值yn+1? 不仅需 要知道t时刻的近似值yn,而且还要用到过去时 刻tn-1,tn-2,处的数据,则称这种方法为多步 法
一、常用的几种数值积分法 数值积分法可分为两大类:单步法、多步法。 如果由当前时刻的数值yn,就能求出后一时刻的 数值yn+1,此外不需要其他时刻的任何信息,称 这种方法为单步法。 反之,为了求得tn+1,时刻的近似值yn+1,不仅需 要知道tn时刻的近似值yn,而且还要用到过去时 刻tn-1,tn-2,…处的数据,则称这种方法为多步 法

(一) 单步法 1、欧拉(Euer)法(一阶龙格-库塔法) ■()欧拉公式的推导 ■设某系统的常微分方程为 =ft,》 dt y(to)=yo 式中: f(t,y):包含有时间和函数y的表达式: yo:函数y在初始时刻t时的对应初值
(一) 单步法 1、欧拉(Euler)法(一阶龙格-库塔法) (1)欧拉公式的推导 设某系统的常微分方程为 y t y f t y dt dy 0 0 ( ) ( , ) 式中: f(t,y):包含有时间t和函数y的表达式; y0:函数y在初始时刻t0时的对应初值

d砂=ft,y) dt t)=y。 将上式在小区间[k,k]上进行积分可得 1-4=fd.() 又由导数定义知 d业=lim (t+△)-y() dt-→0 △t 在t=k时刻,取计算步长h=△1=k+1-k,显然有:yk1=y(+△),yk=y()。设h足 够小,使得 出=)”.@
y t y f t y dt dy 0 0 ( ) ( , )
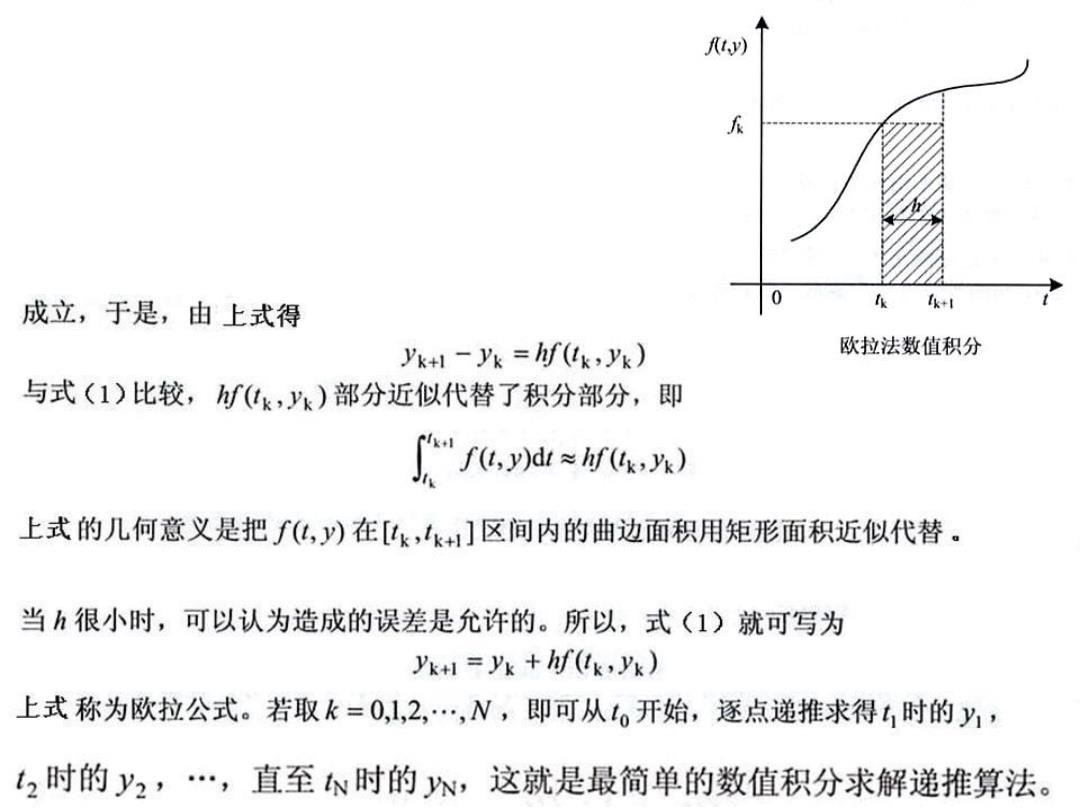
成立,于是,由上式得 k lk+l yk+-yk =hf(tk,yg) 欧拉法数值积分 与式(1)比较,(k,yk)部分近似代替了积分部分,即 f心,出≈e, 上式的几何意义是把f化,y)在[k,k1]区间内的曲边面积用矩形面积近似代替。 当h很小时,可以认为造成的误差是允许的。所以,式(1)就可写为 yk+=yx +hf(ik,yx) 上式称为欧拉公式。若取k=01,2,…,N,即可从o开始,逐点递推求得4时的y1, t2时的y2,…,直至N时的,这就是最简单的数值积分求解递推算法
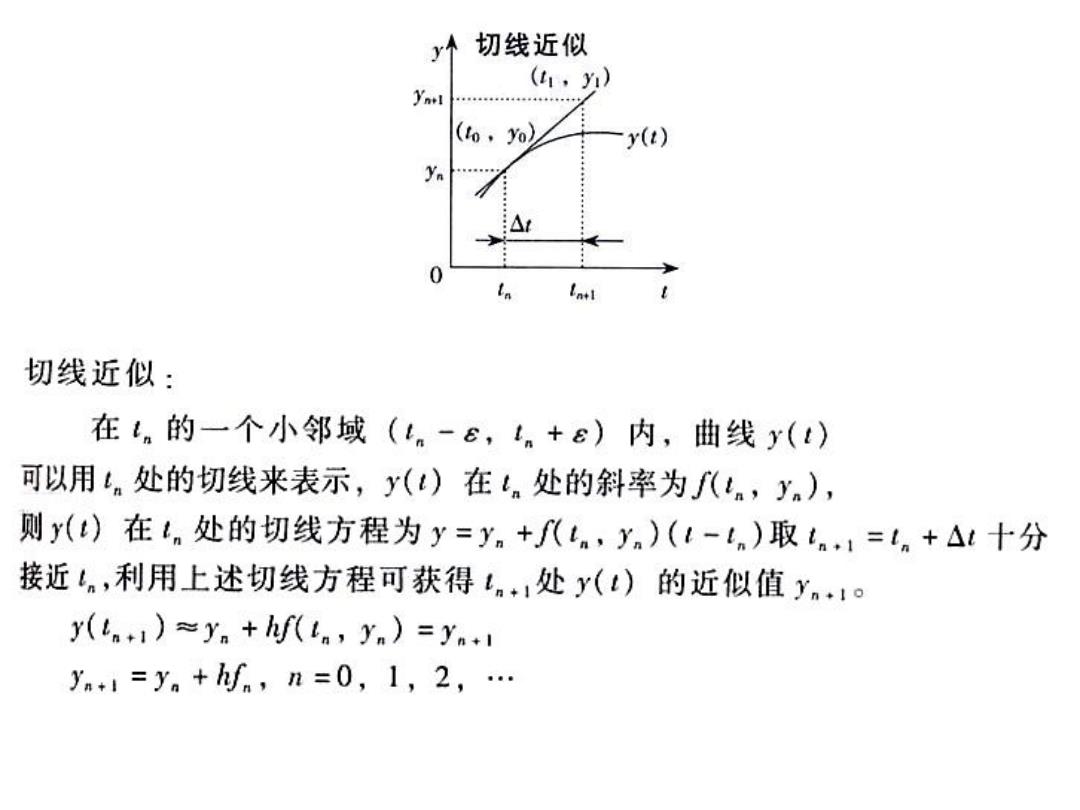
切线近似 (1,) (to,yo) y(t) yn 切线近似: 在t。的一个小邻域(t。-e,tn+ε)内,曲线y(t) 可以用tn处的切线来表示,y(t)在tn处的斜率为f(t。,yn), 则y(t)在tn处的切线方程为y=yn+f八n,yn)(l-tn)取tn1=tn+At十分 接近。,利用上述切线方程可获得1n1处y(t)的近似值y.1 y(n+1)≈yn+hf(a,yn)=yn+i y+=y+hf,n=0,1,2