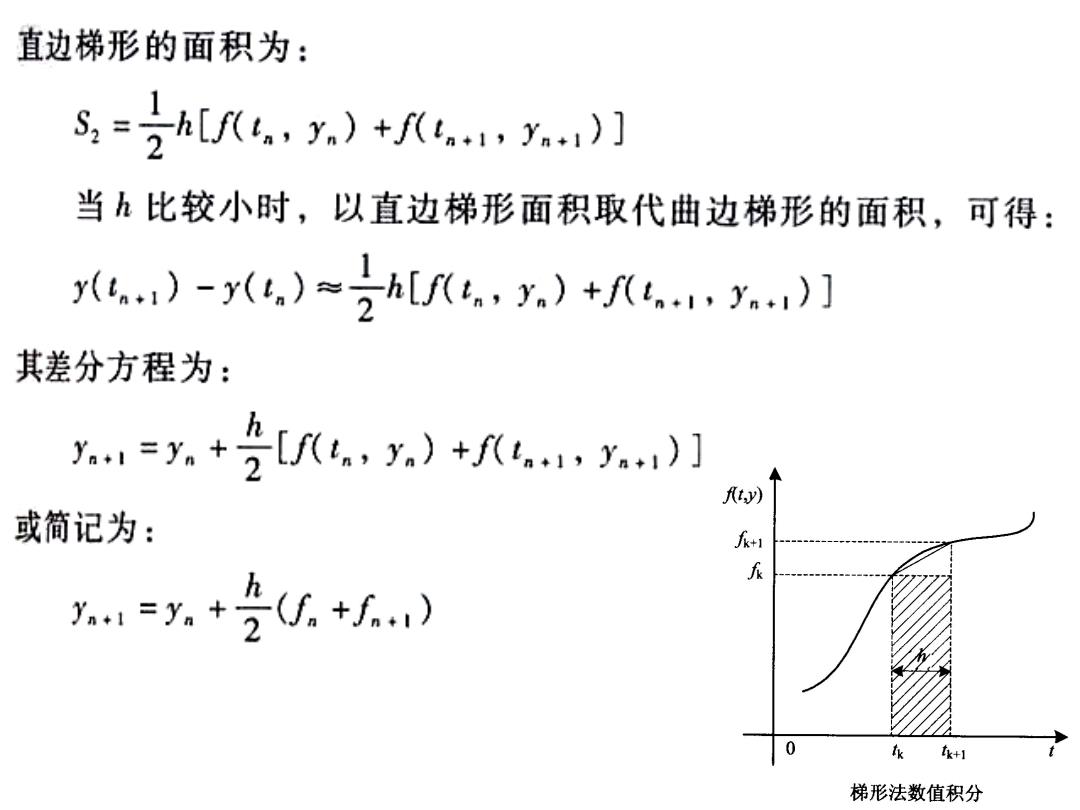
直边梯形的面积为: S,=2h[x)+4,】 当h比较小时,以直边梯形面积取代曲边梯形的面积,可得: y)-y(.)=2)+…)] 其差分方程为: y=.+[/,y.)+1,yi)] fty) 或简记为: 1=+.+以) +灯 梯形法数值积分

上式是一隐函数形式,公式右端含有待求量y.1, 故不能自行起步运算,而需有其他算法的帮助。 比如,每次计算都用欧拉法求出初值,算出y()的近似值y1, 然后将其代入原微分方程右端,计算导函数∫ 的近似值,=f(n+1,y,),最后利用梯形公式求出修正后的y1。为 了提高计算精度通常需要迭代运算,即先用欧拉法估计一个初值y,然 后用下式求出y”。 =y.+[,)+…)】 再用y,去求y
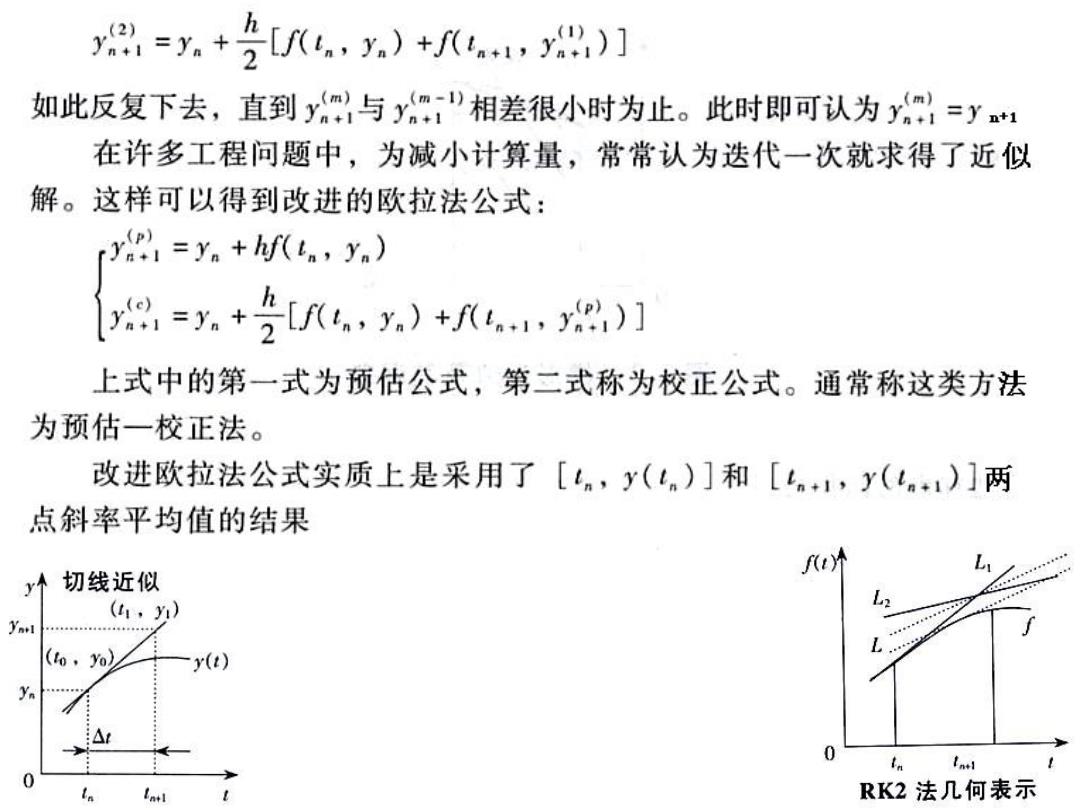
y=.+[)+u门 如此反复下去,直到y与y:”相差很小时为止。此时即可认为y=y 在许多工程问题中,为减小计算量,常常认为迭代一次就求得了近似 解。这样可以得到改进的欧拉法公式: =yhf(ty) 8,=+[6,.)+1,)】 上式中的第一式为预估公式,第二式称为校正公式。通常称这类方法 为预估一校正法。 改进欧拉法公式实质上是采用了[n,y()]和[.+1,y(n1)]两 点斜率平均值的结果 f 切线近似 (4,y) Yael (,yo) y() yn 0 Indl RK2法几何表示

y1=y。+2h(k,+k) k=f=f(t,y) k2=f=f(,y)=f(ta,y+hk) 由于它利用了两个点的信息,从而提高了计算精度。这一思想被广泛 地应用于许多算法之中。在实际计算中并非一定要取斜率平均值,而可以 采用加权平均,如果在每个积分步中多取几个点,分别求出其斜率k, k2,…k,然后取不同的权值,则公式为: k=0k+0,k+…+,k,=∑0,k:

梯形公式: n1=%+e,)+few】 梯形积分公式,也称为亚当姆斯(Adams)公式。 从梯形积分公式中可以看到,在计算yk+时,其右端函数中 也含有yk+1,这种公式称为隐式公式,不能靠自身解决,需 要采用迭代方法来启动,称之为多步法。 其基本处理方法就是采用欧拉公式进行预报,采用梯形公式 进行校正,即
梯形公式: 梯形积分公式,也称为亚当姆斯(Adams)公式。 从梯形积分公式中可以看到,在计算yk+1时,其右端函数中 也含有yk+1,这种公式称为隐式公式,不能靠自身解决,需 要采用迭代方法来启动,称之为多步法。 其基本处理方法就是采用欧拉公式进行预报,采用梯形公式 进行校正,即