
1.2一个简单的产品组合问题 现在,让我们的思维来一个飞跃。我们注意 到:平行移动点画线就可以实现增加利润的目的。 我们为什么不在可行域的范围内,尽量地平行移 动点画线,以实现增加利润的目的?如果那样做, 最终,我们将得到利润最大的点A=60,C=30。它 位于直线20A+30C=2100上。这可以在图1-4上看 到。注意:尽管Coso的利润较高,我们只生产 了30台,而不是50台。从直观上看,这就是最优 解。事实也是如此 18
18 1.2 一个简单的产品组合问题 现在,让我们的思维来一个飞跃。我们注意 到:平行移动点画线就可以实现增加利润的目的。 我们为什么不在可行域的范围内,尽量地平行移 动点画线,以实现增加利润的目的?如果那样做, 最终,我们将得到利润最大的点A=60,C=30。它 位于直线20A+30C=2100上。这可以在图1-4上看 到。注意:尽管Cosmo的利润较高,我们只生产 了30台,而不是50台。从直观上看,这就是最优 解。事实也是如此
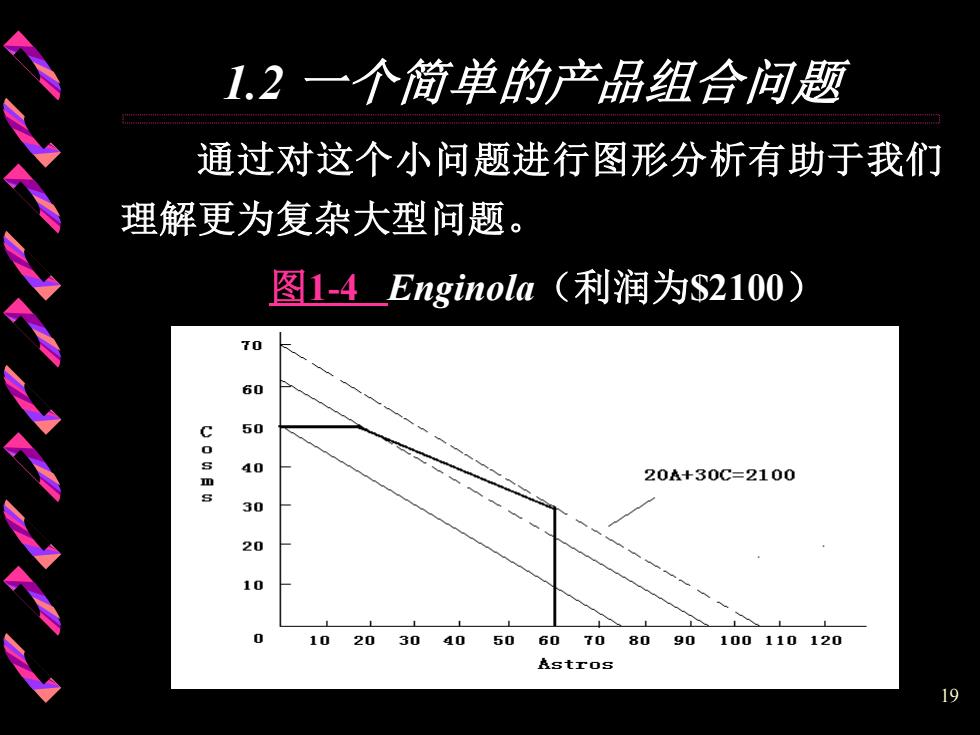
1.2一个简单的产品组合问题 通过对这个小问题进行图形分析有助于我们 理解更为复杂大型问题 。 图1-4 Enginola(利润为S2100) 70 60 g 50 40 20A+30C=2100 s 30 20 10 0 10 2030 40 50 6070 8090 100110120 Astros 19
19 1.2 一个简单的产品组合问题 通过对这个小问题进行图形分析有助于我们 理解更为复杂大型问题。 图1-4 Enginola(利润为$2100)

1.3线性概念 1.3线性概念 我们已经研究了一个例子。我们看到它是一 个线性数学规划,简称LP。与更一般的数学规划 相比较,线性规划更加容易求解。下面,我们对 线性概念作进一步研究 所谓线性规划就是所有活动变量(决策变量) 都是线性函数的数学规划。从应用角度来看,我 们认为线性概念有三个基本特征: 20
20 1.3 线性概念 1.3 线性概念 我们已经研究了一个例子。我们看到它是一 个线性数学规划,简称LP。与更一般的数学规划 相比较,线性规划更加容易求解。下面,我们对 线性概念作进一步研究。 所谓线性规划就是所有活动变量(决策变量) 都是线性函数的数学规划。从应用角度来看,我 们认为线性概念有三个基本特征:

.3线性概念 (1)比例性。单个变量(或活动) 自身的效果 是成比例的(例如,购买钢材的数量翻一翻,相 应的成本也翻一翻 (2)可加性。变量之间的相互作用具有可加性 (例如,销售总额等于钢产品和铝产品的销售额 之和) (③)连续性。变量必须是连续的。就是说变量 可以取分数值,例如6.38。对于一个变量,如果2 和3有意义,那么,2.51也有意义 21
21 1.3 线性概念 (1)比例性。单个变量(或活动)自身的效果 是成比例的(例如,购买钢材的数量翻一翻,相 应的成本也翻一翻)。 (2)可加性。变量之间的相互作用具有可加性 (例如,销售总额等于钢产品和铝产品的销售额 之和)。 (3)连续性。变量必须是连续的。就是说变量 可以取分数值,例如6.38。对于一个变量,如果2 和3有意义,那么,2.51也有意义

1.3线性概念 如果一个模型同时含有变量“销售价格”和 “销售数量”,那么这个模型或许就不是线性模 型。此时,比例性虽然得到满足,但是,两个变 量之间是相乘的关系而不是相加的关系。就是说, 销售总额=价格×数量,不是等于:价格+数量。 如果在购买商品的时候供应商给了折扣,这 时销售成本也不再满足比例性的要求(此时购买 钢材的成本要比按比例购买时的成本少一些) 22
22 1.3 线性概念 如果一个模型同时含有变量“销售价格”和 “销售数量” ,那么这个模型或许就不是线性模 型。此时,比例性虽然得到满足,但是,两个变 量之间是相乘的关系而不是相加的关系。就是说, 销售总额 = 价格×数量,不是等于:价格+数量。 如果在购买商品的时候供应商给了折扣,这 时销售成本也不再满足比例性的要求(此时购买 钢材的成本要比按比例购买时的成本少一些)