
第四章 目标规划 目标规划及其数学模型 目标规划的图解法 利用线性划求解目标规 划 3
3 第四章 目 标 规 划 目标规划及其数学模型 目标规划的图解法 利用线性规划求解目标规 划

第一节目标规划及其数学模型 目标规划问题的提出 应用线性规划,可以处理许多线性系统的最 优化问题。但是,线性规划作为一种决策工具, 在解决实际问题时,存在着一定的局限性。请看 下面的例子 例1某工厂生产两种产品,受到原材料供应 和设备工时的限制。在单件利润等有关数据已知 的条件下,要求制订出利润最大的生产计划。具 体数据见表4-1。 4
4 第一节 目标规划及其数学模型 一、目标规划问题的提出 应用线性规划,可以处理许多线性系统的最 优化问题。但是,线性规划作为一种决策工具, 在解决实际问题时,存在着—定的局限性。请看 下面的例子: 例1 某工厂生产两种产品,受到原材料供应 和设备工时的限制。在单件利润等有关数据已知 的条件下,要求制订出利润最大的生产计划。具 体数据见表4-1
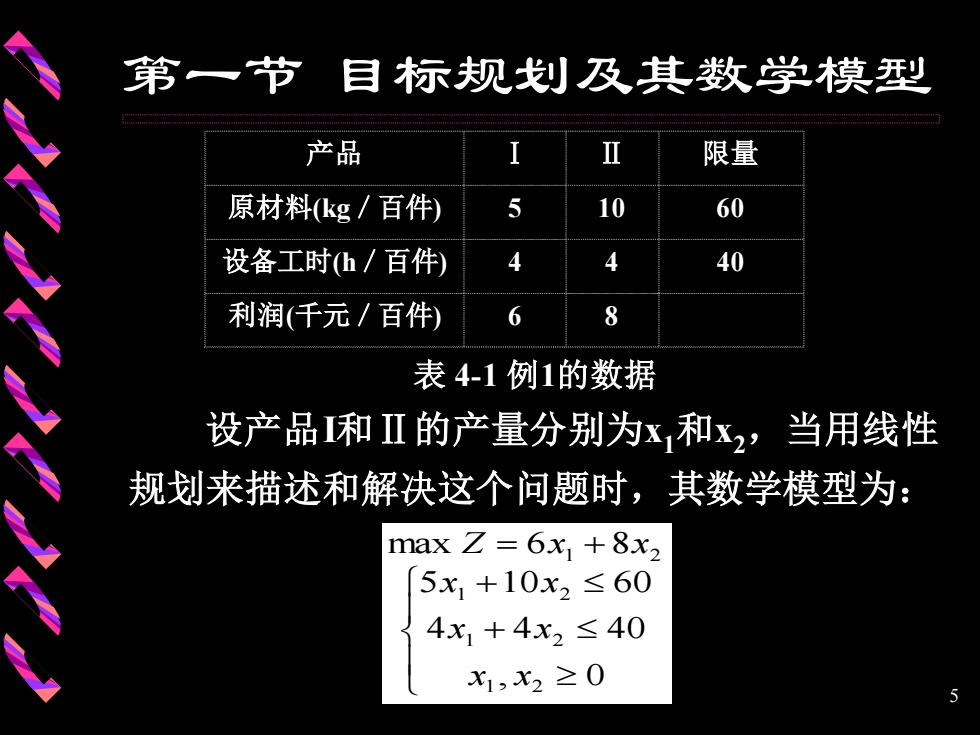
第一节目标规划及其数学模型 产品 限量 原材料kg/百件) 5 10 60 设备工时(h/百件) 4 4 40 利润(千元/百件) 6 8 表4-1例1的数据 设产品和Ⅱ的产量分别为x和x2,当用线性 规划来描述和解决这个问题时,其数学模型为: max Z=6x+8x2 5x1+10x2≤60 4x1+4x2≤40 x1,x2≥0 5
5 第一节 目标规划及其数学模型 表 4-1 例1的数据 产品 Ⅰ Ⅱ 限量 原材料(kg/百件) 5 10 60 设备工时(h/百件) 4 4 40 利润(千元/百件) 6 8 设产品I和Ⅱ的产量分别为x1和x2,当用线性 规划来描述和解决这个问题时,其数学模型为: + + = + , 0 4 4 40 5 10 60 max 6 8 1 2 1 2 1 2 1 2 x x x x x x Z x x

第一节目标规划及其数学模型 其最优解,即最优生产计划为x=8(百件) x2=2(百件),最大利润为64(千元) 从线性规划的角度来看,问题似乎已经得到 了圆满的解决。但是,如果站在厂计划人员的立 场上对此进行评价的话,问题就没这么简单了。 第一,这是一个单目标最优化问题。一般来 说,一个计划问题要满足多方面的要求。例如, 财务部门可能希望有尽可能大的利润,以实现其 年度利润目标。 6
6 第一节 目标规划及其数学模型 其最优解,即最优生产计划为x1 =8(百件), x2 =2(百件),最大利润为64(千元)。 从线性规划的角度来看,问题似乎已经得到 了圆满的解决。但是,如果站在厂计划人员的立 场上对此进行评价的话,问题就没这么简单了。 第一,这是一个单目标最优化问题。一般来 说,一个计划问题要满足多方面的要求。例如, 财务部门可能希望有尽可能大的利润,以实现其 年度利润目标

第一节目标规划及其数学模型 物资部门可能希望有尽可能小的物资消耗 以节约储备资金占用;销售部门可能希望产品品 种多样,适销对路;计划部门可能希望有尽可能 大的产品批量,便于安排生产等等。也就是说 一个计划问题实际上是一个多目标的决策问题 只是由于需要用线性规划来处理,计划人员才不 得不从众多目标要求中硬性选择其一,作为线性 规划的目标函数。 7
7 第一节 目标规划及其数学模型 物资部门可能希望有尽可能小的物资消耗, 以节约储备资金占用;销售部门可能希望产品品 种多样,适销对路;计划部门可能希望有尽可能 大的产品批量,便于安排生产等等。也就是说, 一个计划问题实际上是一个多目标的决策问题。 只是由于需要用线性规划来处理,计划人员才不 得不从众多目标要求中硬性选择其一,作为线性 规划的目标函数