
如果上述条件(1),3)不变,将2)改为(2): (2点集内包含边界上所有的点 这种平面点集称为平面闭区域, 如果一个区域可以被包围在一个以原点为圆心的某 个圆内,则称此区域为有界区域,否则称其为无界区域 例3,例5的定义域为有 界闭区域例4的定义域为无 界区域例6的定义域为有界 区域. 前页 后页 结束
前页 后页 结束 (2) 点集内包含边界上所有的点. 这种平面点集称为平面闭区域. 如果一个区域可以被包围在一个以原点为圆心的某 个圆内,则称此区域为有界区域,否则称其为无界区域. 例3,例5的定义域为有 界闭区域.例4的定义域为无 界区域.例6的定义域为有界 区域. 如果上述条件(1),(3)不变,将(2)改为 (2) :
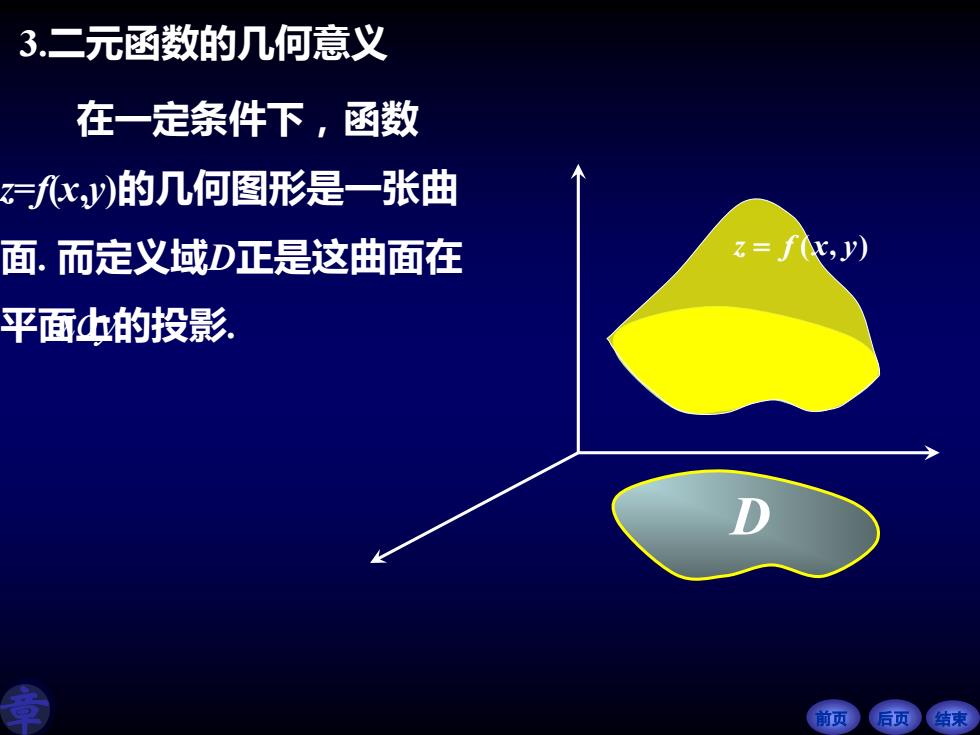
3.二元函数的几何意义 在一定条件下,函数 =cy)的几何图形是一张曲 面.而定义域D正是这曲面在 =f(x,y) 平面h的投影 前页后页结求
前页 后页 结束 3.二元函数的几何意义 在一定条件下,函数 z=f(x,y)的几何图形是一张曲 面. 而定义域D正是这曲面在 平面上的投影 xoy . D z f x y = ( , )

7.1.3二元函数的极限与连续 定义2设函数=fx,y)在点co)的某邻域有定义(点(xo) 可以除外),如果动点Pxy)以任意方式趋于定点化oo)时, 函数的对应值f化y)趋于一个确定数4,则称4为函数 =cy),当x→x,Jy→时的极限,记作 limf(x,y)=A, 或 lim f(x,y)=A, x→x0 (x,y)x0J%) y→y0 对于二元函数的极限存在,是指当Px,y)以任意方 式趋于定点P心,o),函数都无限接近于A. 当P化y)以不同路径趋于点P(x,)时,函数趋于不同的 值,则可以断定函数在该点的极限不存在
前页 后页 结束 7.1.3 二元函数的极限与连续 定义2 设函数z=f(x,y)在点(x0 ,y0 )的某邻域有定义(点(x0 ,y0 ) 可以除外),如果动点P(x,y) 以任意方式趋于定点(x0 ,y0 )时, 函数的对应值f (x,y)趋于一个确定数A,则称A为函数 z=f(x,y),当 x x y y → → 0 0 , 时的极限,记作 0 0 lim ( , ) , x x y y f x y A → → = 0 0 ( , ) ( , ) lim ( , ) , x y x y f x y A → 或 = 对于二元函数的极限存在,是指当P(x,y)以任意方 式趋于定点P0 (x0 , y0 ),函数都无限接近于A. 值,则可以断定函数在该点的极限不存在. 当P(x,y)以不同路径趋于点 P x y ( , ) 0 0 时,函数趋于不同的

。x2+y2≠0, 例7讨论二元函数f(x,y)=了 x2+y2=0 当Pcy)→O0,0)时,极限是否存在. 解当Pxy)沿轴趋于点00,0)即=0时,fx,y=f心,0)=0 (≠0),∴.l1imf(x,0)=0. x->0 当P心y)沿轴趋于点O0,0)即x=0时, xy)=f0,y=00≠0), ∴.limf(0,y)=0. y>0 当Pcy)沿直线=kx轴趋于点O0,0)时, 前 后页结束
前页 后页 结束 例7 讨论二元函数 + = + = + 0, 0 , 0 ( , ) 2 2 2 2 2 2 x y x y x y xy f x y , 当P(x,y)→O(0,0)时,极限是否存在. 解 当P(x,y)沿x轴趋于点O(0,0)即y=0时,f(x,y)=f(x,0)=0 (x≠0), lim ( ,0) 0. 0 = → f x x 当P(x,y)沿y轴趋于点O(0,0)即x=0时, f(x,y)=f(0,y)=0(y≠0), lim (0, ) 0. 0 = → f y y 当P(x,y)沿直线y=k x轴趋于点O(0,0)时

当P化,y)沿直线=kx轴趋于点O0,0)时, 即x,y片x,kx尸 1+ 2(x0) ∴.limf(x,y)=lim, y=kx x01+k21+k x→0 其极限值随直线斜率的不同而不同. 因此1imf(x,y)不存在, x→0 y'-→0 一元函数极限的有些运算法则(如四则运算法则, 夹逼定理等)可以相应地推广到二元函数 前页
前页 后页 结束 2 2 , 0 0 1 1 lim ( , ) lim k k k k f x y x x y kx + = + = → → = 即f(x,y)=f(x,kx)= ( 2 x≠0), 1 k k + 其极限值随直线斜率k的不同而不同. 因此 lim ( , ) 不存在. 0 0 f x y y x → → 一元函数极限的有些运算法则(如四则运算法则, 夹逼定理等) 可以相应地推广到二元函数. 当P(x,y)沿直线y=k x轴趋于点O(0,0)时