
N/2仍为偶数,进一步分解:N/2W/4 x(21)=x,() 1=0,1,.,W/4-1 x(21+1)=x4() X,(E)=X()+W2X4(k) K低+等-x-x因 k=0,1 x3(0)=x1(0)=x(0) X3(0) 点 X1(0) 4 DFT X3(1) x3(1)=x1(2)=x(4)° 才X(I) x4(0)=x1(1)=x(2) X4(0) X(2) x4(1)=x1(3)=x(6)— DFT X4(1) X(3) N/2 图4-3由两个N/4点DFT组合成一个N/2点DFT
1 3 1 4 (2 ) ( ) (2 1) ( ) x l x l x l x l l N 0,1,..., / 4 1 1 3 / 2 4 1 3 / 2 4 ( ) ( ) ( ) ( ) ( ) ( ) 4 k N k N X k X k W X k N X k X k W X k 0,1,..., 1 4 N k N / 2仍为偶数,进一步分解:N / 2 N / 4

同理: X(K)=X()+W2X(k) X,k+)=X,()-W2X, k=01-1 其中: Xs(k)=DFT[xs()]=DFT[x2 (21)] 1=0,1,N/4-1 X(k)=DFT[x()]=DFT[x,(21+1)] 统一系数:W2→W
2 5 / 2 6 2 5 / 2 6 ( ) ( ) ( ) ( ) ( ) ( ) 4 k N k N X k X k W X k N X k X k W X k 0,1,..., 1 4 N k 同理: 其中: 5 5 2 X k DFT x l DFT x l ( ) [ ( )] [ (2 )] 6 6 2 X k DFT x l DFT x l ( ) [ ( )] [ (2 1)] l N 0,1,..., / 4 1 2 / 2 k k 统一系数:W W N N

X3(0) X(0) x3(0)=x1(0)=x(0)— 点 X(0) DFT X(1) X(1) x3(1)=x1(2)=x(4) X4(0) X1(2) x4(0)=x1(1)=x(2) 点 咽 DFT X4(1) X(3) x4(1)=x1(3)=x(6) X(3) 味 -1 xs(0)=x2(0)=x(1) Xs(0) X(0) WN xs(1)=x2(2)=x(5) DFT X(1) X(1) x6(0)=x2(1)=x(3) X6(0) X(2) R X(6) -1 x6(1)=x2(3)=x(7) DET X6(1) X(3) X(7) W子 -1 W 图4-4按时间抽选,将一个N点DFT分解为四个N4点DFTN=8)

这样逐级分解,直到2点DFT 当N=8时,即分解到X(k),X4(),X(), X(),k=0,1 N/4-1 X,)=∑x0m4=∑x0w4 k=0,1 1=0 1=0 X,(0)=x,(0)W+Wx,(1)=x(0)+W8x(4) X3(1)=x,(0)W+Wx(1)=x(0)-W8x(4) X,因=Σx0w-∑x0w N/4-1 k=0,1 1=0 1=0 X4(0)=x4(O)W+Wx4(1)=x(2)+W0x(6) X(1)=x,(0)W+Wx,()=x(2)-Wx(6)
这样逐级分解,直到2点DFT 当N = 8时,即分解到X3 (k),X4 (k),X5 (k), X6 (k),k = 0, 1 0 0 0 3 3 2 2 3 0 1 0 3 3 2 2 3 (0) (0) (1) (0) (4) (1) (0) (1) (0) (4) N N X x W W x x W x X x W W x x W x / 4 1 1 3 3 / 4 3 / 4 0 0 ( ) ( ) ( ) N lk lk N N l l X k x l W x l W k 0,1 0 0 0 4 4 2 2 4 0 1 0 4 4 2 2 4 (0) (0) (1) (2) (6) (1) (0) (1) (2) (6) N N X x W W x x W x X x W W x x W x / 4 1 1 4 4 / 4 4 / 4 0 0 ( ) ( ) ( ) N lk lk N N l l X k x l W x l W k 0,1
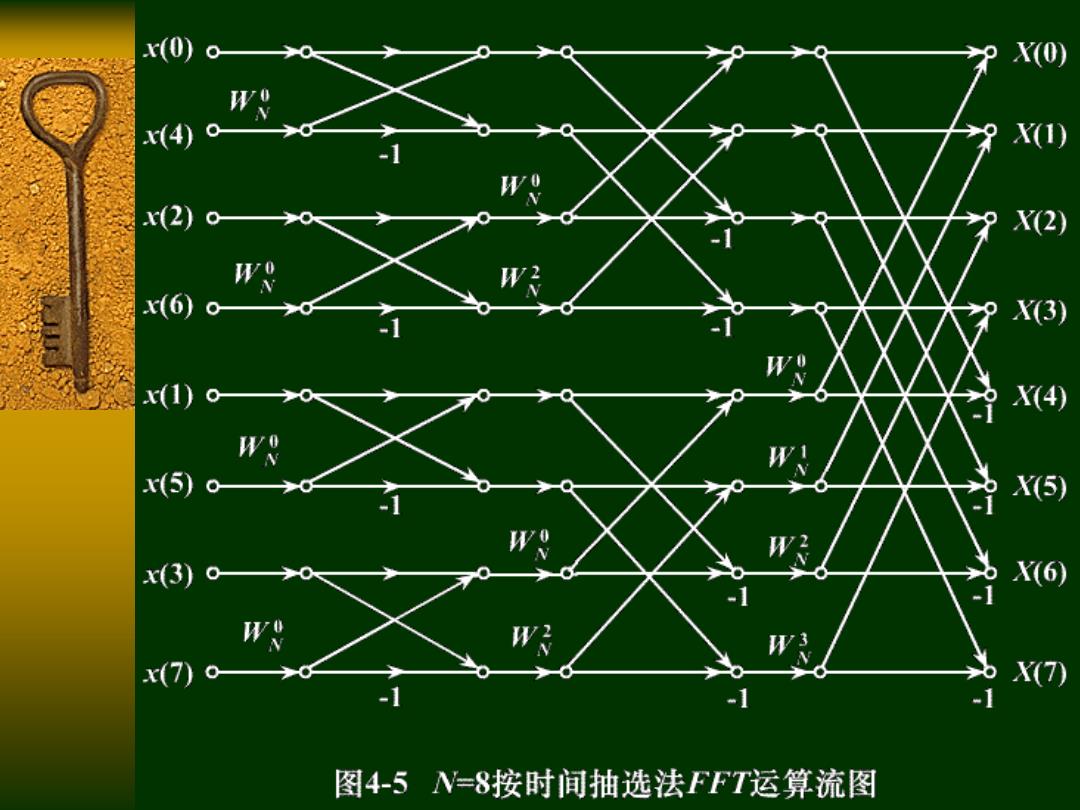
x(0)o X(0) W x(4) 0 x(2) WN x(6) x(1) x(5) x(3)o x(7)- -1 -1 1 图4-5N=8按时间抽选法FFT运算流图