
3.转动惯量 4.引力 具体要求:会用重积分计算一些几何量和物理量。 第二十二章曲面积分 重点:两类曲面积分的计算与性质: 难点:两类曲面积分的联系,高斯公式与斯托克斯公式。 第一节第一型曲面积分 1.第一型曲面积分的概念 2.第一型曲面积分的计算 具体要求:理解第一型曲面积分的定义,掌握第一型曲面积分的计算。 第二节第二型曲面积分 1.曲面的侧 2.第二型曲面积分的概念 3.第二型曲面积分的计算 4.两类曲面积分的联系 具体要求:理解第二型曲面积分的定义,掌握第二型曲面积分的计算,会进行两类曲面积分之 间的转换。 第三节高斯公式与斯托克斯公式 1. 高斯公式 2.斯托克斯公式 具体要求:理解高斯公式与斯托克斯公式,并会用高斯公式与斯托克斯公式计算第二型曲面积 分与空间第二型曲线积分:知道空间曲线积分与路线无关的条件,会求全微分的原函数。 第四节场论初步 1.场的概念 2.梯度场、散度场、旋度场简介 具体要求:了解梯度场、散度场、旋度场的概念以及相互之间的关系。 (二)教学方法与手段 主要采取课堂讲授式教学,习题课、课外辅导为辅。注意引导启发学生:使用板书加多媒体课件。 六、学时分配 教学内容 各教学环节学时分配 作业 题量 备注 讲 实 实 课 讨 习 小 章节 主要内容 授 验 训 外 论 题 计
15 3. 转动惯量 4. 引力 具体要求:会用重积分计算一些几何量和物理量。 第二十二章 曲面积分 重点:两类曲面积分的计算与性质; 难点:两类曲面积分的联系,高斯公式与斯托克斯公式。 第一节 第一型曲面积分 1. 第一型曲面积分的概念 2. 第一型曲面积分的计算 具体要求:理解第一型曲面积分的定义,掌握第一型曲面积分的计算。 第二节 第二型曲面积分 1. 曲面的侧 2. 第二型曲面积分的概念 3. 第二型曲面积分的计算 4. 两类曲面积分的联系 具体要求:理解第二型曲面积分的定义,掌握第二型曲面积分的计算,会进行两类曲面积分之 间的转换。 第三节 高斯公式与斯托克斯公式 1. 高斯公式 2. 斯托克斯公式 具体要求:理解高斯公式与斯托克斯公式,并会用高斯公式与斯托克斯公式计算第二型曲面积 分与空间第二型曲线积分;知道空间曲线积分与路线无关的条件,会求全微分的原函数。 第四节 场论初步 1. 场的概念 2. 梯度场、散度场、旋度场简介 具体要求:了解梯度场、散度场、旋度场的概念以及相互之间的关系。 (二)教学方法与手段 主要采取课堂讲授式教学,习题课、课外辅导为辅。注意引导启发学生;使用板书加多媒体课件。 六、学时分配 教学内容 各教学环节学时分配 作业 题量 备注 章节 主要内容 讲 授 实 验 实 训 课 外 讨 论 习 题 小 计
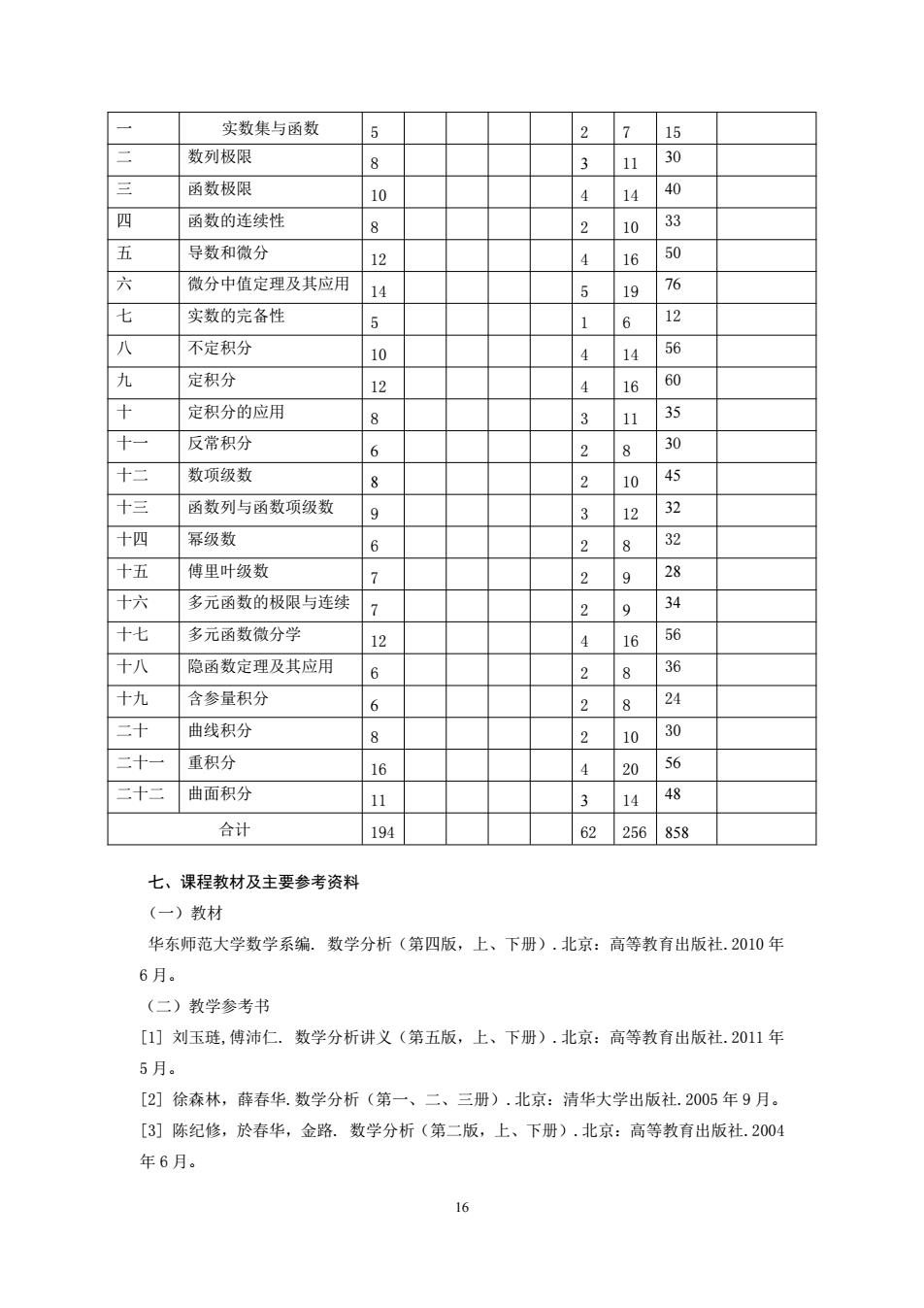
实数集与函数 5 2 15 数列极限 8 3 11 30 三 函数极限 10 4 14 40 四 函数的连续性 8 2 10 33 五 导数和微分 12 4 16 50 六 微分中值定理及其应用 14 5 19 76 七 实数的完备性 5 1 6 12 八 不定积分 10 4 14 56 九 定积分 12 4 16 60 十 定积分的应用 8 3 11 35 十一 反常积分 6 2 8 30 十二 数项级数 8 2 10 45 十三 函数列与函数项级数 9 12 32 十四 幂级数 6 2 8 32 十五 傅里叶级数 7 2 9 28 十六 多元函数的极限与连续 7 2 9 34 十七 多元函数微分学 12 4 16 56 十八 隐函数定理及其应用 6 2 8 36 十九 含参量积分 6 2 8 24 二十 曲线积分 P 2 10 30 二十一 重积分 16 20 56 二十二 曲面积分 11 3 14 48 合计 194 62 256 858 七、课程教材及主要参考资料 (一)教材 华东师范大学数学系编。数学分析(第四版,上、下册).北京:高等教育出版社.2010年 6月。 (二)教学参考书 [1]刘玉琏,傅沛仁.数学分析讲义(第五版,上、下册).北京:高等教育出版社.2011年 5月。 [2]徐森林,薛春华.数学分析(第一、二、三册).北京:清华大学出版社.2005年9月。 [3]陈纪修,於春华,金路.数学分析(第二版,上、下册).北京:高等教育出版社.2004 年6月。 16
16 一 实数集与函数 5 2 7 15 二 数列极限 8 3 11 30 三 函数极限 10 4 14 40 四 函数的连续性 8 2 10 33 五 导数和微分 12 4 16 50 六 微分中值定理及其应用 14 5 19 76 七 实数的完备性 5 1 6 12 八 不定积分 10 4 14 56 九 定积分 12 4 16 60 十 定积分的应用 8 3 11 35 十一 反常积分 6 2 8 30 十二 数项级数 8 2 10 45 十三 函数列与函数项级数 9 3 12 32 十四 幂级数 6 2 8 32 十五 傅里叶级数 7 2 9 28 十六 多元函数的极限与连续 7 2 9 34 十七 多元函数微分学 12 4 16 56 十八 隐函数定理及其应用 6 2 8 36 十九 含参量积分 6 2 8 24 二十 曲线积分 8 2 10 30 二十一 重积分 16 4 20 56 二十二 曲面积分 11 3 14 48 合计 194 62 256 858 七、课程教材及主要参考资料 (一)教材 华东师范大学数学系编. 数学分析(第四版,上、下册).北京:高等教育出版社.2010 年 6 月。 (二)教学参考书 [1] 刘玉琏,傅沛仁. 数学分析讲义(第五版,上、下册).北京:高等教育出版社.2011 年 5 月。 [2] 徐森林,薛春华.数学分析(第一、二、三册).北京:清华大学出版社.2005 年 9 月。 [3] 陈纪修,於春华,金路. 数学分析(第二版,上、下册).北京:高等教育出版社.2004 年 6 月

[4]邝荣雨,杨新华,林莉.数学分析题集.北京:教育科学出版社.1997年7月。 八、其他说明 教学内容相符情况下,可更换较新的更优秀的教材。 17
17 [4] 邝荣雨,杨新华,林莉. 数学分析题集.北京:教育科学出版社.1997 年 7 月。 八、其他说明 教学内容相符情况下,可更换较新的更优秀的教材

《高等代数》课程教学大纲 (Higher Algebra) 执笔者:胡永忠 审核人:黄国顺 编写日期:2017年9月 一、课程基本信息 适用专业 适用于数学与应用数学 开课单位 数学与大数据学院 课程类型 专业教育类(专业基础课) 课程性质 必修 是否为双语 否 学分数 9学分 学时数 总学时144,其中:实验(实训)0学时:课外0学时 先修课程 无 后续课程 常微分方程、数学模型、运筹学、数值分析、近世代数等 二、课程简述 《高等代数》是高等院校数学专业的一门重要的基础课,其主要任务是使学生获得数学 的基本思想方法和多项式理论、行列式、线性方程组、矩阵论、向量空间、线性变换、欧氏 空间和酉空间、二次型等方面的系统知识。它一方面为后继课程(如近世代数、数论、离散 数学、计算方法、微分方程、泛函分析)提供一些所需的基础理论和知识。尤其在本世纪, 计算机技术、通讯信息技术和现代生物工程技术已成为最热门的学科领域,这些学科均需要 代数学的发展。 《高等代数》是中学代数的继续和提高。通过这一课程的教学,应使学生掌握为进一步 提高专业知识水平所必需的代数基础理论和基本方法,且对初等代数内容有比较深入的了解, 并能居高临下地处理中学数学的有关教材,培养学生独立思考、科学抽象思维、正确的逻辑 推断能力和迅速准确的运算能力,对开发学生智能、加强“三基”(基础知识、基本理论、 基本理论)及培养学生创造能力、树立辩证唯物论观点等有重要的作用。 三、本课程所支撑的毕业要求 18
18 《高等代数》课程教学大纲 (Higher Algebra) 执 笔 者:胡永忠 审 核 人:黄国顺 编写日期:2017 年 9 月 一、课程基本信息 适用专业 适用于数学与应用数学 开课单位 数学与大数据学院 课程类型 专业教育类(专业基础课) 课程性质 必修 是否为双语 否 学分数 9 学分 学时数 总学时 144 ,其中:实验(实训) 0 学时 ;课外 0 学时 先修课程 无 后续课程 常微分方程、数学模型、运筹学、数值分析、近世代数等 二、课程简述 《高等代数》是高等院校数学专业的一门重要的基础课,其主要任务是使学生获得数学 的基本思想方法和多项式理论、行列式、线性方程组、矩阵论、向量空间、线性变换、欧氏 空间和酉空间、二次型等方面的系统知识。它一方面为后继课程(如近世代数、数论、离散 数学、计算方法、微分方程、泛函分析)提供一些所需的基础理论和知识。尤其在本世纪, 计算机技术、通讯信息技术和现代生物工程技术已成为最热门的学科领域,这些学科均需要 代数学的发展。 《高等代数》是中学代数的继续和提高。通过这一课程的教学,应使学生掌握为进一步 提高专业知识水平所必需的代数基础理论和基本方法,且对初等代数内容有比较深入的了解, 并能居高临下地处理中学数学的有关教材,培养学生独立思考、科学抽象思维、正确的逻辑 推断能力和迅速准确的运算能力,对开发学生智能、加强“三基”(基础知识、基本理论、 基本理论)及培养学生创造能力、树立辩证唯物论观点等有重要的作用。 三、本课程所支撑的毕业要求

本课程所支撑(达成)的毕业要求 毕业要求 指标点 毕业要求2:具有扎实的数学学科知识,掌握数学 应用的基本方法,具有良好的数学思维,受到现 指标2-1:具有扎实的数学学 代数学教育基本理论和基本技能的训练,具有独 科知识,掌握数学应用的基本 立组织数学教学、班级管理和科学研究的工作能 方法。 力。 指标2-2:具有良好的数学思 维,受到现代数学教育基本理 论和基本技能的训练。 四、考核方式及成绩评定 (一)考核目标 考核学生对本课程知识体系的掌握程度。 (二)考核方式 本课程以期末考试结合平时成绩来考核。 (三)成绩评定 总评成绩由平时成绩和期末考试成绩组成,平时成绩占30%,期末考试成绩占70%。 五、课程内容、重点和难点及教学方法与手段 (一)课程内容、重点和难点 第一章多项式 重点:整除,最大公因式,互素,标准分解式,代数基本定理,整系数多项式的有理根, Eisenstein判别法。 难点:整除,最大公因式,整系数多项式的有理根,Eisenstein判别法。 第一节数域 一、讲授内容 1.数的代数性质 2.数域的定义 二、具体要求 1.能根据定义判断给定数集是否数域 第二节一元多项式 一、讲授内容 19
19 本课程所支撑(达成)的毕业要求 毕业要求 指标点 毕业要求 2:具有扎实的数学学科知识,掌握数学 应用的基本方法,具有良好的数学思维,受到现 代数学教育基本理论和基本技能的训练,具有独 立组织数学教学、班级管理和科学研究的工作能 力。 指标 2-1:具有扎实的数学学 科知识,掌握数学应用的基本 方法。 指标 2-2:具有良好的数学思 维,受到现代数学教育基本理 论和基本技能的训练。 四、考核方式及成绩评定 (一)考核目标 考核学生对本课程知识体系的掌握程度。 (二)考核方式 本课程以期末考试结合平时成绩来考核。 (三)成绩评定 总评成绩由平时成绩和期末考试成绩组成,平时成绩占 30%,期末考试成绩占 70%。 五、课程内容、重点和难点及教学方法与手段 (一)课程内容、重点和难点 第一章 多项式 第一节 数域 一、讲授内容 1. 数的代数性质 2. 数域的定义 二、具体要求 1.能根据定义判断给定数集是否数域 第二节 一元多项式 一、讲授内容 重点:整除,最大公因式,互素,标准分解式,代数基本定理,整系数多项式的有理根, Eisenstein 判别法。 难点:整除,最大公因式,整系数多项式的有理根,Eisenstein 判别法