
2016/4/6 Example 12.2 Take E/and /as constants. 16 n 输月冷大学 目土本2程学税 16 Candy distribution:review Gamel 0 8 8 4 6 5 5 6 包同冷大学 目土本2程幸悦 6
2016/4/6 6 Example 12.2 A B C 16 D Take EI and l as constants. 3*y=16 y=? Candy distribution: review 16 0 8 8 4 4 8 4 6 6 5 5 6 Game!
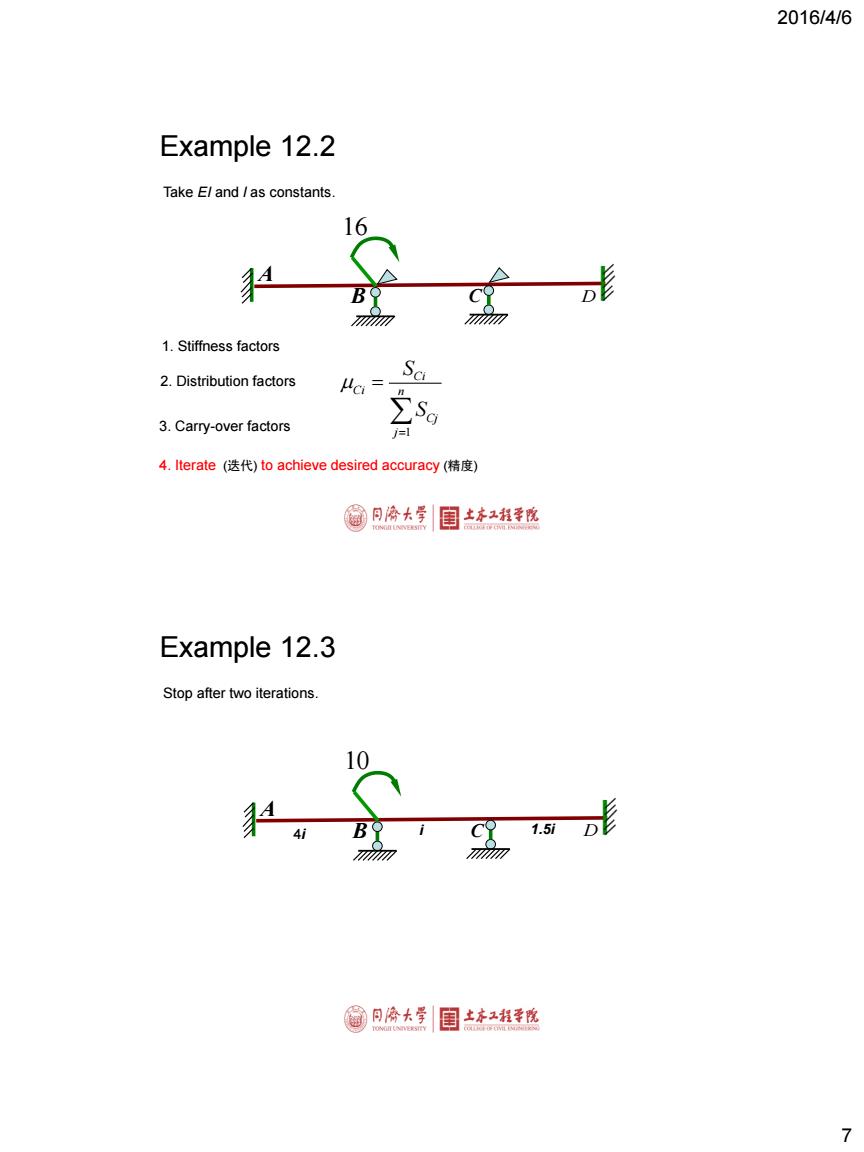
2016/4/6 Example 12.2 Take E/and /as constants. 16 1.Stiffness factors 2.Distribution factors 3.Carry-over factors i=1 4.Iterate(迭代)to achieve desired accuracy(精度) 月冷大学 国土本2程季悦 Example 12.3 Stop after two iterations. 10 41 1.5i D形 国月冷大学 目土本2程幸院 >
2016/4/6 7 Example 12.2 A B C 16 D Take EI and l as constants. 1 Ci Ci n Cj j S S 1. Stiffness factors 2. Distribution factors 3. Carry-over factors 4. Iterate (迭代) to achieve desired accuracy (精度) Example 12.3 A B C 10 4i i 1.5i D Stop after two iterations

2016/4/6 Unbalanced moment due to in-span loading (跨间荷载导致的不平衡弯矩) The negative value of total fixed end moments at the joint is to be distributed. P2 MR+M女9a品 Mc4=M×44+Ma McB=M×4B+MEB MAc MX Hc xCc+Mic MBc M X HcB XCcB+MBc CB 输问冷大学 国土本2相学悦 Factors for different boundary conditions: (不同边界条件下的系数取值) Stiffness factors SAj SAB=4i SAn=3i A B i B Distribution factors MAj ΣS i=1 A Carry-over factors CAj AB=1/2 AB =0 AB A 包向傍大学 目土本工程学院 8
2016/4/6 8 F MCA M CA MCA F MCB M CB MCB R1P C F MCB F MCA ( ) 1 F F M R P MCA MCB Z1 1 A B 1i 2 C i 1 4i 2 3i 1 2i A B 1 l 2 l 1 1 1 i EI / l 2 2 2 C i EI / l FP1 FP2 F MAC M CA CCA MAC F MBC M CB CCB MBC Unbalanced moment due to in-span loading (跨间荷载导致的不平衡弯矩) R1P C M The negative value of total fixed end moments at the joint is to be distributed. Factors for different boundary conditions: (不同边界条件下的系数取值) A B S i AB 4 i A B S i AB 3 i A B S i AB i Distribution factors Aj Carry-over factors CAj n j Aj Ai Ai S S 1 A B CAB 1/ 2 i A B CAB 0 i A B CAB 1 i Stiffness factors SAj