
§1运输问颗的典例和数学模型 学习要点: 1.掌握运输问题模型结构; 2.了解运输问题模型特点
学习要点: 1.掌握运输问题模型结构; 2.了解运输问题模型特点。 §1 运输问题的典例和数学模型

§2表上作业法 表上作业法是一种求解运输问题的特殊方法,其实质是单 纯形法。 步骤 描述 方法 第一步 求初始基本可行解(初始调运方案) 最小元素法、 元素差额法、 求检验数并判断是否得到最优解当非基变 闭回路法和位 第二步 量的检验数σ全都非负时得到最优解,若 存在检验数σ,<0,说明还没有达到最优, 势法 转第三步。 调整运量,即换基,选一个变量出基,对 第三步 原运量进行调整得到新的基可行解,转入 第二步
§2 表上作业法 表上作业法是一种求解运输问题的特殊方法,其实质是单 纯形法。 步骤 描述 方法 第一步 求初始基本可行解(初始调运方案) 最小元素法、 元素差额法、 第二步 求检验数并判断是否得到最优解当非基变 量的检验数σij全都非负时得到最优解,若 存在检验数σij <0,说明还没有达到最优, 转第三步。 闭回路法和位 势法 第三步 调整运量,即换基,选一个变量出基,对 原运量进行调整得到新的基可行解,转入 第二步
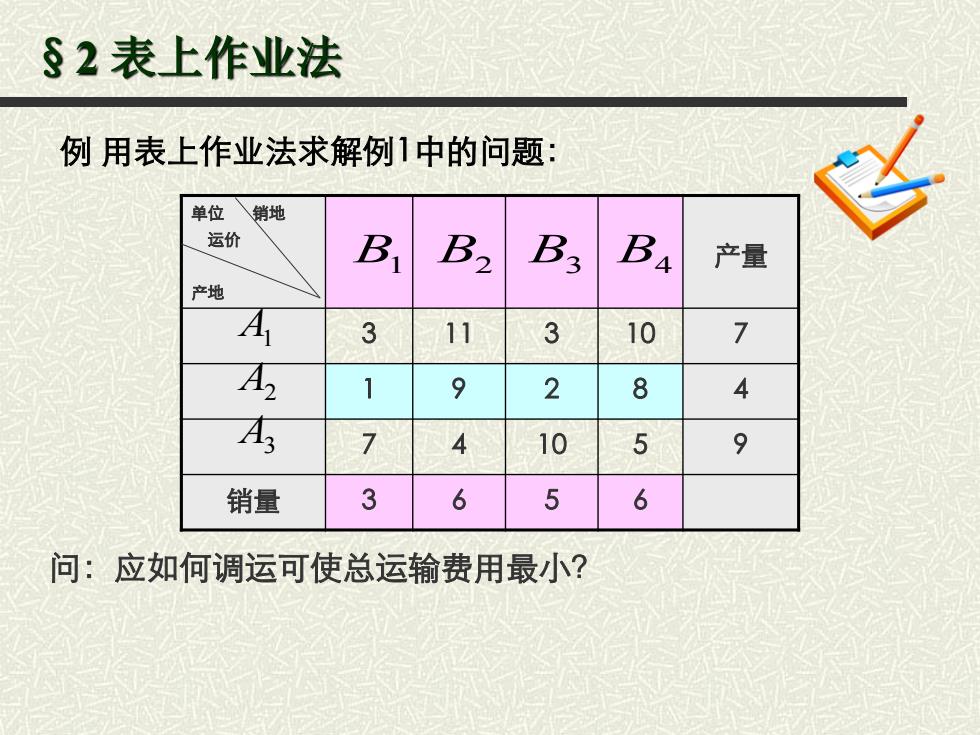
§2表上作业法 例用表上作业法求解例1中的问题: 单位销地 运价 B B2 B3 B 产量 产地 A 3 11 3 10 7 西 1 9 2 8 4 4 10 5 9 销量 3 6 5 6 问:应如何调运可使总运输费用最小?
§2 表上作业法 例 用表上作业法求解例1中的问题: 单位 销地 运价 产地 产量 3 11 3 10 7 1 9 2 8 4 7 4 10 5 9 销量 3 6 5 6 1 2 3 4 B B B B 3 2 1 A A A 问:应如何调运可使总运输费用最小?
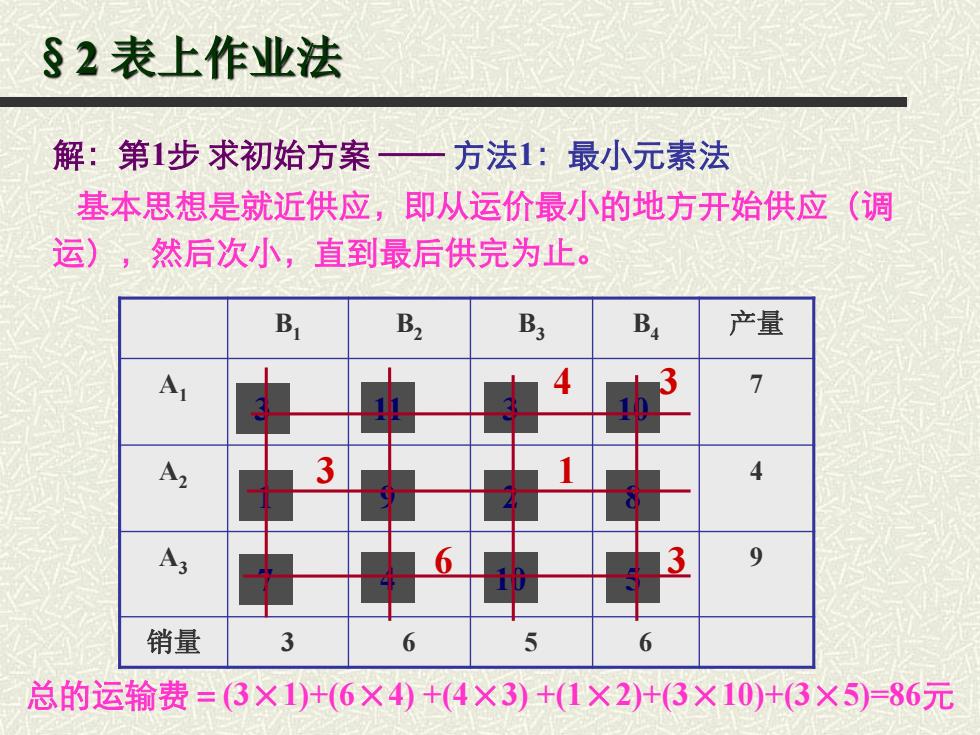
§2表上作业法 解:第1步求初始方案一 方法1:最小元素法 基本思想是就近供应,即从运价最小的地方开始供应(调 运),然后次小,直到最后供完为止。 B B2 B 产量 A 7 3 4 A3 9 销量 3 6 5 6 总的运输费=3×1)+(6×4)+(4×3)+(1×2)+(3×10)+(3×5)=86元
§2 表上作业法 解:第1步 求初始方案 —— 方法1:最小元素法 基本思想是就近供应,即从运价最小的地方开始供应(调 运),然后次小,直到最后供完为止。 B1 B2 B3 B4 产量 A1 7 A2 4 A3 9 销量 3 6 5 6 3 11 3 10 1 9 2 7 4 10 5 8 3 4 1 6 3 3 总的运输费=(3×1)+(6×4) +(4×3) +(1×2)+(3×10)+(3×5)=86元
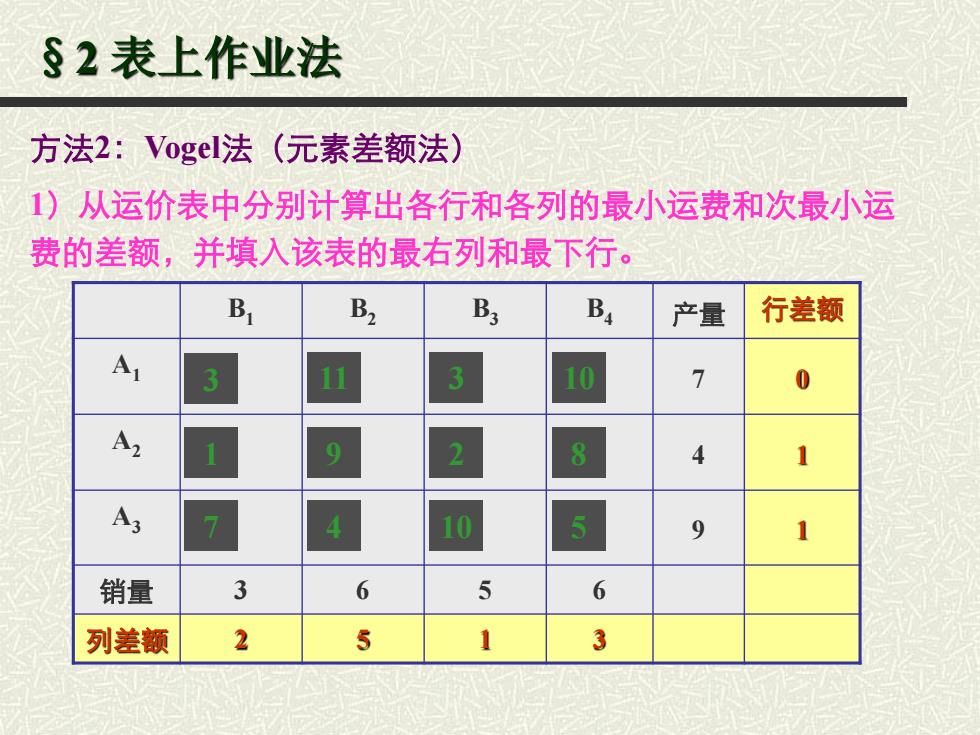
§2表上作业法 方法2:Vogel法(元素差额法) 1)从运价表中分别计算出各行和各列的最小运费和次最小运 费的差额,并填入该表的最右列和最下行。 Br B2 B B 产量 行差额 11 10 7 A2 2 8 A3 10 5 9 销量 3 6 5 6 列差额 2 5 3
§2 表上作业法 方法2:Vogel法(元素差额法) 1)从运价表中分别计算出各行和各列的最小运费和次最小运 费的差额,并填入该表的最右列和最下行。 B1 B2 B3 B4 产量 行差额 A1 7 0 A2 4 1 A3 9 1 销量 3 6 5 6 列差额 2 5 1 3 3 11 3 10 1 9 2 7 4 10 5 8