
弯曲变形共车轭梁实梁虚梁力边界支承和端部情况位移边界相应的支承和端部情况r-oM. -0固定端A自由端A0.-0,-0f-oM 0固定端A自由端A0, *00.0-oM. -04铰支端A铰支端A0.-00. 0-oM.-0A中间铰中间铰A支座A0A左=04右-0Q左-Q佑右±0于A左-f A右MA左-MA右A中间铰A中间铰①A左+0A右0A左+0/右支座A
中间铰 支座 A 实 梁 虚 梁 共 轭 梁 支 承 和 端 部 情 况 位移边界 力边界 相应的支承和端部情况 fA=0 A=0 fA0 A0 A左 A右 f A左= f A右 MA左=MA右 QA左QA右 固定端A A M A = 0 QA = 0 M A 0 QA 0 M A = 0 QA 0 fA =0 A 0 左 = 右 0 A A fA =0 左 = 右 0 QA QA M A = 0 固定端A A 自由端A A 自由端A A 铰支端A A 铰支端A A 中间铰 支座 A 中间铰A 中间铰A

弯曲变形总结:等截面实梁与虚梁的关系如下:②几何形状完全相同。1x轴指向及坐标原点完全相同。③令:g(x)=-M(x)依此建立虚梁上的分布载荷。④依实梁的“位移”边界条件,建立虚梁的“力”边界条件α:固定端→自由端EIf -M ,EI0 -Q.b:铰支座→铰支座c:中间铰支座 中间铰链③依虚梁的“内力”,求实梁的“位移”M..,Qxf.EIEI
总结:等截面实梁与虚梁的关系如下: ① x 轴指向及坐标原点完全相同。 ②几何形状完全相同。 ④依实梁的“位移”边界条件,建立虚梁的“力”边界条件。 EIf A =M A EI A =QA ; EI Q EI M f x x x x = ; = ⑤依虚梁的“内力”,求实梁的“位移”。 a :固定端 自由端 b :铰支座 铰支座 c :中间铰支座 中间铰链 ③ 令: q(x) = −M (x)依此建立虚梁上的分布载荷

弯曲变形例2求下列等截面直梁B点的位移(挠度和转角)。q解:建立坐标和虚梁1e求实梁的弯矩方程x福以确定虚梁荷载M(x)=-I(L-x)2qL =q(x) --M(x) -(L-x)22q(x)②求虚梁B点的剪力和弯矩,B以求实梁B点的转角和挠度
解: 建立坐标和虚梁 例2 求下列等截面直梁B点的位移(挠度和转角)。 求虚梁B点的剪力和弯矩, 以求实梁B点的转角和挠度 求实梁的弯矩方程 以确定虚梁荷载 2 ( ) 2 q M (x) = − L − x 2 ( ) 2 q q(x) = −M (x) = L − x q L A B f x 2 2 0 qL q = q(x) A B L
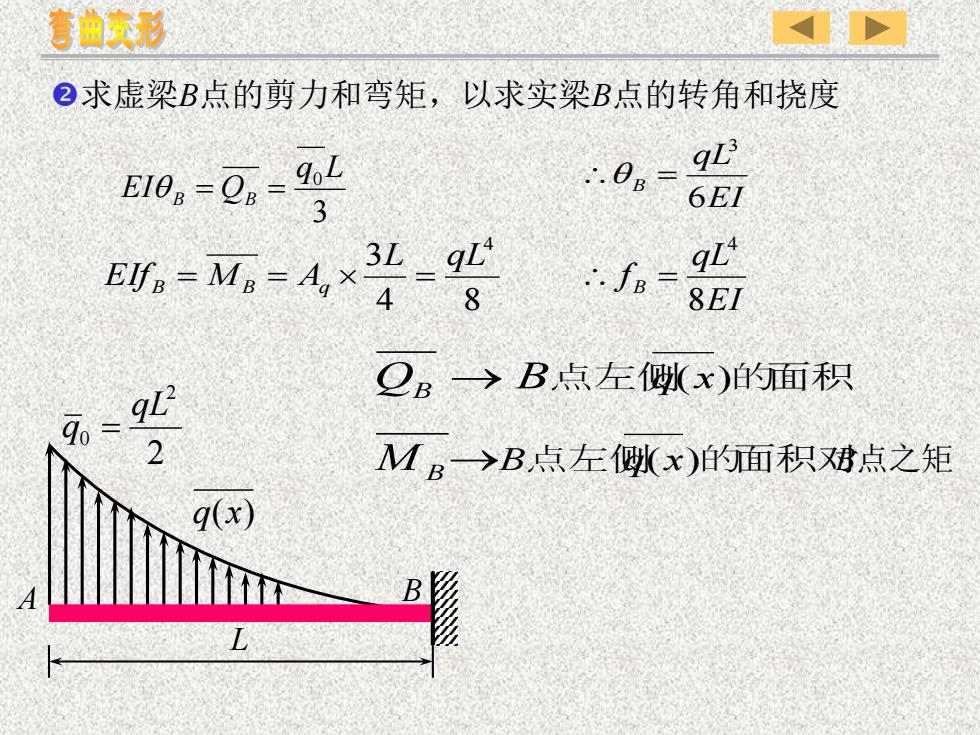
弯曲变形②求虚梁B点的剪力和弯矩,以求实梁B点的转角和挠度qL3..0.-E10 -0, - 9oL6EI3qL43L -qL4.. fs =.EIf。- M.=A,×848EIQ一→B点左侧(x)的面积qL?qo2MB→>B点左侧(x)的面积戏点之矩q(x)B
求虚梁B点的剪力和弯矩,以求实梁B点的转角和挠度 3 q0 L EI B = QB = 4 8 3 4 L qL EIfB = MB = Aq = EI qL B 6 3 = EI qL f B 8 4 = QB → B点左侧q(x)的面积 2 2 0 qL q = q(x) A B L MB →B点左侧q(x)的面积对 B点之矩